Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Approximate a parametric surface with different graphics primitives
ResourceFunction["ApproximatedSurface"][surf,{u,u0,uf,m},{v,v0,vf,n},"prim"] compute m×n points of a parametric surface varying u from u0 to uf and v from v0 to vf using graphics primitives of the type "prim". | |
ResourceFunction["ApproximatedSurface"][surf,{u,u0,uf,m},{v,v0,vf,n},{"prim",c1,c2}] compute the parametric surface varying a parameters c1 and c2, when available. |
| "Coordinates" | coordinates of mesh points |
| "Point" | points |
| "Arrow" | arrows |
| "PointLine" | points and lines |
| "LineSphere" | lines and spheres |
| "SphereTube" | spheres and tubes |
| "Sphere" | spheres |
| "Cuboid" | cuboids |
| "Cone" | cones |
| "Cylinder" | cylinders |
| "Line" | lines |
| "XTransversalLine" | lines in the x direction |
| "YTransversalLine" | lines in the y direction |
| "BezierCurve" | Bézier curves |
| "Polygon" | a mesh made with polygons |
| "TransversalPolygon" | polygons in the x and y direction |
| "XTransversalPolygon" | polygons in the x direction |
| "YTransversalPolygon" | polygons in the y direction |
| "Tube" | squares with circular hole |
| "XTransversalTube" | tubes in the x direction |
| "YTransversalTube" | tubes in the y direction |
| "Mesh" | squared mesh |
| "RandomColorMesh" | randomly colored mesh |
| "XTransversalStrip" | strips in the x direction |
| "YTransversalStrip" | strips in the y direction |
| "Holed" | delete alternating polygons |
| "Rhombus" | rhombuses |
| "RhombusHoled" | delete alternating rhombuses |
| "RandomPolygon" | randomly deleted polygons in the mesh |
| "DiskHoled" | squares with a circular hole |
| "Triangle" | squares subdivided into triangles |
| "XTransversalTriangle" | triangles in the x direction |
| "YTransversalTriangle" | triangles in the y direction |
| "ShrinkPolygon" | shrink polygons |
| "RotateScalePolygon" | rotate and scale polygons in the mesh |
| "PerturbedMesh" | randomly translate polygons |
| "PerturbedVertices" | randomly translate vertices |
| "Distorted" | translate vertices around an axis |
| "BSplineSurfaceOpen" | an open B–spline surface |
| "BSplineSurfaceClosed" | a closed B–spline surface |
| "ShortestTour" | shortest tour through the mesh points |
| "OutlinePolygons" | outlined polygons |
| "HexagonalMesh" | hexagonal mesh |
| "TriangulatedHexagonalMesh” | triangulated hexagonal mesh |
| "HexagonalMeshHoled" | triangulated hexagonal mesh with a deleted triangle |
| "OpacitySphereHexagonalMesh" | hexagonal mesh and spheres with opacity |
| "MeshRegion" | mesh regions |
| "DiscretizeRegion" | discretized polygons |
| "Points" | region of points |
| "SamplePoints" | sample points |
| "Lines" | region of lines |
| "Polygons" | region of polygons |
| "SphereAndTube" | region of spheres and tubes |
| "SmoothShading" | smooth shading region |
| "FaceNormals" | region with face normals |
| "CuboidRegion" | region with cuboids |
| "DelaunayMesh" | Delaunay mesh |
| "ConvexHullMesh" | convex hull mesh |
| texture | an image to be used as a texture |
| simple polyhedra | a simple polyhedra |
| custom polygon | an arbitrary polygon |
Parametric equations for a Klein bottle:
| In[1]:= |
|
| Out[1]= |
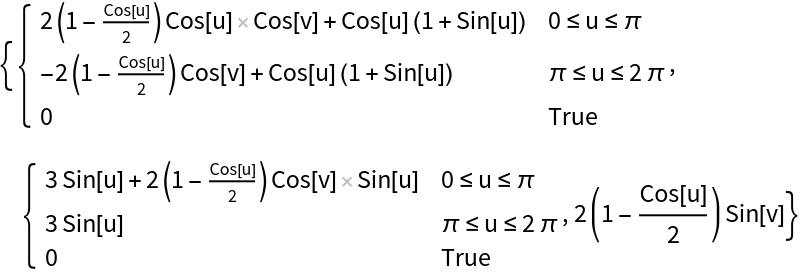
|
Get the coordinates of the mesh of the surface:
| In[2]:= |
|
| Out[2]= |

|
A surface plotted with ParametricPlot3D:
| In[3]:= |
![ParametricPlot3D[
Evaluate@Entity["Surface", "KleinBottle"][
EntityProperty["Surface", "ParametricEquations"]][1, 2, 3][u, v], {u, 0, 2 \[Pi]}, {v, 0, 2 \[Pi]}, Boxed -> False, Axes -> False]](https://www.wolframcloud.com/obj/resourcesystem/images/c88/c886ee98-474c-41ee-af3e-c29f6d8faae0/628a14b0e6d6d02e.png)
|
| Out[3]= |
|
Using points:
| In[4]:= |
![Graphics3D[
ResourceFunction["ApproximatedSurface"][
kb, {u, 0, 2 \[Pi], 35}, {v, 0, 2 \[Pi], 35}, "Point"], Boxed -> False, Axes -> False]](https://www.wolframcloud.com/obj/resourcesystem/images/c88/c886ee98-474c-41ee-af3e-c29f6d8faae0/77647e0d6f2b5862.png)
|
| Out[4]= |

|
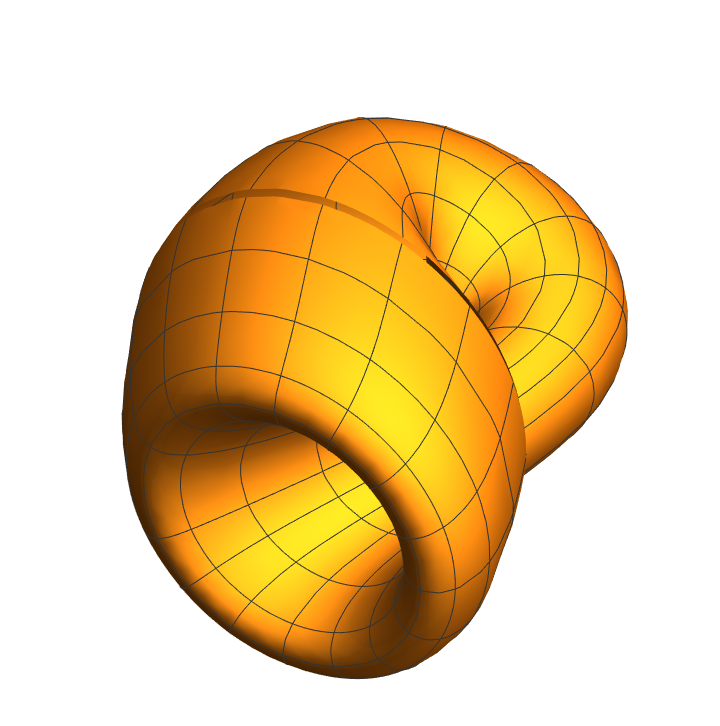
Using arrows:
| In[5]:= |
![Graphics3D[{Arrowheads[.015], ResourceFunction["ApproximatedSurface"][
kb, {u, 0, 2 \[Pi], 35}, {v, 0, 2 \[Pi], 35}, "Arrow"]}, Boxed -> False, Axes -> False]](https://www.wolframcloud.com/obj/resourcesystem/images/c88/c886ee98-474c-41ee-af3e-c29f6d8faae0/7b0a06f15872dd07.png)
|
| Out[5]= |
|
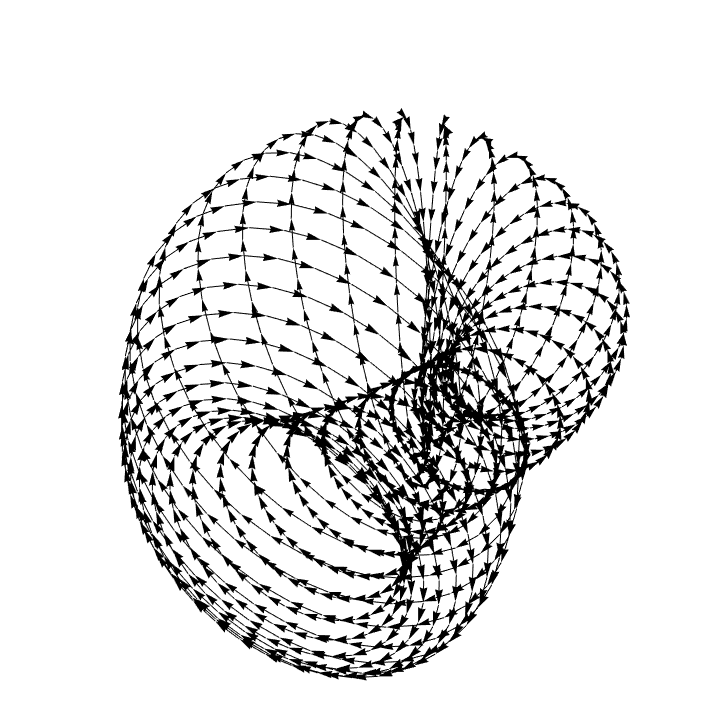
With lines and points:
| In[6]:= |
![Graphics3D[
ResourceFunction["ApproximatedSurface"][
kb, {u, 0, 2 \[Pi], 35}, {v, 0, 2 \[Pi], 35}, "PointLine"], Boxed -> False, Axes -> False]](https://www.wolframcloud.com/obj/resourcesystem/images/c88/c886ee98-474c-41ee-af3e-c29f6d8faae0/39c6cf73cd10f56b.png)
|
| Out[6]= |
|
With lines and spheres:
| In[7]:= |
![Graphics3D[
ResourceFunction["ApproximatedSurface"][
kb, {u, 0, 2 \[Pi], 35}, {v, 0, 2 \[Pi], 35}, "LineSphere"], Boxed -> False, Axes -> False]](https://www.wolframcloud.com/obj/resourcesystem/images/c88/c886ee98-474c-41ee-af3e-c29f6d8faae0/6e9d69d62834fdff.png)
|
| Out[7]= |

|
With spheres and tubes:
| In[8]:= |
![Graphics3D[
ResourceFunction["ApproximatedSurface"][
kb, {u, 0, 2 \[Pi], 35}, {v, 0, 2 \[Pi], 35}, {"SphereTube", .1, .05}], Boxed -> False, Axes -> False]](https://www.wolframcloud.com/obj/resourcesystem/images/c88/c886ee98-474c-41ee-af3e-c29f6d8faae0/3b60db57f7ed84d4.png)
|
| Out[8]= |

|
Using only spheres:
| In[9]:= |
![Graphics3D[
ResourceFunction["ApproximatedSurface"][
kb, {u, 0, 2 \[Pi], 35}, {v, 0, 2 \[Pi], 35}, "Sphere"], Boxed -> False, Axes -> False]](https://www.wolframcloud.com/obj/resourcesystem/images/c88/c886ee98-474c-41ee-af3e-c29f6d8faae0/7c901d4647027e4f.png)
|
| Out[9]= |

|
Modify the radius of the spheres:
| In[10]:= |
![Graphics3D[
ResourceFunction["ApproximatedSurface"][
kb, {u, 0, 2 \[Pi], 35}, {v, 0, 2 \[Pi], 35}, {"Sphere", .1}], Boxed -> False, Axes -> False]](https://www.wolframcloud.com/obj/resourcesystem/images/c88/c886ee98-474c-41ee-af3e-c29f6d8faae0/36459f57d739c016.png)
|
| Out[10]= |

|
Using cuboids:
| In[11]:= |
![Graphics3D[
ResourceFunction["ApproximatedSurface"][
kb, {u, 0, 2 \[Pi], 35}, {v, 0, 2 \[Pi], 35}, {"Cuboid", .2}], Boxed -> False, Axes -> False]](https://www.wolframcloud.com/obj/resourcesystem/images/c88/c886ee98-474c-41ee-af3e-c29f6d8faae0/5e504460a789aec9.png)
|
| Out[11]= |

|
Using other geometrical objects:
| In[12]:= |
![Graphics3D[
ResourceFunction["ApproximatedSurface"][
kb, {u, 0, 2 \[Pi], 35}, {v, 0, 2 \[Pi], 35}, {"Cone", .1, .2}], Boxed -> False, Axes -> False]](https://www.wolframcloud.com/obj/resourcesystem/images/c88/c886ee98-474c-41ee-af3e-c29f6d8faae0/700f8f8bec8af356.png)
|
| Out[12]= |

|
| In[13]:= |
![Graphics3D[
ResourceFunction["ApproximatedSurface"][
kb, {u, 0, 2 \[Pi], 35}, {v, 0, 2 \[Pi], 35}, {"Cylinder", .1, .2}],
Boxed -> False, Axes -> False]](https://www.wolframcloud.com/obj/resourcesystem/images/c88/c886ee98-474c-41ee-af3e-c29f6d8faae0/33182f0707c48cb6.png)
|
| Out[13]= |

|
| In[14]:= |
![Graphics3D[
ResourceFunction["ApproximatedSurface"][
kb, {u, 0, 2 \[Pi], 35}, {v, 0, 2 \[Pi], 35}, Dodecahedron[]], Boxed -> False, Axes -> False]](https://www.wolframcloud.com/obj/resourcesystem/images/c88/c886ee98-474c-41ee-af3e-c29f6d8faae0/6efd42f97686c1b6.png)
|
| Out[14]= |

|
Using lines:
| In[15]:= |
![GraphicsRow[
Graphics3D[
ResourceFunction["ApproximatedSurface"][
kb, {u, 0, 2 \[Pi], 35}, {v, 0, 2 \[Pi], 35}, #], Boxed -> False,
Axes -> False] & /@ {"XTransversalLine", "YTransversalLine", "Line"}]](https://www.wolframcloud.com/obj/resourcesystem/images/c88/c886ee98-474c-41ee-af3e-c29f6d8faae0/0ee9c9f490827ad4.png)
|
| Out[15]= |
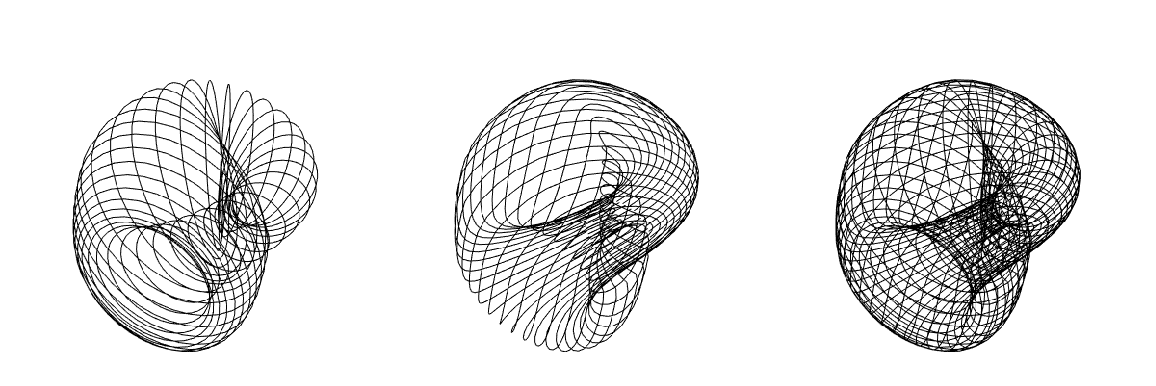
|
Using BezierCurve:
| In[16]:= |
![Graphics3D[
ResourceFunction["ApproximatedSurface"][
kb, {u, 0, 2 \[Pi], 35}, {v, 0, 2 \[Pi], 35}, "BezierCurve"], Boxed -> False, Axes -> False]](https://www.wolframcloud.com/obj/resourcesystem/images/c88/c886ee98-474c-41ee-af3e-c29f6d8faae0/6a236b8a69e7a394.png)
|
| Out[16]= |
|
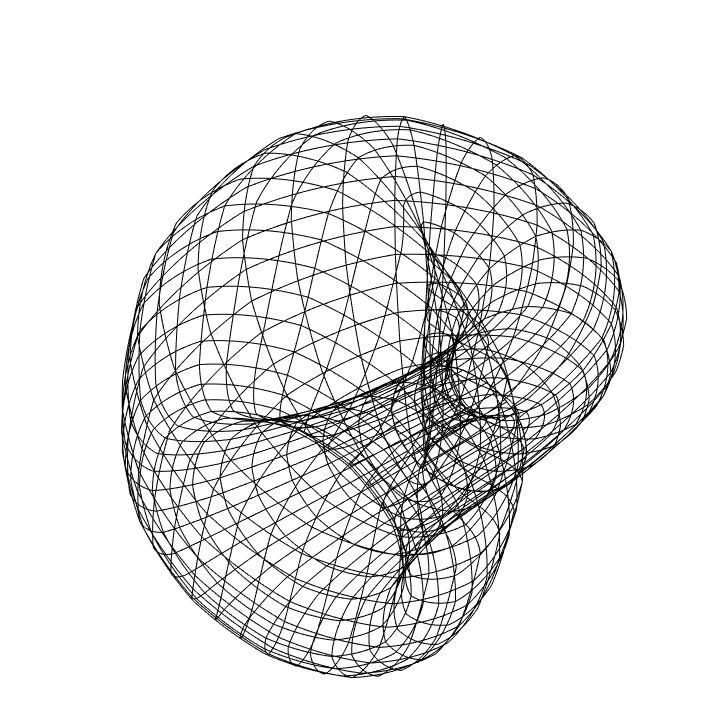
Using transversal polygons:
| In[17]:= |
![GraphicsRow[
Graphics3D[
ResourceFunction["ApproximatedSurface"][
kb, {u, 0, 2 \[Pi], 35}, {v, 0, 2 \[Pi], 35}, #], Boxed -> False,
Axes -> False] & /@ {"XTransversalPolygon", "YTransversalPolygon"}]](https://www.wolframcloud.com/obj/resourcesystem/images/c88/c886ee98-474c-41ee-af3e-c29f6d8faae0/1dd3f91a1cef621d.png)
|
| Out[17]= |

|
| In[18]:= |
![Graphics3D[
ResourceFunction["ApproximatedSurface"][
kb, {u, 0, 2 \[Pi], 35}, {v, 0, 2 \[Pi], 35}, "TransversalPolygon"],
Boxed -> False, Axes -> False]](https://www.wolframcloud.com/obj/resourcesystem/images/c88/c886ee98-474c-41ee-af3e-c29f6d8faae0/40658147b815826f.png)
|
| Out[18]= |
|
Using tubes:
| In[19]:= |
![GraphicsRow[
Graphics3D[
ResourceFunction["ApproximatedSurface"][
kb, {u, 0, 2 \[Pi], 35}, {v, 0, 2 \[Pi], 35}, #], Boxed -> False,
Axes -> False] & /@ {"XTransversalTube", "YTransversalTube", "Tube"}]](https://www.wolframcloud.com/obj/resourcesystem/images/c88/c886ee98-474c-41ee-af3e-c29f6d8faae0/661806155e7fdb11.png)
|
| Out[19]= |

|
Using polygons:
| In[20]:= |
![Graphics3D[
ResourceFunction["ApproximatedSurface"][
kb, {u, 0, 2 \[Pi], 70}, {v, 0, 2 \[Pi], 70}, "Mesh"], Boxed -> False, Axes -> False]](https://www.wolframcloud.com/obj/resourcesystem/images/c88/c886ee98-474c-41ee-af3e-c29f6d8faae0/79c0fe4383c11abf.png)
|
| Out[20]= |
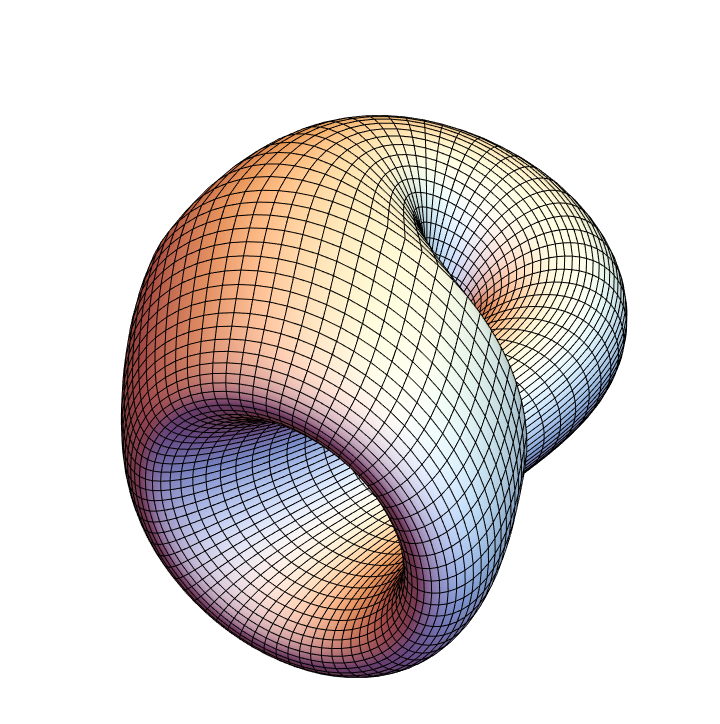
|
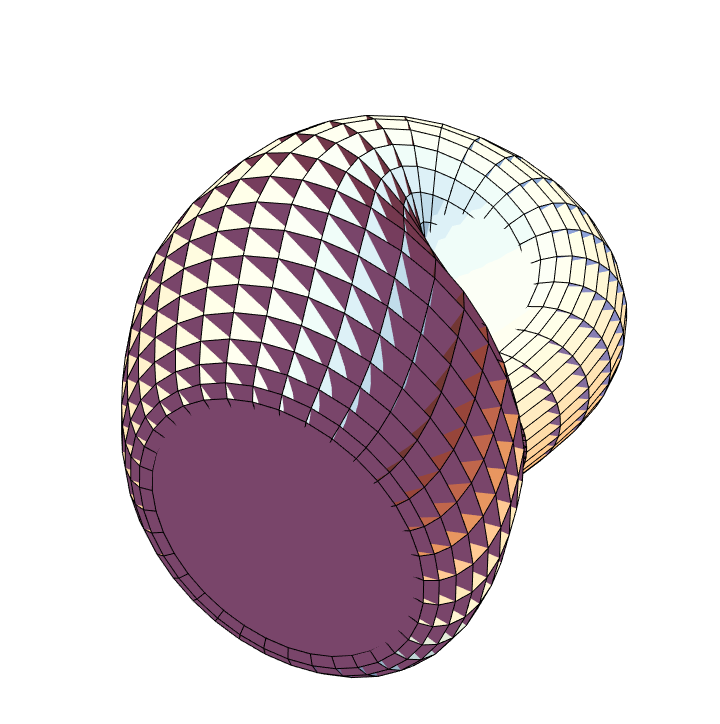
With a texture:
| In[21]:= |
![Graphics3D[{EdgeForm[], ResourceFunction["ApproximatedSurface"][
kb, {u, 0, 2 \[Pi], 35}, {v, 0, 2 \[Pi], 35}, \!\(\*
GraphicsBox[
TagBox[RasterBox[CompressedData["
1:eJzt1bGrl1Ucx/GDZYUEEgghhCFCGEFElyCi+3tKCCOE0AIJJLiFEihlilRG
4OLScpcWG1p0aHJpuUuLDi02NLm03KXFhpbb0NQV+jzP+Z4/IV4HEt8pt+9z
vpxehz/67NS5Pa21y0/s/nJq44s3L13a+Oq9xx7G2Y0Lay9feGT3t2f/++fR
9vBcm1o5S++7f+T12jdLb97ZGf78yHrfv947sV7//pXSz5/ZXB9+fuk/T24N
P+9e6dvHt4efv1N669DeVf3v7S/9/Y2Dq2H+0l8feHFV53m19JnNY6vhe0uv
7zu9qvNulH72+vnVcD+ruo9rq/o910t/vv7t8H2bpbevfjd8743Sp7Z+GL7/
Zum7Oz8O93G79NraT8P9bJW+dfHn4b7ulD5w+5fh/u6Vvv7gt+E+75f+++jv
w/1ulz537o/hvh+Uvn/zr+H+d0q/vf3PsI821e/ZM9X97J3q9z0+1X3tm+r3
PjnV/e2f6vc/NdV9HpjqfTw91f0enOr9PDPVfR+a6n0dnur+j0z1/p4rfXfn
6FTv84XSu+9lqvf7Uum1tbWp3vcrpXff11Tv/7XSty6uT3Ufbwz7ODbs461h
H8eHfbwz7OPEsI93h32cHPbx/rCP08M+Phj2cWbYx4fDPjaGfXw87OPcsI9P
hn2cH/bx6bCPi8M+Lg/7uDLs48thH1eHfXwz7OPa0Pl3+R6e8IQnbTnD/794
whOetPnwhCc8SfOEJzzhSTcPT3jSvT+e8IQnaZ7whCc8SfOEJzzhyTIvT3jC
kzRPeMITnqR5whOe8KTNhyc84UmaJzzhCU+6eXjCk+798YQnPEnzhCc84Uma
JzzhCU+WeXnCE56kecITnvAkzROe8IQnbT484QlP0jzhCU940s3DE550748n
POFJmic84QlP0jzhCU94sszLE57wJM0TnvCEJ2me8IQnPGnz4QlPeJLmCU94
wpNuHp7wpHt/POEJT9I84QlPeJLmCU94wpNlXp7whCdpnvCEJzxJ84QnPOFJ
mw9PeMKTNE94whOedPPwhCfd++MJT3iS5glPeMKTNE94whOeLPPyhCc8SfOE
JzzhSZonPOEJT9p8eMITnqR5whOe8KSbhyc86d4fT3jCkzRPeMITnqR5whOe
8GSZlyc84UmaJzzhCU/SPOEJT3jS5sMTnvAkzROe8IQn3Tw84Un3/njCE56k
ecITnvAkzROe8IQny7w84QlP0jzhCU94kuYJT3jCkzYfnvCEJ2me8IQnPOnm
4QlPuvfHE57wJM0TnvCEJ2me8IQnPFnm5QlPeJLmCU94wpM0T3jCE560+fCE
JzxJ84QnPOFJNw9PeNK9P57whCdpnvCEJzxJ84QnPOHJMi9PeMKTNE94whOe
pHnCE57wpM2HJzzhSZonPOEJT7p5eMKT7v3xhCc8SfOEJzzhSZonPOEJT5Z5
ecITnqR5whOe8CTNE57whCdtPjzhCU/SPOEJT3jSzcMTnnTvjyc84UmaJzzh
CU/SPOEJT3iyzMsTnvAkzROe8IQnaZ7whCc8afPhCU94kuYJT3jCk24envCk
e3884QlP0jzhCU94kuYJT3jCk2VenvCEJ2me8IQnPEnzhCc84UmbD094wpM0
T3jCE5508/CEJ9374wlPeJLmCU94wpM0T3jCE54s8/KEJzxJ84QnPOFJmic8
4QlP2nx4whOepHnCE57wpJuHJzzp3h9PeMKTNE94whOepHnCE57wZJmXJzzh
SZonPOEJT9I84QlPeNLmwxOe8CTNE57whCfdPDzhSff+eMITnqR5whOe8CTN
E57whCfLvDzhCU/SPOEJT3iS5glPeMKTNh+e8IQnaZ7whCc86ebhCU+698cT
nvAkzROe8IQnaZ7whCc8WeblCU94kuYJT3jCkzRPeMITnrT58IQnPEnzhCc8
4Uk3D0940r0/nvCEJ2me8IQnPEnzhCc84ckyL094wpM0T3jCE56kecITnvCk
zYcnPOFJmic84QlPunl4wpPu/fGEJzxJ84QnPOFJmic84QlPlnl5whOepHnC
E57wJM0TnvCEJ20+POEJT9I84QlPeNLNwxOedO+PJzzhSZonPOEJT9I84QlP
eLLMyxOe8CTNE57whCdpnvCEJzxp8+EJT3iS5glPeMKTbh6e8KR7fzzhCU/S
POEJT3iS5glPeMKTZV6e8IQnaZ78/zz5F/JBkaE=
"], {{0, 101.}, {101., 0}}, {
0., 1.},
ColorFunction->RGBColor],
BoxForm`ImageTag["Real32", ColorSpace -> "RGB", Interleaving -> True],
Selectable->False],
DefaultBaseStyle->"ImageGraphics",
ImageSizeRaw->{101., 101.},
PlotRange->{{0, 101.}, {0, 101.}}]\)]}, Boxed -> False, Axes -> False]](https://www.wolframcloud.com/obj/resourcesystem/images/c88/c886ee98-474c-41ee-af3e-c29f6d8faae0/24a17a5f74b8baaa.png)
|
| Out[21]= |

|
A randomly colored mesh:
| In[22]:= |
![Graphics3D[
ResourceFunction["ApproximatedSurface"][
kb, {u, 0, 2 \[Pi], 70}, {v, 0, 2 \[Pi], 70}, "RandomColorMesh"], Boxed -> False, Axes -> False, Lighting -> "Neutral"]](https://www.wolframcloud.com/obj/resourcesystem/images/c88/c886ee98-474c-41ee-af3e-c29f6d8faae0/3f52b8b15983e7af.png)
|
| Out[22]= |

|
With strips:
| In[23]:= |
![Graphics3D[
ResourceFunction["ApproximatedSurface"][
kb, {u, 0, 2 \[Pi], 34}, {v, 0, 2 \[Pi], 35}, "XTransversalStrip"], Boxed -> False, Axes -> False]](https://www.wolframcloud.com/obj/resourcesystem/images/c88/c886ee98-474c-41ee-af3e-c29f6d8faae0/4aeb419cb325e9d7.png)
|
| Out[23]= |

|
With holes:
| In[24]:= |
![Graphics3D[
ResourceFunction["ApproximatedSurface"][
kb, {u, 0, 2 \[Pi], 35}, {v, 0, 2 \[Pi], 35}, "Holed"], Boxed -> False, Axes -> False]](https://www.wolframcloud.com/obj/resourcesystem/images/c88/c886ee98-474c-41ee-af3e-c29f6d8faae0/48cc5be9782ce650.png)
|
| Out[24]= |
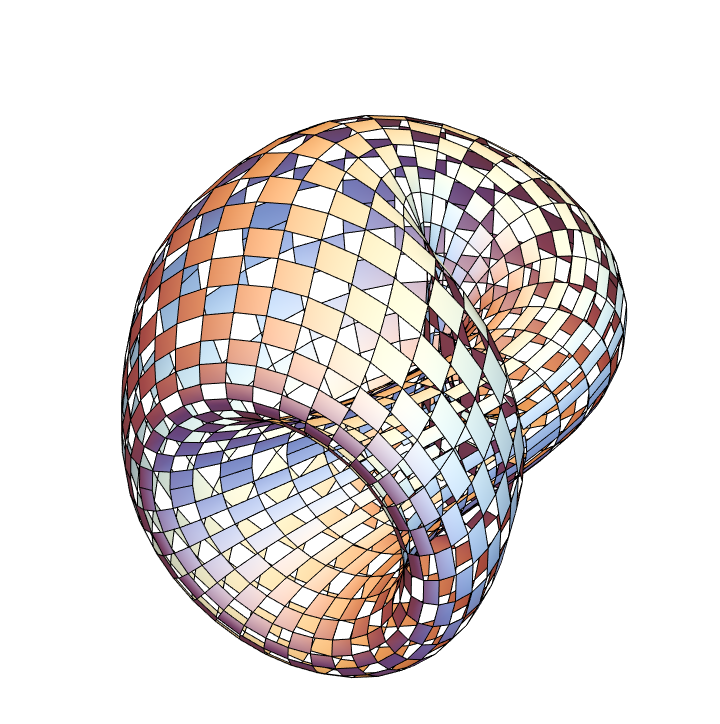
|
Using rhombuses:
| In[25]:= |
![Graphics3D[
ResourceFunction["ApproximatedSurface"][
kb, {u, 0, 2 \[Pi], 35}, {v, 0, 2 \[Pi], 34}, "Rhombus"], Boxed -> False, Axes -> False]](https://www.wolframcloud.com/obj/resourcesystem/images/c88/c886ee98-474c-41ee-af3e-c29f6d8faae0/4a117226721812e7.png)
|
| Out[25]= |
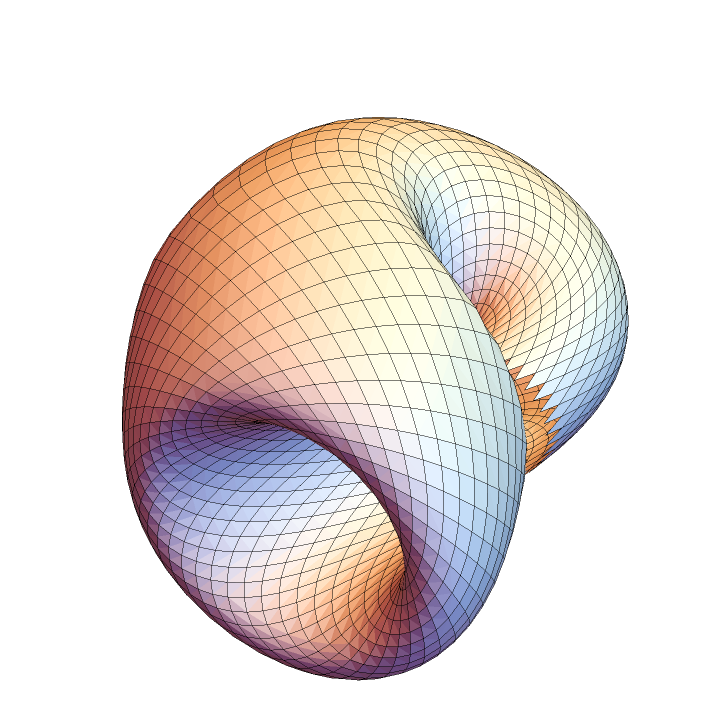
|
| In[26]:= |
![Graphics3D[
ResourceFunction["ApproximatedSurface"][
kb, {u, 0, 2 \[Pi], 35}, {v, 0, 2 \[Pi], 34}, "RhombusHoled"], Boxed -> False, Axes -> False, PlotRange -> All]](https://www.wolframcloud.com/obj/resourcesystem/images/c88/c886ee98-474c-41ee-af3e-c29f6d8faae0/72d2164f34030aad.png)
|
| Out[26]= |
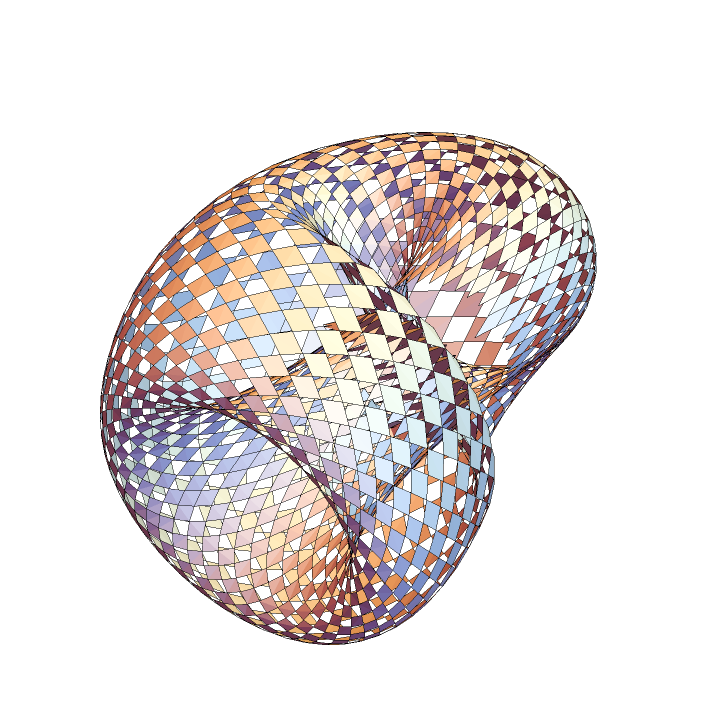
|
Randomly remove polygons:
| In[27]:= |
![Graphics3D[
ResourceFunction["ApproximatedSurface"][
kb, {u, 0, 2 \[Pi], 35}, {v, 0, 2 \[Pi], 35}, "RandomPolygon"], Boxed -> False, Axes -> False]](https://www.wolframcloud.com/obj/resourcesystem/images/c88/c886ee98-474c-41ee-af3e-c29f6d8faae0/2b048f896052a08e.png)
|
| Out[27]= |

|
Use transparency in a texture to put in holes:
| In[28]:= |
![Graphics3D[
ResourceFunction["ApproximatedSurface"][
kb, {u, 0, 2 \[Pi], 70}, {v, 0, 2 \[Pi], 70}, "DiskHoled"], Boxed -> False, Axes -> False]](https://www.wolframcloud.com/obj/resourcesystem/images/c88/c886ee98-474c-41ee-af3e-c29f6d8faae0/4813b91e738b89bb.png)
|
| Out[28]= |

|
Using triangles:
| In[29]:= |
![Graphics3D[
ResourceFunction["ApproximatedSurface"][
kb, {u, 0, 2 \[Pi], 40}, {v, 0, 2 \[Pi], 70}, "XTransversalTriangle"], Boxed -> False, Axes -> False]](https://www.wolframcloud.com/obj/resourcesystem/images/c88/c886ee98-474c-41ee-af3e-c29f6d8faae0/51e0a500435f97c4.png)
|
| Out[29]= |

|
| In[30]:= |
![Graphics3D[
ResourceFunction["ApproximatedSurface"][
kb, {u, 0, 2 \[Pi], 25}, {v, 0, 2 \[Pi], 25}, "Triangle"], Boxed -> False, Axes -> False]](https://www.wolframcloud.com/obj/resourcesystem/images/c88/c886ee98-474c-41ee-af3e-c29f6d8faae0/3c569cb99b552b0a.png)
|
| Out[30]= |
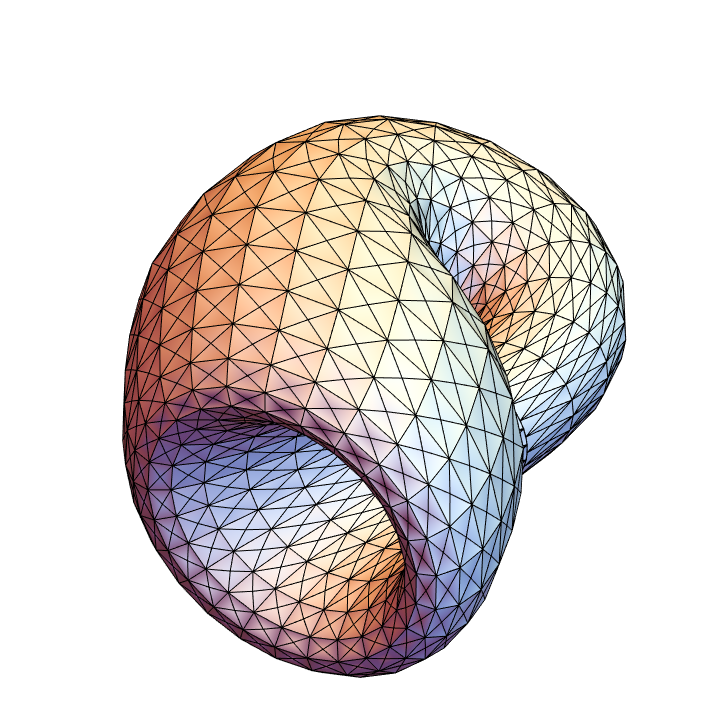
|
Shrink the polygons:
| In[31]:= |
![Graphics3D[
ResourceFunction["ApproximatedSurface"][
kb, {u, 0, 2 \[Pi], 35}, {v, 0, 2 \[Pi], 35}, "ShrinkPolygon"], Boxed -> False, Axes -> False]](https://www.wolframcloud.com/obj/resourcesystem/images/c88/c886ee98-474c-41ee-af3e-c29f6d8faae0/072326a0b3e72bfc.png)
|
| Out[31]= |

|
Rotate and scale the polygons:
| In[32]:= |
![Graphics3D[
ResourceFunction["ApproximatedSurface"][
kb, {u, 0, 2 \[Pi], 25}, {v, 0, 2 \[Pi], 25}, {"RotateScalePolygon", \[Pi]/6., .7}], Boxed -> False, Axes -> False]](https://www.wolframcloud.com/obj/resourcesystem/images/c88/c886ee98-474c-41ee-af3e-c29f6d8faae0/572e25971f575a3f.png)
|
| Out[32]= |

|
Randomly translate polygons:
| In[33]:= |
![Graphics3D[
ResourceFunction["ApproximatedSurface"][
kb, {u, 0, 2 \[Pi], 70}, {v, 0, 2 \[Pi], 70}, "PerturbedMesh"], Boxed -> False, Axes -> False]](https://www.wolframcloud.com/obj/resourcesystem/images/c88/c886ee98-474c-41ee-af3e-c29f6d8faae0/3e25ccd6fbe19b7e.png)
|
| Out[33]= |

|
Randomly translate vertices:
| In[34]:= |
![Graphics3D[{EdgeForm[], ResourceFunction["ApproximatedSurface"][
kb, {u, 0, 2 \[Pi], 35}, {v, 0, 2 \[Pi], 35}, {"PerturbedVertices", .1}]}, Boxed -> False, Axes -> False]](https://www.wolframcloud.com/obj/resourcesystem/images/c88/c886ee98-474c-41ee-af3e-c29f6d8faae0/48478c2bd14a0897.png)
|
| Out[34]= |
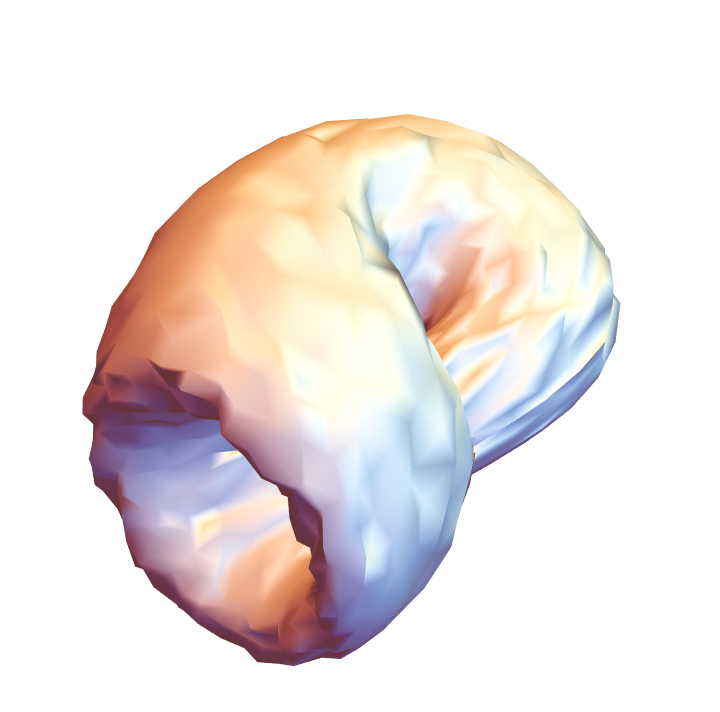
|
Distort polygons around an axis of rotation with a varying parameter:
| In[35]:= |
![Graphics3D[
ResourceFunction["ApproximatedSurface"][
kb, {u, 0, 2 \[Pi], 70}, {v, 0, 2 \[Pi], 70}, {"Distorted", 4/11, {0, 0, 1}}], Boxed -> False, Axes -> False]](https://www.wolframcloud.com/obj/resourcesystem/images/c88/c886ee98-474c-41ee-af3e-c29f6d8faae0/20722c620daaecc0.png)
|
| Out[35]= |
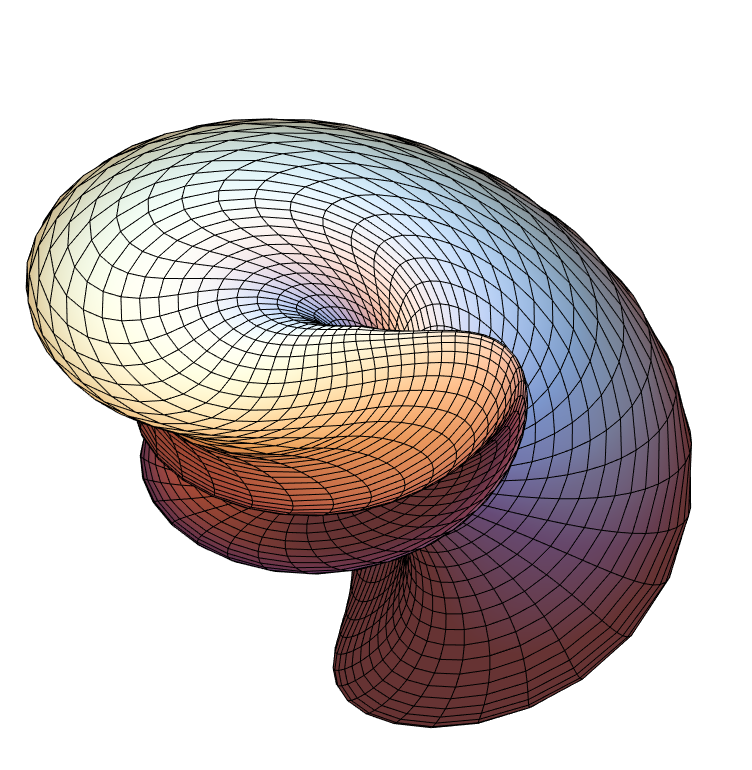
|
Use a BSplineSurface:
| In[36]:= |
![Graphics3D[
ResourceFunction["ApproximatedSurface"][
kb, {u, 0, 2 \[Pi], 15}, {v, 0, 2 \[Pi], 15}, "BSplineSurfaceClosed"], Boxed -> False, Axes -> False]](https://www.wolframcloud.com/obj/resourcesystem/images/c88/c886ee98-474c-41ee-af3e-c29f6d8faae0/1e4a15beaaa3654c.png)
|
| Out[36]= |
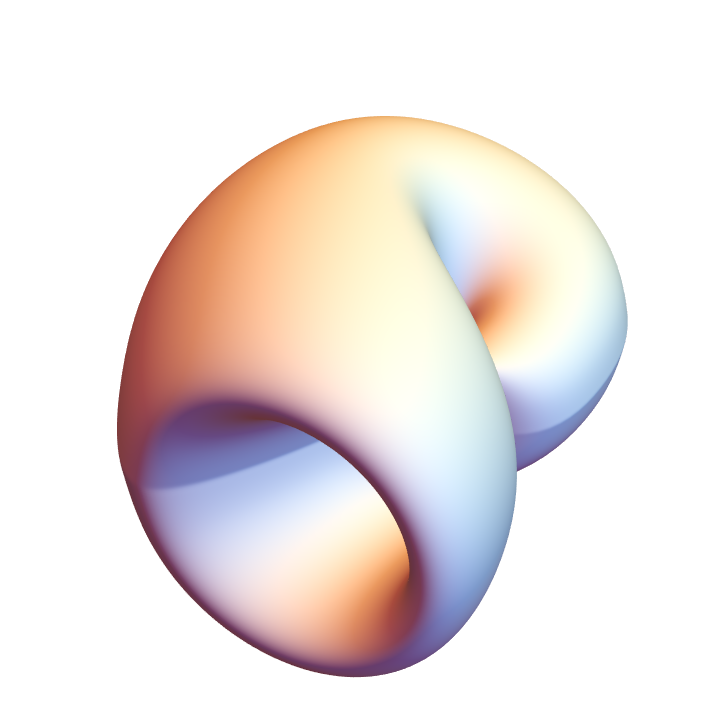
|
Shortest tour through the mesh:
| In[37]:= |
![Graphics3D[
ResourceFunction["ApproximatedSurface"][
kb, {u, 0, 2 \[Pi], 70}, {v, 0, 2 \[Pi], 70}, "ShortestTour"], Boxed -> False, Axes -> False]](https://www.wolframcloud.com/obj/resourcesystem/images/c88/c886ee98-474c-41ee-af3e-c29f6d8faae0/47c5429fa8d42662.png)
|
| Out[37]= |

|
For a surface with edges:
| In[38]:= |
|
| Out[38]= |
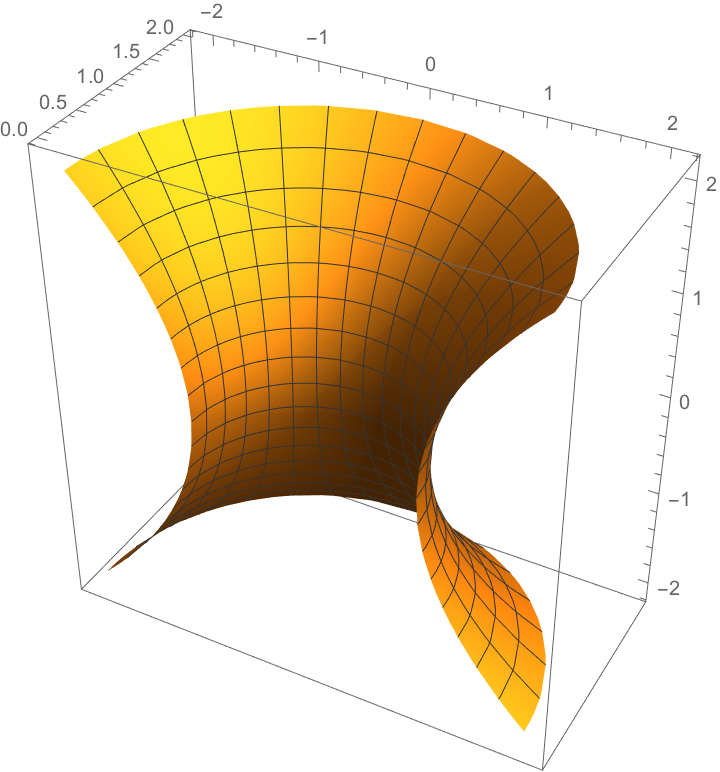
|
An open B-spline:
| In[39]:= |
![Graphics3D[{Opacity[.5], ResourceFunction[
"ApproximatedSurface"][{(1 + v^2) Cos[u], (1 + v^2) Sin[u], 2 v}, {u, 0, \[Pi], 15}, {v, -1, 1, 15}, "BSplineSurfaceOpen"]}, Boxed -> False, Axes -> False]](https://www.wolframcloud.com/obj/resourcesystem/images/c88/c886ee98-474c-41ee-af3e-c29f6d8faae0/3dfc7adf808935d8.png)
|
| Out[39]= |
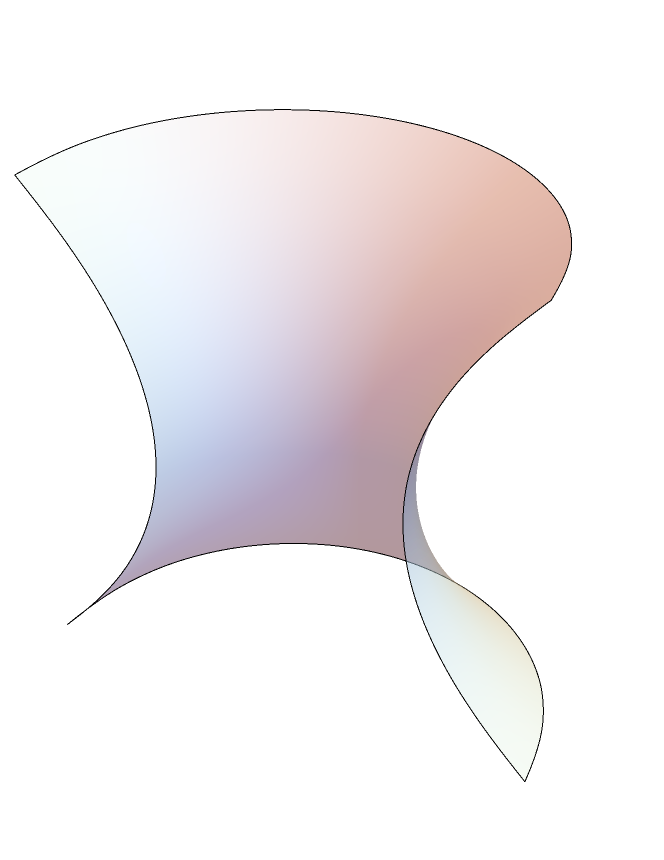
|
A closed B-spline:
| In[40]:= |
![Graphics3D[{Opacity[.5], ResourceFunction[
"ApproximatedSurface"][{(1 + v^2) Cos[u], (1 + v^2) Sin[u], 2 v}, {u, 0, \[Pi], 15}, {v, -1, 1, 15}, "BSplineSurfaceClosed"]},
Boxed -> False, Axes -> False]](https://www.wolframcloud.com/obj/resourcesystem/images/c88/c886ee98-474c-41ee-af3e-c29f6d8faae0/060c38b4391f70a4.png)
|
| Out[40]= |

|
Parametric equations for a Klein bottle:
| In[41]:= |
|
| Out[41]= |
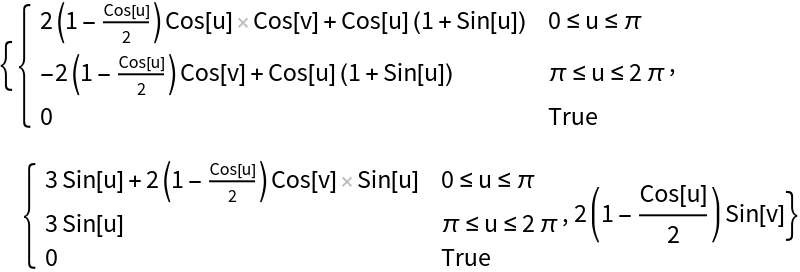
|
With a perforated polygon:
| In[42]:= |
![Graphics3D[{EdgeForm[], ResourceFunction["ApproximatedSurface"][
kb, {u, 0, 2 \[Pi], 35}, {v, 0, 2 \[Pi], 35}, Polygon[{{0., 0., 0.}, {0., 1., 0.}, {0.2, 0.2, 0.}, {0.2, 0.8, 0.}, {0.8, 0.2, 0.}, {0.8, 0.8, 0.}, {1., 0., 0.}, {1., 1., 0.}}, {1, 7, 8, 2} -> {{4, 6, 5, 3}}]]}, Boxed -> False]](https://www.wolframcloud.com/obj/resourcesystem/images/c88/c886ee98-474c-41ee-af3e-c29f6d8faae0/50502a7616c61978.png)
|
| Out[42]= |

|
With outlined polygons:
| In[43]:= |
![Graphics3D[
ResourceFunction["ApproximatedSurface"][
kb, {u, 0, 2 \[Pi], 35}, {v, 0, 2 \[Pi], 35}, "OutlinePolygons"], Boxed -> False, Axes -> False]](https://www.wolframcloud.com/obj/resourcesystem/images/c88/c886ee98-474c-41ee-af3e-c29f6d8faae0/09620d9aa8f5fc8e.png)
|
| Out[43]= |

|
With disks:
| In[44]:= |
![Graphics3D[
ResourceFunction["ApproximatedSurface"][
kb, {u, 0, 2 \[Pi], 35}, {v, 0, 2 \[Pi], 35}, Polygon[{{0.5, 0., 0}, {0.47552825814757677`, 0.15450849718747373`, 0}, {0.4045084971874737, 0.29389262614623657`, 0}, {0.29389262614623657`, 0.4045084971874737, 0}, {0.15450849718747373`, 0.47552825814757677`, 0}, {0., 0.5, 0}, {-0.15450849718747373`, 0.47552825814757677`, 0}, {-0.29389262614623657`, 0.4045084971874737, 0}, {-0.4045084971874737, 0.29389262614623657`, 0}, {-0.47552825814757677`, 0.15450849718747373`, 0}, {-0.5, 0., 0}, {-0.47552825814757677`, -0.15450849718747373`, 0}, {-0.4045084971874737, -0.29389262614623657`, 0}, {-0.29389262614623657`, -0.4045084971874737, 0}, {-0.15450849718747373`, -0.47552825814757677`, 0}, {0., -0.5,
0}, {0.15450849718747373`, -0.47552825814757677`, 0}, {0.29389262614623657`, -0.4045084971874737, 0}, {0.4045084971874737, -0.29389262614623657`, 0}, {0.47552825814757677`, -0.15450849718747373`, 0}, {0.5, 0., 0}}]], Boxed -> False]](https://www.wolframcloud.com/obj/resourcesystem/images/c88/c886ee98-474c-41ee-af3e-c29f6d8faae0/71099688f32629bd.png)
|
| Out[44]= |

|
With a 3D disk using BSplineSurface:
| In[45]:= |
![Graphics3D[
ResourceFunction["ApproximatedSurface"][
kb, {u, 0, 2 \[Pi], 35}, {v, 0, 2 \[Pi], 35}, BSplineSurface[.35 {{{1, 0, 0}, {1, 1, 0}, {0, 1, 0}}, {{1, -1, 0}, {0, 0, 0}, {-1, 1, 0}}, {{0, -1, 0}, {-1, -1, 0}, {-1, 0, 0}}}, SplineKnots -> {{0, 0, 0, 1, 1, 2}, {0, 0, 0, 1, 1, 2}}, SplineWeights -> {{1, 1/Sqrt[2], 1}, {1/Sqrt[2], 1, 1/Sqrt[2]}, {1,
1/Sqrt[2], 1}}]], PlotRange -> {{-4.1, 2.5}, {-3., 5.1}, {-3., 3.}}]](https://www.wolframcloud.com/obj/resourcesystem/images/c88/c886ee98-474c-41ee-af3e-c29f6d8faae0/55fc81a40b6e34cd.png)
|
| Out[45]= |

|
A hexagonal mesh:
| In[46]:= |
![Graphics3D[
ResourceFunction["ApproximatedSurface"][
kb, {u, 0, 2 \[Pi], 30}, {v, 0, 2 \[Pi], 29}, "HexagonalMesh"], Boxed -> False, Axes -> False]](https://www.wolframcloud.com/obj/resourcesystem/images/c88/c886ee98-474c-41ee-af3e-c29f6d8faae0/684d09dc7758b01c.png)
|
| Out[46]= |
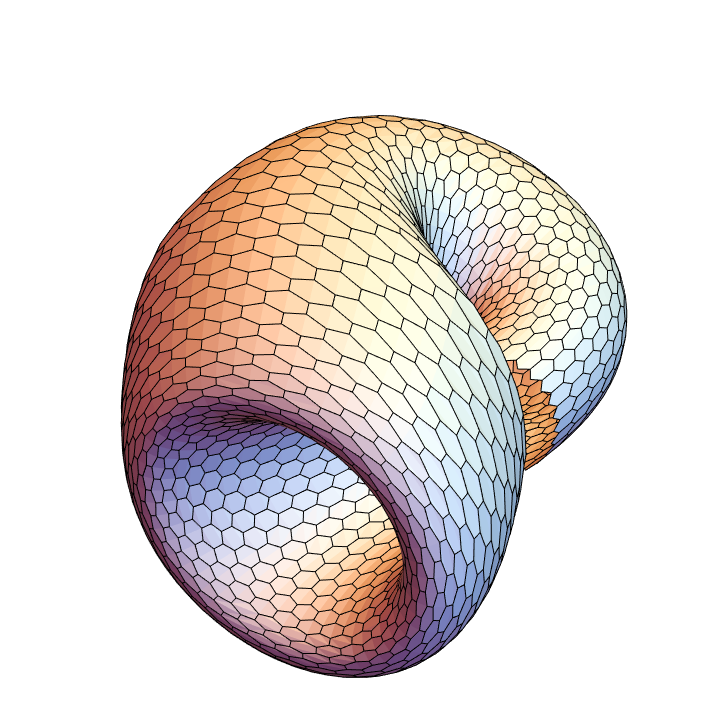
|
A hexagonal mesh subdivided with triangles:
| In[47]:= |
![Graphics3D[
ResourceFunction["ApproximatedSurface"][
kb, {u, 0, 2 \[Pi], 16}, {v, 0, 2 \[Pi], 15}, "TriangulatedHexagonalMesh"], Boxed -> False, Axes -> False]](https://www.wolframcloud.com/obj/resourcesystem/images/c88/c886ee98-474c-41ee-af3e-c29f6d8faae0/7f43c1821a504208.png)
|
| Out[47]= |
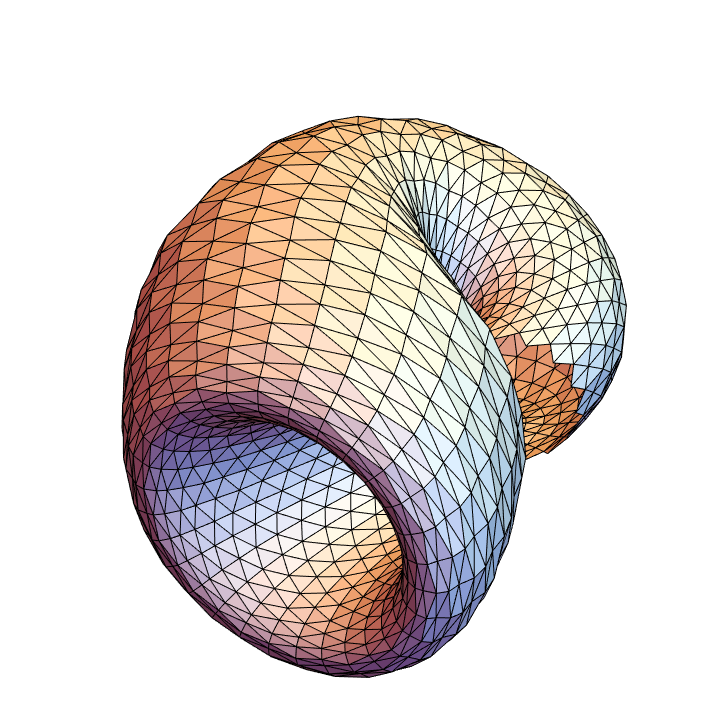
|
A hexagonal mesh with holes:
| In[48]:= |
![Graphics3D[
ResourceFunction["ApproximatedSurface"][
kb, {u, 0, 2 \[Pi], 14}, {v, 0, 2 \[Pi], 13}, "HexagonalMeshHoled"],
Boxed -> False]](https://www.wolframcloud.com/obj/resourcesystem/images/c88/c886ee98-474c-41ee-af3e-c29f6d8faae0/20ea752dd3f9ef1d.png)
|
| Out[48]= |

|
A translucent hexagonal mesh with spheres:
| In[49]:= |
![Graphics3D[
ResourceFunction["ApproximatedSurface"][
kb, {u, 0, 2 \[Pi], 20}, {v, 0, 2 \[Pi], 20}, "OpacitySphereHexagonalMesh"], Boxed -> False]](https://www.wolframcloud.com/obj/resourcesystem/images/c88/c886ee98-474c-41ee-af3e-c29f6d8faae0/52a50f359024be90.png)
|
| Out[49]= |

|
Use discretized slices:
| In[50]:= |
![Graphics3D[
ResourceFunction["ApproximatedSurface"][
kb, {u, 0, 2 \[Pi], 14}, {v, 0, 2 \[Pi], 13}, "DiscretizeRegion"], Boxed -> False]](https://www.wolframcloud.com/obj/resourcesystem/images/c88/c886ee98-474c-41ee-af3e-c29f6d8faae0/79574f91e9e87e12.png)
|
| Out[50]= |
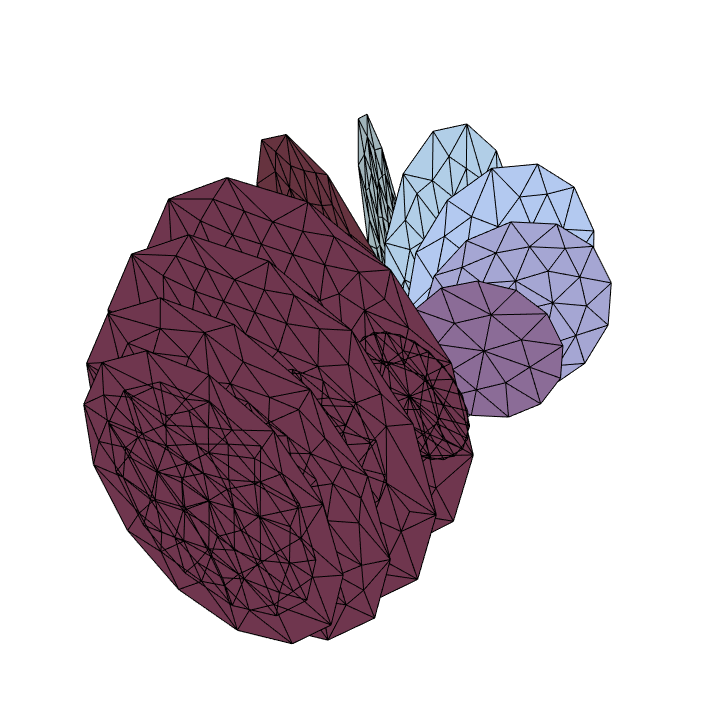
|
Using regions, with the plot themes available for regions:
| In[51]:= |
|
| Out[51]= |
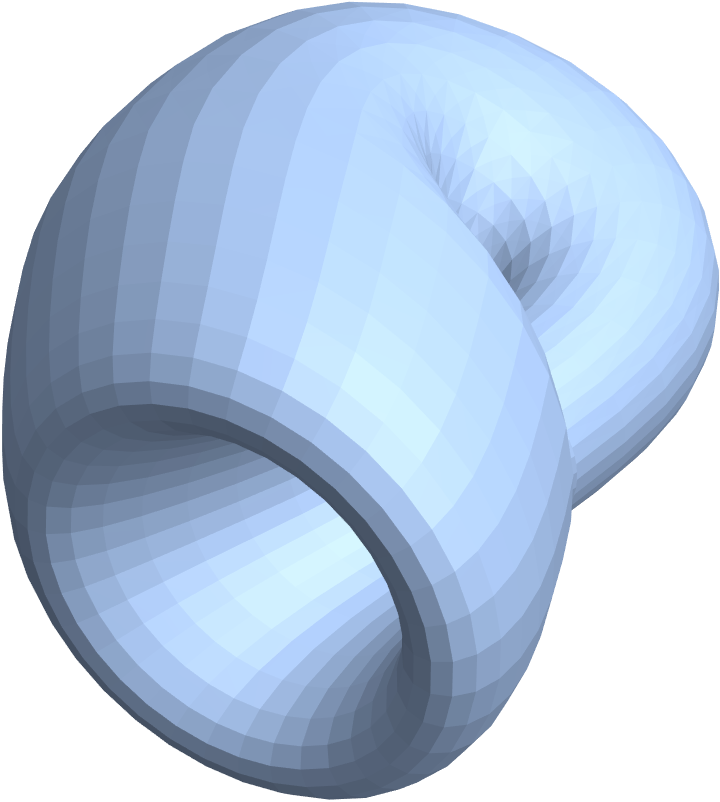
|
| In[52]:= |
![GraphicsRow[
ResourceFunction["ApproximatedSurface"][
kb, {u, 0, 2 \[Pi], 35}, {v, 0, 2 \[Pi], 35}, #] & /@ {"Points", "SamplePoints"}]](https://www.wolframcloud.com/obj/resourcesystem/images/c88/c886ee98-474c-41ee-af3e-c29f6d8faae0/59258d070d2634a4.png)
|
| Out[52]= |

|
| In[53]:= |
|
| Out[53]= |
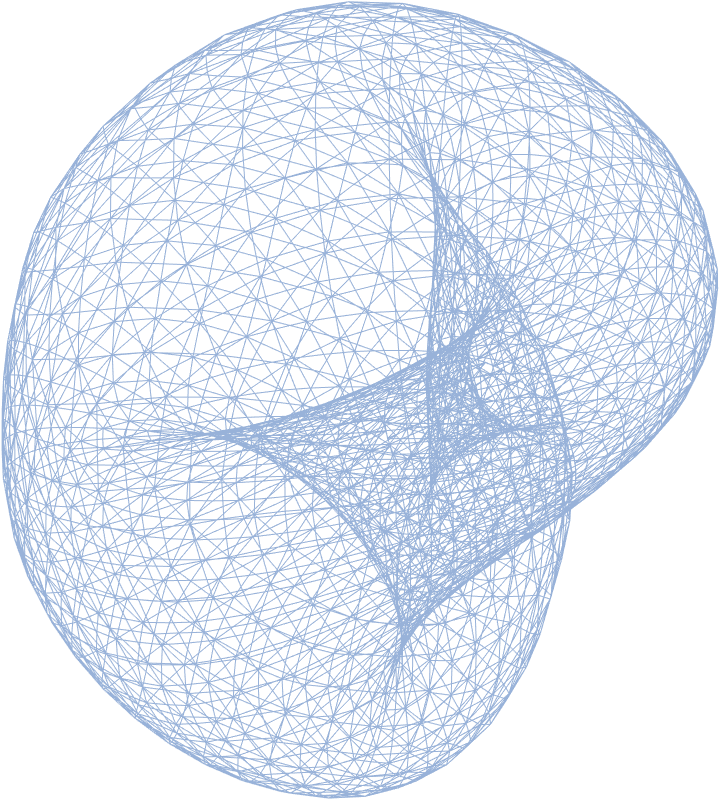
|
| In[54]:= |
|
| Out[54]= |
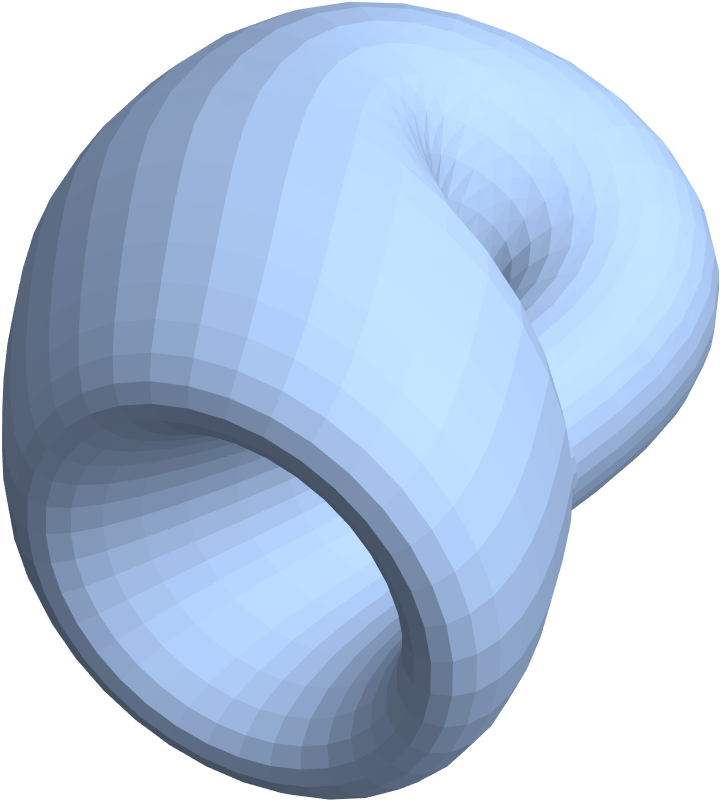
|
| In[55]:= |
|
| Out[55]= |

|
| In[56]:= |
|
| Out[56]= |

|
| In[57]:= |
|

Here the cuboids are converted into pyramids to be a region:
| In[58]:= |
|
| Out[58]= |

|
This work is licensed under a Creative Commons Attribution 4.0 International License