Scope (5)
Use the greedy heuristic to find an approximate vertex cover starting from the full vertex set:
This is the same as:
Improve a vertex cover:
Use endpoints of the largest independent edge set of g as a starting point:
ApproximateVertexCover works with undirected graphs:
Directed graphs:
Multigraphs:
Mixed graphs:
ApproximateVertexCover works with large graphs:
Options (2)
Method (2)
The dynamic greedy heuristic is the default for relatively small graphs:
Method→"IndexedHeap" is most advantageous for larger graphs, for which it is the default:
For relatively smaller graphs, Method→"Greedy" can be faster, while giving a comparable cover:
Method→"GreedyStatic" is faster for both small and large graphs, at the expense of giving somewhat larger covers:
Properties and Relations (7)
The result of ApproximateVertexCover can be tested by VertexCoverQ:
ApproximateVertexCover may return results similar to FindVertexCover:
However, it does this in less time:
However, ApproximateVertexCover may also return covers of a larger size compared to FindVertexCover:
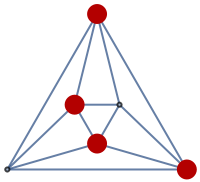
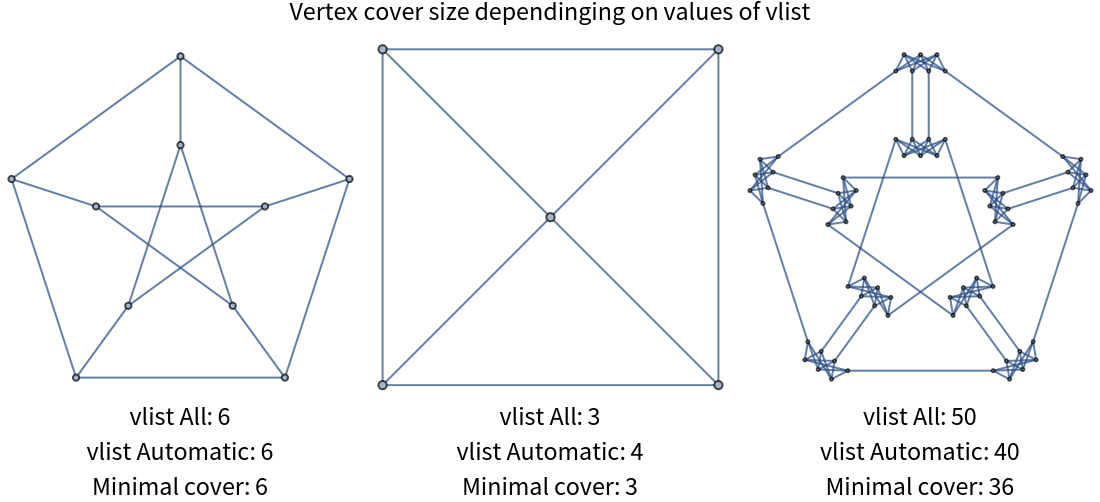
Using the Automatic value for vlist may give a smaller cover:
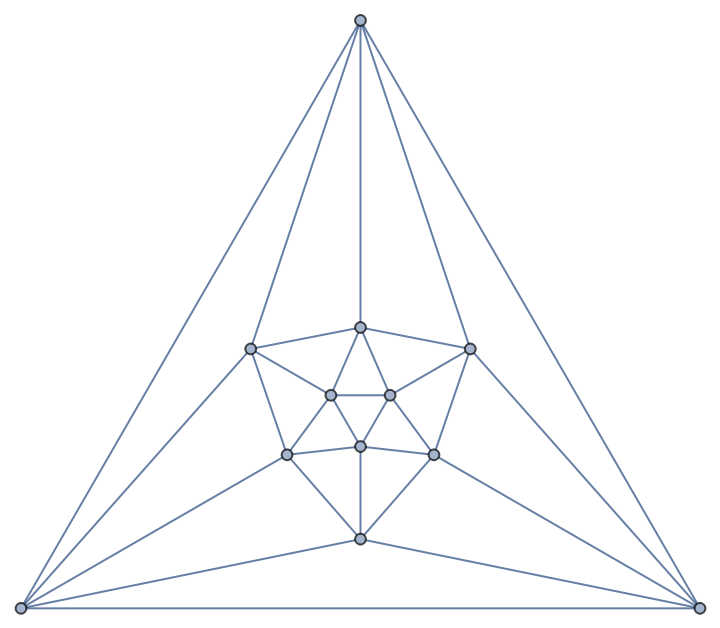
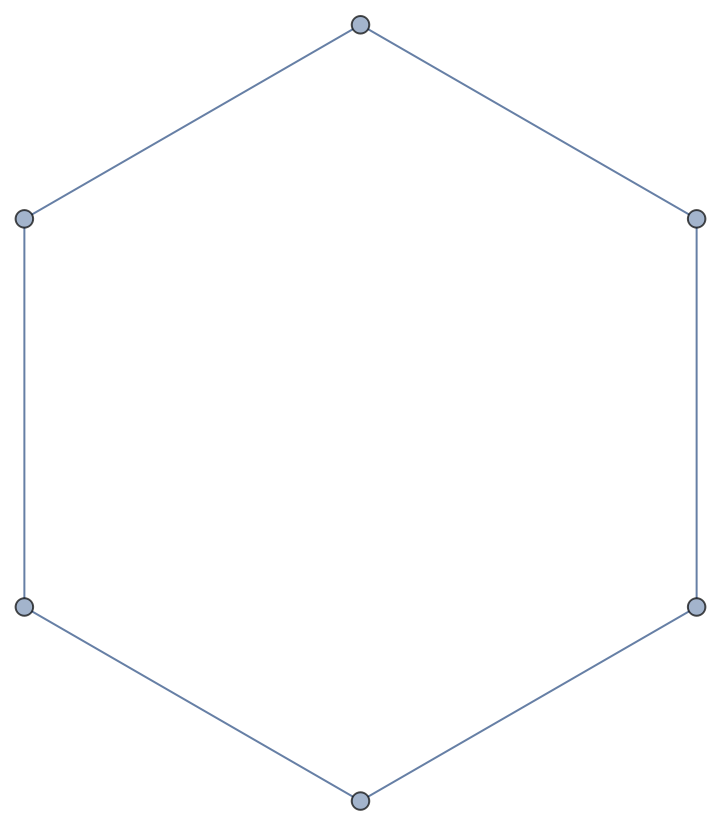
ApproximateVertexCover[g,All] may return covers that are equivalent, smaller or larger than ones given by ApproximateVertexCover[g,Automatic]:
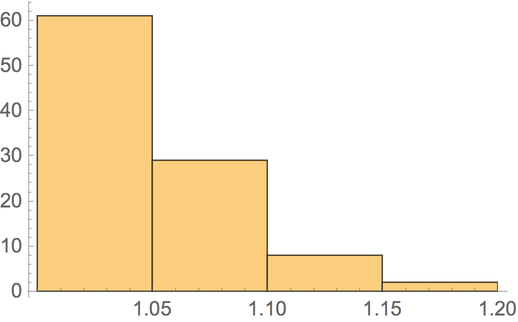
Although the algorithm in ApproximateVertexCover[g,Automatic] is guaranteed to give results not exceeding the minimal size by a factor of two, in practice the difference is often smaller:
Similarly, although ApproximateVertexCover[g] comes with no performance guarantees, in practice it often gives results that are not much worse than the minimal:
Possible Issues (2)
ApproximateVertexCover[g,{v1,v2,…}] works only if {v1,v2,…} is a vertex cover:
If you do not have a suitable vertex cover to improve, try using ApproximateVertexCover[g] without vlist:

![ResourceFunction["ApproximateVertexCover"][\!\(\*
GraphicsBox[
NamespaceBox["NetworkGraphics",
DynamicModuleBox[{Typeset`graph = HoldComplete[
Graph[{1, 2, 3, 6, 4, 5}, {Null, {{1, 2}, {1, 3}, {3, 4}, {5, 4}, {6, 1}, {6, 5}, {
4, 1}}}, {EdgeStyle -> {
Arrowheads[0.05]}, VertexShapeFunction -> {"Name"}}]], Typeset`boxes, Typeset`boxes$s2d = GraphicsGroupBox[{{
Directive[
Hue[0.6, 0.2, 0.8],
EdgeForm[
Directive[
GrayLevel[0],
Opacity[0.7]]]],
TagBox[
InsetBox[
BoxData[
FormBox[
PaneBox["1", Alignment -> Center, ImageMargins -> 2], TraditionalForm]], {0.9105692615187663, 0.8360540621313554}, BaseStyle -> "Graphics"], "DynamicName", BoxID -> "VertexID$1"],
TagBox[
InsetBox[
BoxData[
FormBox[
PaneBox["2", Alignment -> Center, ImageMargins -> 2], TraditionalForm]], {0., 1.1532590624791177`}, BaseStyle -> "Graphics"], "DynamicName", BoxID -> "VertexID$2"],
TagBox[
InsetBox[
BoxData[
FormBox[
PaneBox["3", Alignment -> Center, ImageMargins -> 2], TraditionalForm]], {0.9901787089965595, 0.}, BaseStyle -> "Graphics"], "DynamicName", BoxID -> "VertexID$3"],
TagBox[
InsetBox[
BoxData[
FormBox[
PaneBox["6", Alignment -> Center, ImageMargins -> 2], TraditionalForm]], {1.6310911016266327`, 0.3899112848656986}, BaseStyle -> "Graphics"], "DynamicName", BoxID -> "VertexID$4"],
TagBox[
InsetBox[
BoxData[
FormBox[
PaneBox["4", Alignment -> Center, ImageMargins -> 2], TraditionalForm]], {2.2927686727030645`, 0.9445770975677718}, BaseStyle -> "Graphics"], "DynamicName", BoxID -> "VertexID$5"],
TagBox[
InsetBox[
BoxData[
FormBox[
PaneBox["5", Alignment -> Center, ImageMargins -> 2], TraditionalForm]], {1.6608421533285063`, 1.4124733715227413`}, BaseStyle -> "Graphics"], "DynamicName", BoxID -> "VertexID$6"]}, {
Directive[
Opacity[0.7],
Hue[0.6, 0.7, 0.5]],
StyleBox[
LineBox[{
DynamicLocation["VertexID$1", Automatic, Center],
DynamicLocation["VertexID$2", Automatic, Center]}],
Arrowheads[0.05], StripOnInput -> False],
StyleBox[
LineBox[{
DynamicLocation["VertexID$1", Automatic, Center],
DynamicLocation["VertexID$3", Automatic, Center]}],
Arrowheads[0.05], StripOnInput -> False],
StyleBox[
LineBox[{
DynamicLocation["VertexID$1", Automatic, Center],
DynamicLocation["VertexID$6", Automatic, Center]}],
Arrowheads[0.05], StripOnInput -> False],
StyleBox[
LineBox[{
DynamicLocation["VertexID$1", Automatic, Center],
DynamicLocation["VertexID$4", Automatic, Center]}],
Arrowheads[0.05], StripOnInput -> False],
StyleBox[
LineBox[{
DynamicLocation["VertexID$3", Automatic, Center],
DynamicLocation["VertexID$4", Automatic, Center]}],
Arrowheads[0.05], StripOnInput -> False],
StyleBox[
LineBox[{
DynamicLocation["VertexID$4", Automatic, Center],
DynamicLocation["VertexID$5", Automatic, Center]}],
Arrowheads[0.05], StripOnInput -> False],
StyleBox[
LineBox[{
DynamicLocation["VertexID$5", Automatic, Center],
DynamicLocation["VertexID$6", Automatic, Center]}],
Arrowheads[0.05], StripOnInput -> False]}}], Typeset`data},
TagBox[
DynamicBox[GraphComputation`NetworkGraphicsBox[
2, Typeset`graph, Typeset`boxes], {CachedValue :> Typeset`boxes, SingleEvaluation -> True, SynchronousUpdating -> False, TrackedSymbols :> {}},
ImageSizeCache->{{0., 100.}, {-39.445019356085, 35.}}],
MouseAppearanceTag["NetworkGraphics"]],
AllowKernelInitialization->False,
UnsavedVariables:>{Typeset`data}]],
DefaultBaseStyle->{"NetworkGraphics", FrontEnd`GraphicsHighlightColor -> Hue[0.8, 1., 0.6]},
FrameTicks->None]\)]](https://www.wolframcloud.com/obj/resourcesystem/images/c6a/c6a75db3-d262-4a4a-b42f-a61b273d5357/43b2a2e22258265c.png)
![ResourceFunction["ApproximateVertexCover"][\!\(\*
GraphicsBox[
NamespaceBox["NetworkGraphics",
DynamicModuleBox[{Typeset`graph = HoldComplete[
Graph[{1, 3, 2, 6, 4, 5}, {{{1, 2}, {3, 1}, {2, 4}, {5, 4}, {1, 6}, {6, 5}, {4, 1}},
Null}, {EdgeStyle -> {
Arrowheads[0.08]}, PerformanceGoal -> "Quality", VertexShapeFunction -> {"Name"}}]], Typeset`boxes, Typeset`boxes$s2d = GraphicsGroupBox[{{
Arrowheads[0.03036417203345085],
Directive[
Opacity[0.7],
Hue[0.6, 0.7, 0.5]],
Arrowheads[0.08],
ArrowBox[{{
DynamicLocation["VertexID$1", Automatic, Center],
DynamicLocation["VertexID$2", Automatic, Center]}, {
DynamicLocation[
"VertexID$1", Automatic, Center],
DynamicLocation["VertexID$6", Automatic, Center]}, {
DynamicLocation[
"VertexID$2", Automatic, Center],
DynamicLocation["VertexID$4", Automatic, Center]}, {
DynamicLocation[
"VertexID$3", Automatic, Center],
DynamicLocation["VertexID$1", Automatic, Center]}, {
DynamicLocation[
"VertexID$4", Automatic, Center],
DynamicLocation["VertexID$1", Automatic, Center]}, {
DynamicLocation[
"VertexID$5", Automatic, Center],
DynamicLocation["VertexID$4", Automatic, Center]}, {
DynamicLocation[
"VertexID$6", Automatic, Center],
DynamicLocation["VertexID$5", Automatic, Center]}}]}, {
Directive[
Hue[0.6, 0.2, 0.8],
EdgeForm[
Directive[
GrayLevel[0],
Opacity[0.7]]]],
TagBox[
InsetBox[
BoxData[
FormBox[
PaneBox["1", Alignment -> Center, ImageMargins -> 2], TraditionalForm]], {1.0582418052620635`, 0.9723829770648784}, BaseStyle -> "Graphics"], "DynamicName", BoxID -> "VertexID$1"],
TagBox[
InsetBox[
BoxData[
FormBox[
PaneBox["3", Alignment -> Center, ImageMargins -> 2], TraditionalForm]], {1.1509423444907019`, 0.}, BaseStyle -> "Graphics"], "DynamicName", BoxID -> "VertexID$2"],
TagBox[
InsetBox[
BoxData[
FormBox[
PaneBox["2", Alignment -> Center, ImageMargins -> 2], TraditionalForm]], {0., 1.3421036772670925`}, BaseStyle -> "Graphics"], "DynamicName", BoxID -> "VertexID$3"],
TagBox[
InsetBox[
BoxData[
FormBox[
PaneBox["6", Alignment -> Center, ImageMargins -> 2], TraditionalForm]], {1.8963933008738443`, 0.45375950808317184`}, BaseStyle -> "Graphics"], "DynamicName", BoxID -> "VertexID$4"],
TagBox[
InsetBox[
BoxData[
FormBox[
PaneBox["4", Alignment -> Center, ImageMargins -> 2], TraditionalForm]], {2.666069013196534, 1.099186522746214}, BaseStyle -> "Graphics"], "DynamicName", BoxID -> "VertexID$5"],
TagBox[
InsetBox[
BoxData[
FormBox[
PaneBox["5", Alignment -> Center, ImageMargins -> 2], TraditionalForm]], {1.9309095855504228`, 1.6429177863358628`}, BaseStyle -> "Graphics"], "DynamicName", BoxID -> "VertexID$6"]}}], $CellContext`flag},
TagBox[
DynamicBox[GraphComputation`NetworkGraphicsBox[
3, Typeset`graph, Typeset`boxes, $CellContext`flag], {CachedValue :> Typeset`boxes, SingleEvaluation -> True, SynchronousUpdating -> False, TrackedSymbols :> {$CellContext`flag}},
ImageSizeCache->{{0., 99.99999999999999}, {-39.460905189751635`, 34.99999999999999}}],
MouseAppearanceTag["NetworkGraphics"]],
AllowKernelInitialization->False,
UnsavedVariables:>{$CellContext`flag}]],
DefaultBaseStyle->{"NetworkGraphics", FrontEnd`GraphicsHighlightColor -> Hue[0.8, 1., 0.6]},
FrameTicks->None,
GridLinesStyle->Directive[
GrayLevel[0.5, 0.4]]]\)]](https://www.wolframcloud.com/obj/resourcesystem/images/c6a/c6a75db3-d262-4a4a-b42f-a61b273d5357/1e045fc1edc656e4.png)
![ResourceFunction["ApproximateVertexCover"][\!\(\*
GraphicsBox[
NamespaceBox["NetworkGraphics",
DynamicModuleBox[{Typeset`graph = HoldComplete[
Graph[{1, 2, 3, 6, 4, 5}, {Null, {{1, 2}, {1, 3}, {1, 3}, {3, 4}, {5, 4}, {6, 1}, {
6, 5}, {6, 5}, {6, 5}, {4, 1}}}, {PerformanceGoal -> "Quality", VertexShapeFunction -> {"Name"}}]], Typeset`boxes, Typeset`boxes$s2d = GraphicsGroupBox[{{
Directive[
Opacity[0.7],
Hue[0.6, 0.7, 0.5]],
LineBox[{
DynamicLocation["VertexID$1", Automatic, Center],
DynamicLocation["VertexID$2", Automatic, Center]}],
BezierCurveBox[{
DynamicLocation["VertexID$1", Automatic, Center], {
1.2392731250755065`, 0.4989317964745188},
DynamicLocation["VertexID$3", Automatic, Center]}],
BezierCurveBox[{
DynamicLocation["VertexID$1", Automatic, Center], {
0.9712794857327156, 0.473422495739029},
DynamicLocation["VertexID$3", Automatic, Center]}],
LineBox[{
DynamicLocation["VertexID$1", Automatic, Center],
DynamicLocation["VertexID$4", Automatic, Center]}],
LineBox[{
DynamicLocation["VertexID$1", Automatic, Center],
DynamicLocation["VertexID$6", Automatic, Center]}],
LineBox[{
DynamicLocation["VertexID$3", Automatic, Center],
DynamicLocation["VertexID$4", Automatic, Center]}],
LineBox[{
DynamicLocation["VertexID$4", Automatic, Center],
DynamicLocation["VertexID$5", Automatic, Center]}],
BezierCurveBox[{
DynamicLocation["VertexID$5", Automatic, Center], {
2.2241662799347686`, 1.2693218513959759`},
DynamicLocation["VertexID$6", Automatic, Center]}],
LineBox[{
DynamicLocation["VertexID$5", Automatic, Center],
DynamicLocation["VertexID$6", Automatic, Center]}],
BezierCurveBox[{
DynamicLocation["VertexID$5", Automatic, Center], {
2.3741350699379584`, 1.4718850501139134`},
DynamicLocation["VertexID$6", Automatic, Center]}]}, {
Directive[
Hue[0.6, 0.2, 0.8],
EdgeForm[
Directive[
GrayLevel[0],
Opacity[0.7]]]],
TagBox[
InsetBox[
BoxData[
FormBox[
PaneBox["1", Alignment -> Center, ImageMargins -> 2], TraditionalForm]], {1.0589989420264807`, 0.9723542922135481}, BaseStyle -> "Graphics"], "DynamicName", BoxID -> "VertexID$1"],
TagBox[
InsetBox[
BoxData[
FormBox[
PaneBox["2", Alignment -> Center, ImageMargins -> 2], TraditionalForm]], {0., 1.341296311513045}, BaseStyle -> "Graphics"], "DynamicName", BoxID -> "VertexID$2"],
TagBox[
InsetBox[
BoxData[
FormBox[
PaneBox["3", Alignment -> Center, ImageMargins -> 2], TraditionalForm]], {1.1515536687817411`, 0.}, BaseStyle -> "Graphics"], "DynamicName", BoxID -> "VertexID$3"],
TagBox[
InsetBox[
BoxData[
FormBox[
PaneBox["6", Alignment -> Center, ImageMargins -> 2], TraditionalForm]], {1.897002425339307, 0.4534755453702776}, BaseStyle -> "Graphics"], "DynamicName", BoxID -> "VertexID$4"],
TagBox[
InsetBox[
BoxData[
FormBox[
PaneBox["4", Alignment -> Center, ImageMargins -> 2], TraditionalForm]], {2.6666280452965543`, 1.0985395371947577`}, BaseStyle -> "Graphics"], "DynamicName", BoxID -> "VertexID$5"],
TagBox[
InsetBox[
BoxData[
FormBox[
PaneBox["5", Alignment -> Center, ImageMargins -> 2], TraditionalForm]], {1.9316733045761725`, 1.6426673643151313`}, BaseStyle -> "Graphics"], "DynamicName", BoxID -> "VertexID$6"]}}], $CellContext`flag},
TagBox[
DynamicBox[GraphComputation`NetworkGraphicsBox[
3, Typeset`graph, Typeset`boxes, $CellContext`flag], {CachedValue :> Typeset`boxes, SingleEvaluation -> True, SynchronousUpdating -> False, TrackedSymbols :> {$CellContext`flag}},
ImageSizeCache->{{0., 100.00000000000001`}, {-39.44082649589048, 35.}}],
MouseAppearanceTag["NetworkGraphics"]],
AllowKernelInitialization->False,
UnsavedVariables:>{$CellContext`flag}]],
DefaultBaseStyle->{"NetworkGraphics", FrontEnd`GraphicsHighlightColor -> Hue[0.8, 1., 0.6]},
FrameTicks->None,
GridLinesStyle->Directive[
GrayLevel[0.5, 0.4]]]\)]](https://www.wolframcloud.com/obj/resourcesystem/images/c6a/c6a75db3-d262-4a4a-b42f-a61b273d5357/697206048a2eef72.png)
![ResourceFunction["ApproximateVertexCover"][\!\(\*
GraphicsBox[
NamespaceBox["NetworkGraphics",
DynamicModuleBox[{Typeset`graph = HoldComplete[
Graph[{1, 3, 2, 6, 4, 5}, {{{1, 2}, {3, 1}, {2, 4}}, {{5, 4}, {1, 6}, {6, 5}, {4, 1}}}, {EdgeStyle -> {
Arrowheads[0.08]}, PerformanceGoal -> "Quality", VertexShapeFunction -> {"Name"}}]], Typeset`boxes, Typeset`boxes$s2d = GraphicsGroupBox[{{
Arrowheads[0.03036225639824664],
Directive[
Opacity[0.7],
Hue[0.6, 0.7, 0.5]],
Arrowheads[0.08],
LineBox[{
DynamicLocation["VertexID$1", Automatic, Center],
DynamicLocation["VertexID$4", Automatic, Center]}],
LineBox[{
DynamicLocation["VertexID$1", Automatic, Center],
DynamicLocation["VertexID$6", Automatic, Center]}],
ArrowBox[{
DynamicLocation["VertexID$1", Automatic, Center],
DynamicLocation["VertexID$2", Automatic, Center]}],
ArrowBox[{
DynamicLocation["VertexID$2", Automatic, Center],
DynamicLocation["VertexID$4", Automatic, Center]}],
ArrowBox[{
DynamicLocation["VertexID$3", Automatic, Center],
DynamicLocation["VertexID$1", Automatic, Center]}],
LineBox[{
DynamicLocation["VertexID$4", Automatic, Center],
DynamicLocation["VertexID$5", Automatic, Center]}],
LineBox[{
DynamicLocation["VertexID$5", Automatic, Center],
DynamicLocation["VertexID$6", Automatic, Center]}]}, {
Directive[
Hue[0.6, 0.2, 0.8],
EdgeForm[
Directive[
GrayLevel[0],
Opacity[0.7]]]],
TagBox[
InsetBox[
BoxData[
FormBox[
PaneBox["1", Alignment -> Center, ImageMargins -> 2], TraditionalForm]], {1.0584185461609268`, 0.9722706650009502}, BaseStyle -> "Graphics"], "DynamicName", BoxID -> "VertexID$1"],
TagBox[
InsetBox[
BoxData[
FormBox[
PaneBox["3", Alignment -> Center, ImageMargins -> 2], TraditionalForm]], {1.1511230006050828`, 0.}, BaseStyle -> "Graphics"], "DynamicName", BoxID -> "VertexID$2"],
TagBox[
InsetBox[
BoxData[
FormBox[
PaneBox["2", Alignment -> Center, ImageMargins -> 2], TraditionalForm]], {0., 1.3418307911430136`}, BaseStyle -> "Graphics"], "DynamicName", BoxID -> "VertexID$3"],
TagBox[
InsetBox[
BoxData[
FormBox[
PaneBox["6", Alignment -> Center, ImageMargins -> 2], TraditionalForm]], {1.8966497904439512`, 0.4537055162293067}, BaseStyle -> "Graphics"], "DynamicName", BoxID -> "VertexID$4"],
TagBox[
InsetBox[
BoxData[
FormBox[
PaneBox["4", Alignment -> Center, ImageMargins -> 2], TraditionalForm]], {2.6664901555059592`, 1.098927115783615}, BaseStyle -> "Graphics"], "DynamicName", BoxID -> "VertexID$5"],
TagBox[
InsetBox[
BoxData[
FormBox[
PaneBox["5", Alignment -> Center, ImageMargins -> 2], TraditionalForm]], {1.931325145715449, 1.6424972585468378`}, BaseStyle -> "Graphics"], "DynamicName", BoxID -> "VertexID$6"]}}], $CellContext`flag},
TagBox[
DynamicBox[GraphComputation`NetworkGraphicsBox[
3, Typeset`graph, Typeset`boxes, $CellContext`flag], {CachedValue :> Typeset`boxes, SingleEvaluation -> True, SynchronousUpdating -> False, TrackedSymbols :> {$CellContext`flag}},
ImageSizeCache->{{0., 100.00000000000003`}, {-39.437952007426816`, 35.}}],
MouseAppearanceTag["NetworkGraphics"]],
AllowKernelInitialization->False,
UnsavedVariables:>{$CellContext`flag}]],
DefaultBaseStyle->{"NetworkGraphics", FrontEnd`GraphicsHighlightColor -> Hue[0.8, 1., 0.6]},
FrameTicks->None,
GridLinesStyle->Directive[
GrayLevel[0.5, 0.4]]]\)]](https://www.wolframcloud.com/obj/resourcesystem/images/c6a/c6a75db3-d262-4a4a-b42f-a61b273d5357/64883eed1809f428.png)


![cover = ResourceFunction["ApproximateVertexCover"][g];
ResourceFunction["ApproximateVertexCover"][g, Method -> "IndexedHeap"] === cover](https://www.wolframcloud.com/obj/resourcesystem/images/c6a/c6a75db3-d262-4a4a-b42f-a61b273d5357/34660a4b564b299d.png)
![g = RandomGraph[{1000, 10000}];
{t1, c1} = Timing[ResourceFunction["ApproximateVertexCover"][g, Method -> "Greedy"]];
{t2, c2} = Timing[ResourceFunction["ApproximateVertexCover"][g, Method -> "IndexedHeap"]];
{t1, t2}](https://www.wolframcloud.com/obj/resourcesystem/images/c6a/c6a75db3-d262-4a4a-b42f-a61b273d5357/12088a5534fc25ec.png)

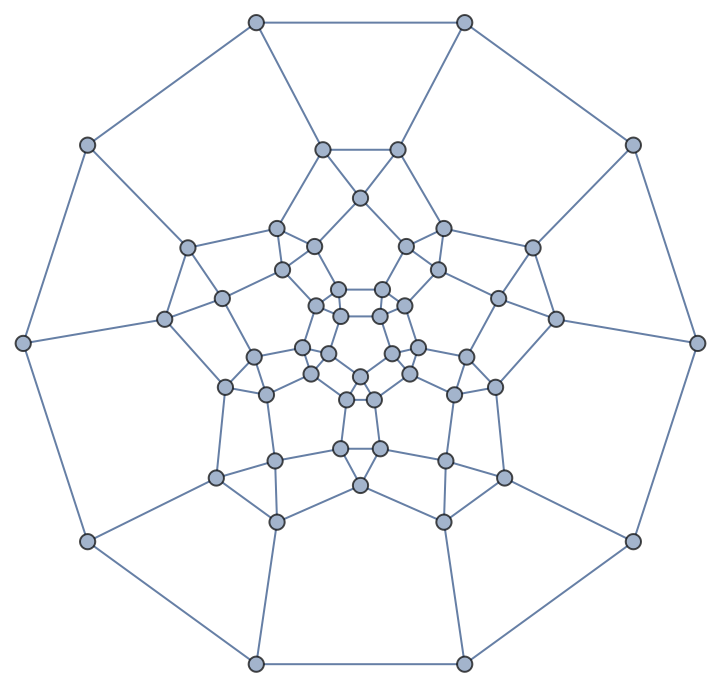
![Labeled[Grid[
Transpose[
Function[g, Flatten[{g, "vlist " <> ToString[#] <> ": " <> ToString[
Length[ResourceFunction["ApproximateVertexCover"][
g, #]]] & /@ {All, Automatic}, "Minimal cover: " <> ToString[Length[FindVertexCover[g]]]}]] /@ {PetersenGraph[5, 2], GraphData[{"Wheel", 5}], GraphData[
"MeredithGraph"]}]], "Vertex cover size dependinging on values of vlist" , Top]](https://www.wolframcloud.com/obj/resourcesystem/images/c6a/c6a75db3-d262-4a4a-b42f-a61b273d5357/5ddf2b55be378fe6.png)
![Histogram[
Length[ResourceFunction["ApproximateVertexCover"][#]]/
Length[FindVertexCover[#]] & /@ RandomGraph[{20, 40}, 100]]](https://www.wolframcloud.com/obj/resourcesystem/images/c6a/c6a75db3-d262-4a4a-b42f-a61b273d5357/6e7855768c1c12cd.png)
![g = \!\(\*
GraphicsBox[
NamespaceBox["NetworkGraphics",
DynamicModuleBox[{Typeset`graph = HoldComplete[
Graph[{1, 2, 3, 4, 5, 6, 7, 8}, {Null, {{1, 2}, {1, 4}, {1, 5}, {2, 3}, {2, 6}, {3, 4}, {
3, 7}, {4, 8}, {5, 6}, {5, 8}, {6, 7}, {7, 8}}}, {VertexShapeFunction -> {"Name"}, VertexCoordinates -> {{1., 6.123233995736766*^-17}, {
1.2246467991473532`*^-16, -1.}, {-1., -1.8369701987210297`*^-16}, {-2.4492935982947064`*^-16, 1.}, {2., 1.2246467991473532`*^-16}, {
2.4492935982947064`*^-16, -2.}, {-2., -3.6739403974420594`*^-16}, {-4.898587196589413*^-16, 2.}}}]], Typeset`boxes, Typeset`boxes$s2d = GraphicsGroupBox[{{
Directive[
Opacity[0.7],
Hue[0.6, 0.7, 0.5]],
LineBox[{{
DynamicLocation["VertexID$1", Automatic, Center],
DynamicLocation["VertexID$2", Automatic, Center]}, {
DynamicLocation[
"VertexID$1", Automatic, Center],
DynamicLocation["VertexID$4", Automatic, Center]}, {
DynamicLocation[
"VertexID$1", Automatic, Center],
DynamicLocation["VertexID$5", Automatic, Center]}, {
DynamicLocation[
"VertexID$2", Automatic, Center],
DynamicLocation["VertexID$3", Automatic, Center]}, {
DynamicLocation[
"VertexID$2", Automatic, Center],
DynamicLocation["VertexID$6", Automatic, Center]}, {
DynamicLocation[
"VertexID$3", Automatic, Center],
DynamicLocation["VertexID$4", Automatic, Center]}, {
DynamicLocation[
"VertexID$3", Automatic, Center],
DynamicLocation["VertexID$7", Automatic, Center]}, {
DynamicLocation[
"VertexID$4", Automatic, Center],
DynamicLocation["VertexID$8", Automatic, Center]}, {
DynamicLocation[
"VertexID$5", Automatic, Center],
DynamicLocation["VertexID$6", Automatic, Center]}, {
DynamicLocation[
"VertexID$5", Automatic, Center],
DynamicLocation["VertexID$8", Automatic, Center]}, {
DynamicLocation[
"VertexID$6", Automatic, Center],
DynamicLocation["VertexID$7", Automatic, Center]}, {
DynamicLocation[
"VertexID$7", Automatic, Center],
DynamicLocation["VertexID$8", Automatic, Center]}}]}, {
Directive[
Hue[0.6, 0.2, 0.8],
EdgeForm[
Directive[
GrayLevel[0],
Opacity[0.7]]]],
TagBox[
InsetBox[
BoxData[
FormBox[
PaneBox["1", Alignment -> Center, ImageMargins -> 2], TraditionalForm]], {1., 6.123233995736766*^-17}, BaseStyle -> "Graphics"], "DynamicName", BoxID -> "VertexID$1"],
TagBox[
InsetBox[
BoxData[
FormBox[
PaneBox["2", Alignment -> Center, ImageMargins -> 2], TraditionalForm]], {1.2246467991473532`*^-16, -1.}, BaseStyle -> "Graphics"], "DynamicName", BoxID -> "VertexID$2"],
TagBox[
InsetBox[
BoxData[
FormBox[
PaneBox["3", Alignment -> Center, ImageMargins -> 2], TraditionalForm]], {-1., -1.8369701987210297`*^-16}, BaseStyle -> "Graphics"], "DynamicName", BoxID -> "VertexID$3"],
TagBox[
InsetBox[
BoxData[
FormBox[
PaneBox["4", Alignment -> Center, ImageMargins -> 2], TraditionalForm]], {-2.4492935982947064`*^-16, 1.}, BaseStyle -> "Graphics"], "DynamicName", BoxID -> "VertexID$4"],
TagBox[
InsetBox[
BoxData[
FormBox[
PaneBox["5", Alignment -> Center, ImageMargins -> 2], TraditionalForm]], {2., 1.2246467991473532`*^-16}, BaseStyle -> "Graphics"], "DynamicName", BoxID -> "VertexID$5"],
TagBox[
InsetBox[
BoxData[
FormBox[
PaneBox["6", Alignment -> Center, ImageMargins -> 2], TraditionalForm]], {2.4492935982947064`*^-16, -2.}, BaseStyle -> "Graphics"], "DynamicName", BoxID -> "VertexID$6"],
TagBox[
InsetBox[
BoxData[
FormBox[
PaneBox["7", Alignment -> Center, ImageMargins -> 2], TraditionalForm]], {-2., -3.6739403974420594`*^-16}, BaseStyle -> "Graphics"], "DynamicName", BoxID -> "VertexID$7"],
TagBox[
InsetBox[
BoxData[
FormBox[
PaneBox["8", Alignment -> Center, ImageMargins -> 2], TraditionalForm]], {-4.898587196589413*^-16, 2.}, BaseStyle -> "Graphics"], "DynamicName", BoxID -> "VertexID$8"]}}], Typeset`data},
TagBox[
DynamicBox[GraphComputation`NetworkGraphicsBox[
2, Typeset`graph, Typeset`boxes], {CachedValue :> Typeset`boxes, SingleEvaluation -> True, SynchronousUpdating -> False, TrackedSymbols :> {}},
ImageSizeCache->{{0., 89.99999999999999}, {-52., 46.999999999999986`}}],
MouseAppearanceTag["NetworkGraphics"]],
AllowKernelInitialization->False,
UnsavedVariables:>{Typeset`data}]],
DefaultBaseStyle->{"NetworkGraphics", FrontEnd`GraphicsHighlightColor -> Hue[0.8, 1., 0.6]},
FrameTicks->None]\);](https://www.wolframcloud.com/obj/resourcesystem/images/c6a/c6a75db3-d262-4a4a-b42f-a61b273d5357/56595f6207d144df.png)
