Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Approximate the generalized Voronoi mesh for non-overlapping geometries
ResourceFunction["ApproximateGeneralizedVoronoiMesh"][{g1,g2,…}] gives a MeshRegion that approximates the Voronoi mesh of curves approximated by the 2D points in lists g1,g2,…. | |
ResourceFunction["ApproximateGeneralizedVoronoiMesh"][{g1,g2,…},{{xmin,xmax},{ymin,ymax}}] clips the mesh to the bounds [xmin,xmax]⨯ [ymin,ymax]. |
Generate the Voronoi mesh for some points, lines and a parabola:
| In[1]:= | ![With[
{parabola = Table[{t, 1.7 - t*t}, {t, -0.5, 0.5, 0.1}],
line1 = Table[{t, t}, {t, 0, 1, 0.1}],
line2 = Table[{t - 0.7, -0.5 - 0.1 t}, {t, 0, 1, 0.1}],
point1 = {1, 0}, point2 = {0, 1}},
Show[
ResourceFunction["ApproximateGeneralizedVoronoiMesh"][
{parabola, line1, line2, {point1}, {point2}},
{{-1, 2}, {-1, 2}}],
ListLinePlot[parabola],
ListLinePlot[line1],
ListLinePlot[line2],
ListPlot[{point1, point2}]]]](https://www.wolframcloud.com/obj/resourcesystem/images/534/53474a32-1410-4119-9721-cf9f07a21d68/36ec3d28529d41cf.png) |
| Out[1]= | 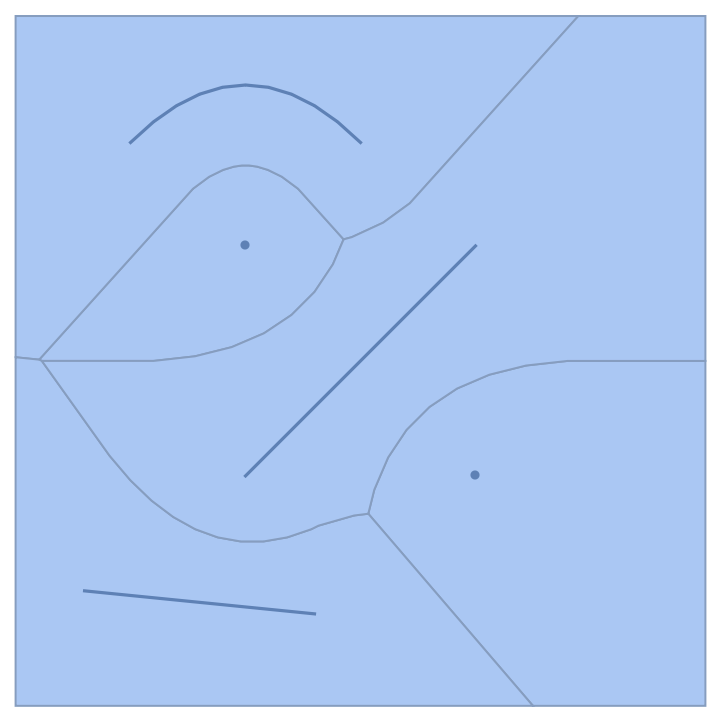 |
Since MeshRegion cannot contain polygons with holes, the Voronoi meshes which contain such polygons will contain edges so that such polygons can be represented without holes:
| In[2]:= | ![With[
{circle = Table[AngleVector[t], {t, 0, 2 Pi + 0.1, 0.1}],
point1 = {{-0.5, 0}},
point2 = {{0.5, 0}}},
Show[
ResourceFunction["ApproximateGeneralizedVoronoiMesh"][
{circle, point1, point2}, {{-1.2, 1.2}, {-1.2, 1.2}}],
ListLinePlot[circle],
ListPlot[point1],
ListPlot[point2]]]](https://www.wolframcloud.com/obj/resourcesystem/images/534/53474a32-1410-4119-9721-cf9f07a21d68/7872c7a2963cf6f9.png) |
| Out[2]= | 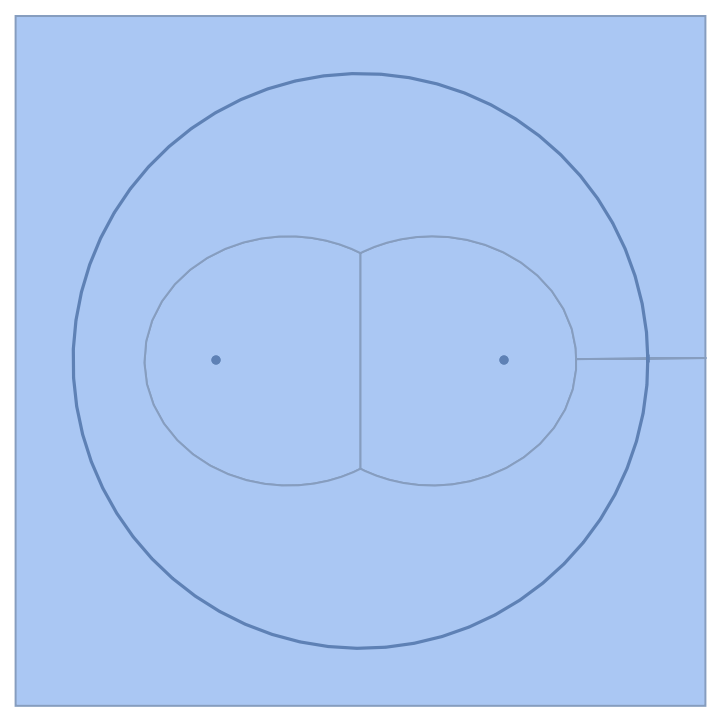 |
This work is licensed under a Creative Commons Attribution 4.0 International License