Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 AntidiagonalMatrixQ

Source Notebook

Tests whether a matrix is an antidiagonal matrix

Contributed by: Sander Huisman

ResourceFunction["AntidiagonalMatrixQ"][m]

gives True if m is antidiagonal, and False otherwise.

ResourceFunction["AntidiagonalMatrixQ"][m,k]

gives True if m has nonzero elements only on the kth antidiagonal, and False otherwise.

Details and Options

An antidiagonal matrix is defined as a matrix whose elements are zero except for its antidiagonal:
ResourceFunction["AntidiagonalMatrixQ"][m] works even if m is not square.
For positive k, ResourceFunction["AntidiagonalMatrixQ"][m,k] tests whether the antidiagonal is above the leading antidiagonal. ResourceFunction["AntidiagonalMatrixQ"][m,-k] tests whether the antidiagonal is below.
ResourceFunction["AntidiagonalMatrixQ"] works on SparseArray matrices.

Examples

Basic Examples (3) 

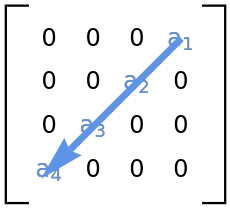
Check if a matrix is an antidiagonal matrix:

In[1]:=
ResourceFunction[ "AntidiagonalMatrixQ"][{{0, 0, 1}, {0, 3, 0}, {2, 0, 0}}]
Out[1]=

Test if the antidiagonal is above the leading antidiagonal one:

In[2]:=
ResourceFunction[ "AntidiagonalMatrixQ"][{{0, 2, 0}, {3, 0, 0}, {0, 0, 0}}, 1]
Out[2]=

An example of a matrix that is not antidiagonal:

In[3]:=
ResourceFunction[ "AntidiagonalMatrixQ"][{{0, 0, 1}, {0, 2, 0}, {3, 0, 0.1}}]
Out[3]=

Scope (3) 

Test a complex matrix:

In[4]:=
ResourceFunction["AntidiagonalMatrixQ"][{{0, 1. + I}, {2. - I, 0}}]
Out[4]=

Test a rectangular matrix:

In[5]:=
ResourceFunction["AntidiagonalMatrixQ"][{{0, 0, 0, 1}, {0, 0, 1, 0}}]
Out[5]=

Test a SparseArray matrix:

In[6]:=
ResourceFunction["AntidiagonalMatrixQ"][SparseArray[ Automatic, {2, 4}, 0, {1, {{0, 1, 2}, {{4}, {3}}}, {1, 1}}]]
Out[6]=

Options (1) 

Tolerance (1) 

Check if the off-antidiagonal elements are zero within a certain tolerance:

In[7]:=
ResourceFunction[ "AntidiagonalMatrixQ"][{{0, 1, 0.001}, {1, 0, 0}, {0, 0, 0}}, 1, Tolerance -> 0.01]
Out[7]=

Properties and Relations (1) 

If the expression is not a matrix, AntidiagonalMatrixQ will return False:

In[8]:=
ResourceFunction["AntidiagonalMatrixQ"][1]
Out[8]=
In[9]:=
ResourceFunction["AntidiagonalMatrixQ"][{1, 2, 3}]
Out[9]=

Publisher

SHuisman

Version History

  • 1.0.0 – 31 July 2019

Related Resources

License Information