Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Creates an antidiagonal matrix by given the antidiagonal
ResourceFunction["AntidiagonalMatrix"][list] gives a matrix with the elements of list on the leading antidiagonal, and 0 elsewhere. | |
ResourceFunction["AntidiagonalMatrix"][list,k] gives a matrix with the elements of list on the kth antidiagonal. | |
ResourceFunction["AntidiagonalMatrix"][list,k,n] pads with 0s to create an n×n matrix. |
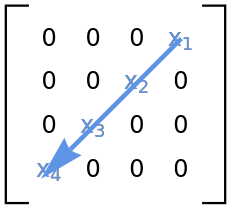
Construct an antidiagonal matrix:
| In[1]:= |
|
| Out[1]= |
|
A super-antidiagonal matrix:
| In[2]:= |
|
| Out[2]= |
|
A sub-antidiagonal matrix:
| In[3]:= |
|
| Out[3]= |
|
The elements in AntidiagonalMatrix are chosen to match the elements of the vector:
| In[4]:= |
|
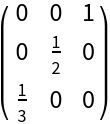
Exact number entries:
| In[5]:= |
|
| Out[5]= |
|
Machine-number entries:
| In[6]:= |
|
| Out[6]= |
|
Arbitrary-precision number entries:
| In[7]:= |
|
| Out[7]= |
|
When the vector is a SparseArray object, AntidiagonalMatrix will give a SparseArray object:
| In[8]:= |
|
| Out[8]= |
|
| In[9]:= |
|
| Out[9]= |
|
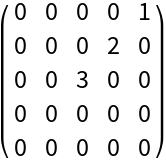
Pad with zeros to make a larger square matrix:
| In[10]:= |
|
| Out[10]= |
|
Make a square matrix with the specified dimension:
| In[11]:= |
|
| Out[11]= |
|
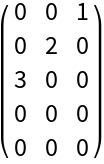
Rectangular diagonal matrices:
| In[12]:= |
|
| Out[12]= |
|
| In[13]:= |
|
| Out[13]= |
|
Express a matrix as the sum of its antidiagonal and off-antidiagonal parts:
| In[14]:= |
|
| Out[14]= |

|
| In[15]:= |
![md = ResourceFunction["AntidiagonalMatrix"][
ResourceFunction["Antidiagonal"][m]];
mo = m - md;
Map[MatrixForm, {md, mo}]](https://www.wolframcloud.com/obj/resourcesystem/images/515/515ac64e-7f70-4a46-b1af-540753dccd1b/79e261f829584a76.png)
|
| Out[17]= |
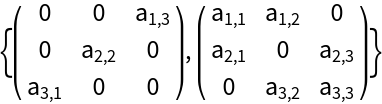
|
Construct a 5×5 tri-antidiagonal matrix:
| In[18]:= |
![n = 5;
MatrixForm[
ResourceFunction["AntidiagonalMatrix"][
Array[Subscript[a, #] &, n - 1], -1] + ResourceFunction["AntidiagonalMatrix"][
Array[Subscript[b, #] &, n]] + ResourceFunction["AntidiagonalMatrix"][
Array[Subscript[c, #] &, n - 1], 1]]](https://www.wolframcloud.com/obj/resourcesystem/images/515/515ac64e-7f70-4a46-b1af-540753dccd1b/2add920443a2195e.png)
|
| Out[19]= |

|
Extract the antidiagonal from an antidiagonal rectangular matrix:
| In[20]:= |
![m = ( {
{0, a},
{b, 0},
{0, 0}
} );
d = ResourceFunction["Antidiagonal"][m]](https://www.wolframcloud.com/obj/resourcesystem/images/515/515ac64e-7f70-4a46-b1af-540753dccd1b/1bd3e81220a3880a.png)
|
| Out[21]= |
|
Reconstruct the original matrix from the antidiagonal:
| In[22]:= |
|
| Out[22]= |
|
Using the resource function Antidiagonal with AntidiagonalMatrix gives the original vector:
| In[23]:= |
![v = RandomReal[1, 100];
ResourceFunction["Antidiagonal"][
ResourceFunction["AntidiagonalMatrix"][v]] === v](https://www.wolframcloud.com/obj/resourcesystem/images/515/515ac64e-7f70-4a46-b1af-540753dccd1b/66f9bebd4acbbdd3.png)
|
| Out[24]= |
|
This work is licensed under a Creative Commons Attribution 4.0 International License