Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 Antidiagonal

Source Notebook

Give the antidiagonal of a matrix

Contributed by: Sander Huisman

ResourceFunction["Antidiagonal"][m]

gives the list of elements on the leading antidiagonal of the matrix m.

ResourceFunction["Antidiagonal"][m,k]

gives the elements on the kth antidiagonal of m.

Details and Options

An antidiagonal is defined as a list of elements for which the sum of the indices are equal, where the first element is in the top-right of a matrix:
ResourceFunction["Antidiagonal"][m] works even if m is not square.
For positive k, ResourceFunction["Antidiagonal"][m,k] gives antidiagonals above the leading antidiagonal while ResourceFunction["Antidiagonal"][m,-k] gives antidiagonals below.
ResourceFunction["Antidiagonal"] works on SparseArray matrices and will return a SparseArray list.

Examples

Basic Examples (3) 

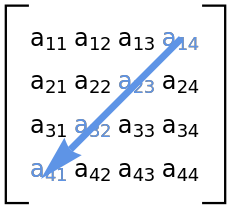
Give the antidiagonal elements of a matrix:

In[1]:=
ResourceFunction["Antidiagonal"][{{a, b, c}, {d, e, f}, {g, h, i}}]
Out[1]=

Give antidiagonals one element above and below the leading diagonal:

In[2]:=
ResourceFunction["Antidiagonal"][{{a, b, c}, {d, e, f}, {g, h, i}}, 1]
Out[2]=
In[3]:=
ResourceFunction[ "Antidiagonal"][{{a, b, c}, {d, e, f}, {g, h, i}}, -1]
Out[3]=

Give an antidiagonal of a nonsquare matrix:

In[4]:=
ResourceFunction[ "Antidiagonal"][{{1, 2, 3, 4}, {5, 6, 7, 8}, {9, 10, 11, 12}}]
Out[4]=

Properties and Relations (1) 

Antidiagonal and Diagonal are related to each other:

In[5]:=
m = {{a, b, c}, {d, e, f}, {g, h, i}}; ResourceFunction["Antidiagonal"][m] == Reverse[Diagonal[Reverse[m]]] == Diagonal[Reverse[m, 2]]
Out[6]=

Possible Issues (1) 

If k is too high or too low, an empty list is returned:

In[7]:=
ResourceFunction["Antidiagonal"][{{a, b, c}, {d, e, f}, {g, h, i}}, 3]
Out[7]=

Neat Examples (1) 

Rotate a matrix by 45 degrees:

In[8]:=
Row[Column[ ResourceFunction[ "Antidiagonal"][{{a, b, c}, {d, e, f}, {g, h, i}}, #]] & /@ Range[2, -2, -1]]
Out[8]=

Publisher

SHuisman

Version History

  • 1.0.0 – 24 June 2019

License Information