Details and Options
ResourceFunction["AntColonyOptimization"] is a global stochastic optimization method for the solution of combinatorial arrangement problems. It imitates the swarm communication behaviour of ants during foraging (Stigmergic Optimization).
The optimization is based on the exchange of information between individuals (randomly generated solutions) using a virtual pheromone trail for the information exchange.
ResourceFunction["AntColonyOptimization"] finds a solution of vector x, where the ith element of x is chosen from the values of the ith list in array, such that fitness[x] has the smallest positive value found.
The input
array takes a
List of lists with available values at each row. The lists need not have uniform length.
The fitness function to be minimized must return a positive scalar value. Therefore, the standard method of negating the objective function to convert a minimization problem into a maximization problem doesn’t work in this ACO implementation.
Limitation: This implementation does not consider dependencies of design variables among each other. The assignment of the design variables must be independent of the settings of the others. The definition of the search space is therefore possible using only a given array and does therefore not require a given tree or graph structure of the search space. Optimization problems such as the traveling salesman cannot be encoded in this way.
Optimization parameters given as options include:
| "PopulationSize" | 500 | number of ants |
| "MaxIterations" | 200 | maximum iterations |
| "FinishAtPheromoneThreshold" | 0.95 | stop criterion |
| "PheromoneFunction" | (1/#)& | pheromone concentration to be deposited depending on fitness |
| "WeatheringFactor" | 0.05 | fraction of decreasing pheromone concentration (selection probability) per iteration |
| "ProbabilitySelectBestPath" | 0.02 | proportion of generated solution alternatives that currently prefer the best solution |
The computation will stop if the selection probability for a variable state exceeds the value of "FinishAtPheromoneThreshold".
"PheromoneFunction" is a function whose result marks the selection probability for the next step. By default, larger fitness results receive lower marking values than smaller fitness results.
Optimization parameters control the runtime behavior and solution quality as a tradeoff between exploitation and exploration. These can be modified depending on the target function and the number of variables, e.g. by trial and error.
The option "ProbabilitySelectBestPath" takes values between zero and one. Smaller values use probabilistic selecting resulting in slower convergence but exploring more possibilities.
The current minimal selection probability for a variable state is monitored during the iterations. The smaller it is, the greater the ability to explore new solutions.
The output of
ResourceFunction["AntColonyOptimization"] is a
List representing the best found solution. Due to the stochastic search method, this optimum does not necessarily have to be global, thus better solutions may exist.
When the third argument is
All, the output is an
Association with keys:
| "Best" | variable allocation which minimizes fitness |
| "Iterations" | for each iteration step:
{arguments which minimize fitness,
normalized pheromone matrix,
and current minimal selection probability for a variable state} |
| "NumberOfFunctionCalls" | number of calls made to the fitness calls |
![SeedRandom[314];
possibValues = Table[RandomSample[Range[10]], {i, Range[10]}];
possibValues // Grid](https://www.wolframcloud.com/obj/resourcesystem/images/56f/56f50720-2827-4bd1-b4c3-d408569e3139/1f6ca5a8f7d4f07d.png)

![SeedRandom[314];
possibValues = Table[RandomSample[Range[10]], {i, Range[10]}];
fit[x_List] := Total[x]](https://www.wolframcloud.com/obj/resourcesystem/images/56f/56f50720-2827-4bd1-b4c3-d408569e3139/4a5ade5ad85b609a.png)
![Column@{ListLinePlot[fit /@ result["Iterations"][[All, 1]], PlotLabel -> "Fitness function", GridLines -> Automatic],
ListLinePlot[result["Iterations"][[All, 3]], PlotLabel -> "Min. pheromone concentration", GridLines -> Automatic]}](https://www.wolframcloud.com/obj/resourcesystem/images/56f/56f50720-2827-4bd1-b4c3-d408569e3139/6088407704e16af0.png)
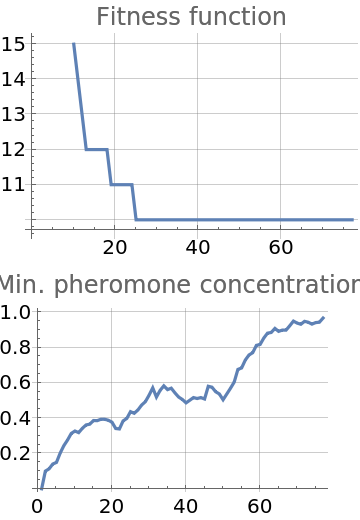

![ResourceFunction["AntColonyOptimization"][
Table[RandomSample[Range[10]], {i, Range[10]}], Total[#] &, All,
"PopulationSize" -> 500, "MaxIterations" -> 200, "FinishAtPheromoneThreshold" -> 0.95, "WeatheringFactor" -> 0.05, "PheromoneFunction" -> (1/# &), "ProbabilitySelectBestPath" -> 0.02];](https://www.wolframcloud.com/obj/resourcesystem/images/56f/56f50720-2827-4bd1-b4c3-d408569e3139/161f09bd3da3a247.png)
![ResourceFunction["AntColonyOptimization"][
Table[RandomSample[Range[10]], {i, Range[10]}], Total[#] &, All,
"PheromoneFunction" -> (1/(20 #) &)];](https://www.wolframcloud.com/obj/resourcesystem/images/56f/56f50720-2827-4bd1-b4c3-d408569e3139/2d9a5e997f2eb517.png)
![massError[coins_List] := Module[{eps = 10.^-6, error},
error = QuantityMagnitude[Abs@((Values[moneyMass] . coins) - mWallet), "Grams"];
If[(Total@coins) == 0,
10000.,
If[error <= eps, eps, error]]]](https://www.wolframcloud.com/obj/resourcesystem/images/56f/56f50720-2827-4bd1-b4c3-d408569e3139/70e4c01e48c7a353.png)
![possibCoins = Values@<|"1¢Range" -> Range[0, 5], "2¢Range" -> Range[0, 5], "5¢Range" -> Range[0, 5], "10¢Range" -> Range[0, 8], "20¢Range" -> Range[0, 7], "50¢Range" -> Range[0, 7], "1€Range" -> Range[0, 7], "2€Range" -> Range[0, 7]|>;
possibCoins // Grid](https://www.wolframcloud.com/obj/resourcesystem/images/56f/56f50720-2827-4bd1-b4c3-d408569e3139/7df5e3440fd806cf.png)

![Table[Values[
moneyMass] . (result = (ResourceFunction["AntColonyOptimization"][
possibCoins, massError, "PopulationSize" -> 1000, "FinishAtPheromoneThreshold" -> 0.99, "WeatheringFactor" -> 0.01, "MaxIterations" -> 30])) -> Values[moneyValue] . result,
{3}]](https://www.wolframcloud.com/obj/resourcesystem/images/56f/56f50720-2827-4bd1-b4c3-d408569e3139/594a174747531c6f.png)
![ResourceFunction["AntColonyOptimization"][
{
{4, 2, 3, 1, 5, 6},
{3, 1, 6, 4},
{6, 3, 4, 1, 2, 5},
{6},
{5, 6},
{2, 6, 1}
},
(Total[1/#] &)]](https://www.wolframcloud.com/obj/resourcesystem/images/56f/56f50720-2827-4bd1-b4c3-d408569e3139/17bb21f7985d31fe.png)

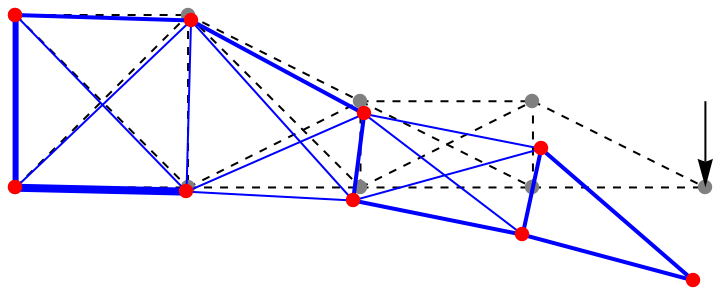
![objective[sections_] := With[{uMax = maxDeform, u18 = N@Abs@(computeDeformation[sections] // Last // Values), m = N@computeMass[sections]},
If[u18 > uMax, m + 250 (u18 - uMax)^2, m]
];](https://www.wolframcloud.com/obj/resourcesystem/images/56f/56f50720-2827-4bd1-b4c3-d408569e3139/35b62b1d20a4a7a4.png)
![result = ResourceFunction["AntColonyOptimization"][
ConstantArray[rodSectionsValid, Length@rodElements],
objective, "PopulationSize" -> 800, "MaxIterations" -> 20, "FinishAtPheromoneThreshold" -> 0.80];](https://www.wolframcloud.com/obj/resourcesystem/images/56f/56f50720-2827-4bd1-b4c3-d408569e3139/192589ece220d119.png)
![solUAll = Partition[{0, Subscript[u, 2], 0, 0, Subscript[u, 5], Subscript[u, 6], Subscript[u, 7], Subscript[u, 8], Subscript[u, 9], Subscript[
u, 10], Subscript[u, 11], Subscript[u, 12], Subscript[u, 13], Subscript[u, 14], Subscript[u, 15], Subscript[u, 16], Subscript[
u, 17], Subscript[u, 18]} /. Thread[{Subscript[u, 2], Subscript[u, 5], Subscript[u, 6], Subscript[u, 7], Subscript[u, 8], Subscript[u, 9], Subscript[u,
10], Subscript[u, 11], Subscript[u, 12], Subscript[u, 13], Subscript[u, 14], Subscript[u, 15], Subscript[u, 16], Subscript[u, 17], Subscript[u, 18]} -> Values[computeDeformation[result]][[4 ;; -1]]], 2];](https://www.wolframcloud.com/obj/resourcesystem/images/56f/56f50720-2827-4bd1-b4c3-d408569e3139/018a83a3452eddfd.png)
![structDeformed = Graphics[{rodElements /. {no_Integer, prop_List} :> {Blue, AbsoluteThickness[
prop[[3]] /. Table[Subscript[a, i] -> result[[i]]/10, {i, 18}]], Line[{defNodes[[prop[[1]], 2]], defNodes[[prop[[2]], 2]]}]}, defNodes /. {no_Integer, coord_List} -> {Hue[0], PointSize[0.02`],
Point[coord]}}, AspectRatio -> Automatic];](https://www.wolframcloud.com/obj/resourcesystem/images/56f/56f50720-2827-4bd1-b4c3-d408569e3139/6da061c27df56418.png)