Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 AncestralNestTree

Source Notebook

Grow Tree objects by iteratively adding children to leaves using information from their ancestors

Contributed by: Daniel McDonald

ResourceFunction["AncestralNestTree"][f,tree]

adds children to each leaf of tree, with f[{expr1,expr2,…}] giving the list of data for the new children of a leaf whose path from the root of tree goes through vertices having data expr1,expr2,… in order.

ResourceFunction["AncestralNestTree"][f,tree,n]

successively applies f to the data of each leaf up to level n, adding at most n levels to each leaf.

ResourceFunction["AncestralNestTree"][f,tree,n,h]

additionally applies h to the data of the new subtrees.

ResourceFunction["AncestralNestTree"][f,expr,…]

constructs a tree by nesting f on the tree leaf with data expr.

Details and Options

ResourceFunction["AncestralNestTree"] takes the same options as Tree.
ResourceFunction["AncestralNestTree"][f,tree] is equivalent to ResourceFunction["AncestralNestTree"][f,tree,1].

Examples

Basic Examples (2) 

Extend the leaves of a tree:

In[1]:=
ResourceFunction[ "AncestralNestTree", ResourceSystemBase -> "https://www.wolframcloud.com/obj/resourcesystem/api/1.0"][{f[#], g[#]} &, \!\(\* GraphicsBox[ NamespaceBox["Trees", DynamicModuleBox[{Typeset`tree = HoldComplete[ Tree[$CellContext`a, { Tree[$CellContext`b, None], Tree[$CellContext`c, None]}]]}, NamespaceBox[{ {Hue[0.6, 0.7, 0.5], Opacity[0.7], Arrowheads[Medium], {RGBColor[0.6, 0.5882352941176471, 0.5529411764705883], AbsoluteThickness[1], LineBox[{{0.4472135954999579, 0.8929961074943159}, {0., 0.}}]}, {RGBColor[0.6, 0.5882352941176471, 0.5529411764705883], AbsoluteThickness[1], LineBox[{{0.4472135954999579, 0.8929961074943159}, { 0.8944271909999159, 0.}}]}}, {Hue[0.6, 0.2, 0.8], EdgeForm[{GrayLevel[0], Opacity[0.7]}], TagBox[InsetBox[ FrameBox["a", Background->Directive[ RGBColor[0.9607843137254902, 0.9882352941176471, 0.9764705882352941]], BaseStyle->GrayLevel[0], FrameMargins->{{2, 2}, {1, 1}}, FrameStyle->Directive[ RGBColor[0.4196078431372549, 0.6313725490196078, 0.4196078431372549], AbsoluteThickness[1], Opacity[1]], ImageSize->Automatic, RoundingRadius->4, StripOnInput->False], {0.4472135954999579, 0.8929961074943159}], "DynamicName", BoxID -> "VertexID$1"], TagBox[InsetBox[ FrameBox["b", Background->Directive[ RGBColor[0.9607843137254902, 0.9882352941176471, 0.9764705882352941]], BaseStyle->GrayLevel[0], FrameMargins->{{2, 2}, {1, 1}}, FrameStyle->Directive[ RGBColor[0.4196078431372549, 0.6313725490196078, 0.4196078431372549], AbsoluteThickness[1], Opacity[1]], ImageSize->Automatic, RoundingRadius->0, StripOnInput->False], {0., 0.}], "DynamicName", BoxID -> "VertexID$2"], TagBox[InsetBox[ FrameBox["c", Background->Directive[ RGBColor[0.9607843137254902, 0.9882352941176471, 0.9764705882352941]], BaseStyle->GrayLevel[0], FrameMargins->{{2, 2}, {1, 1}}, FrameStyle->Directive[ RGBColor[0.4196078431372549, 0.6313725490196078, 0.4196078431372549], AbsoluteThickness[1], Opacity[1]], ImageSize->Automatic, RoundingRadius->0, StripOnInput->False], {0.8944271909999159, 0.}], "DynamicName", BoxID -> "VertexID$3"]}}]]], AlignmentPoint->Center, Axes->False, AxesLabel->None, AxesOrigin->Automatic, AxesStyle->{}, Background->None, BaseStyle->{}, BaselinePosition->Automatic, ContentSelectable->Automatic, DefaultBaseStyle->"TreeGraphics", DisplayFunction->Identity, Epilog->{}, FormatType->StandardForm, Frame->False, FrameLabel->None, FrameStyle->{}, FrameTicks->None, FrameTicksStyle->{}, GridLines->None, GridLinesStyle->{}, ImageMargins->0., ImagePadding->All, ImageSize->{39.522918701171875`, Automatic}, LabelStyle->{}, PlotLabel->None, PlotRange->All, PlotRangeClipping->False, PlotRangePadding->Automatic, PlotRegion->Automatic, Prolog->{}, RotateLabel->True, Ticks->Automatic, TicksStyle->{}]\)]
Out[1]=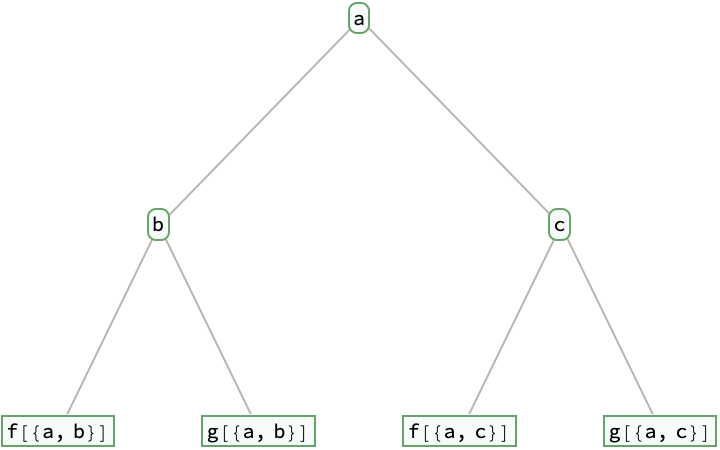

Build a tree from an expression:

In[2]:=
ResourceFunction[ "AncestralNestTree", ResourceSystemBase -> "https://www.wolframcloud.com/obj/resourcesystem/api/1.0"][f, x, 2]
Out[2]=

Options (1) 

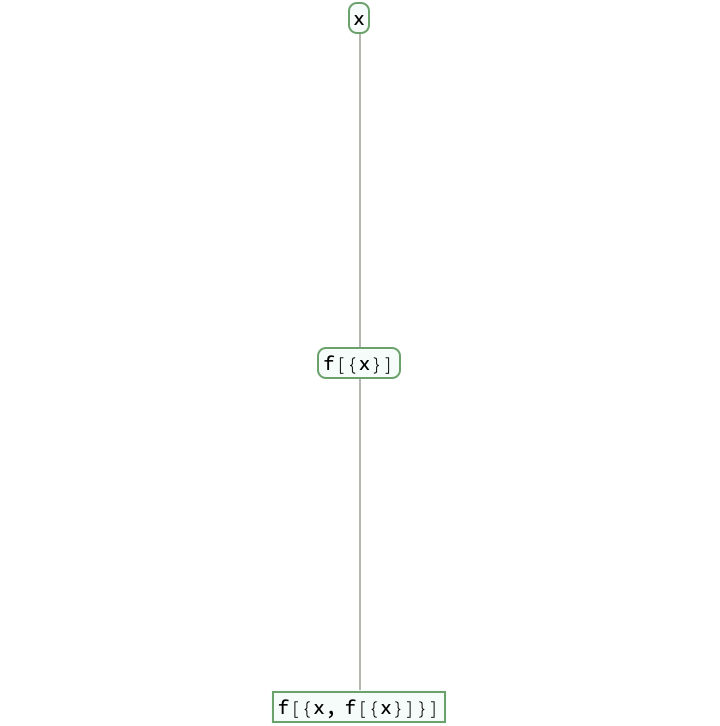Style the tree:

In[3]:=
ResourceFunction[ "AncestralNestTree", ResourceSystemBase -> "https://www.wolframcloud.com/obj/resourcesystem/api/1.0"][{f[#], g[#]} &, x, 2, BaseStyle -> LightBlue]
Out[3]=

Applications (3) 

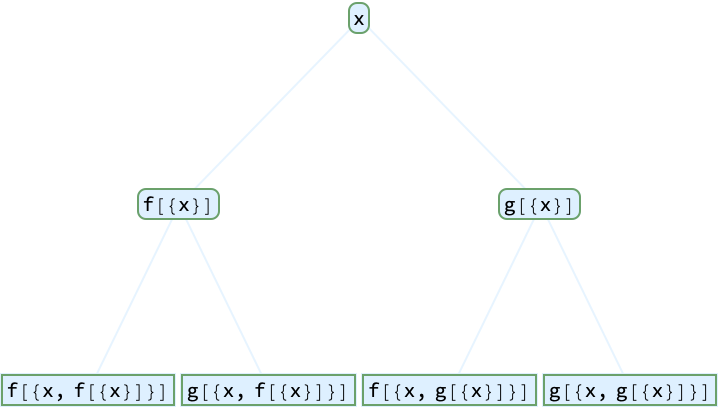Store all permutations of {a,b,c,d} as paths from the root id to leaves:

In[4]:=
permTree = ResourceFunction[ "AncestralNestTree", ResourceSystemBase -> "https://www.wolframcloud.com/obj/resourcesystem/api/1.0"][Complement[{"a", "b", "c", "d"}, #] &, Tree["id", None], Infinity]
Out[4]=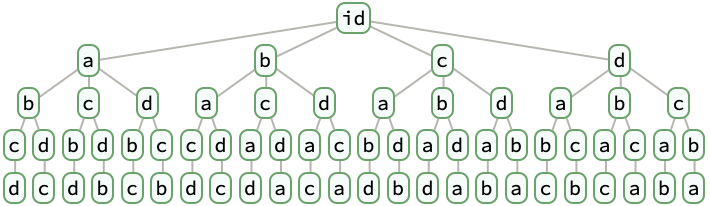

Associate each of a,b,c,d with square matrices, and id with the identity matrix:

In[5]:=
matrixAssociation = Append[AssociationMap[ RandomInteger[{-5, 5}, {2, 2}] &, {"a", "b", "c", "d"}], "id" -> IdentityMatrix[2]]
Out[5]=

Find all matrix products involving each matrix at most once without having to repeat subcomputations or store more than five matrix products at a time:

In[6]:=
ResourceFunction["AncestralTreeScan"][ Function[{productList, matKey}, {matKey, If[productList == {}, matrixAssociation[matKey], productList[[-1, 2]] . matrixAssociation[matKey]]} ], Function[{productList}, Print[If[Length@productList == 1, productList[[1, 1]], Dot @@ Rest@productList[[All, 1]]] == productList[[-1, 2]]] ], permTree ]

Properties and Relations (1) 

AncestralNestTree[f@*Last,args] is equivalent to NestTree[f,args] in most cases:

In[7]:=
{ResourceFunction[ "AncestralNestTree", ResourceSystemBase -> "https://www.wolframcloud.com/obj/resourcesystem/api/1.0"][Rest@*Most@*Divisors@*Last, \!\(\* GraphicsBox[ NamespaceBox["Trees", DynamicModuleBox[{Typeset`tree = HoldComplete[ Tree[Null, { Tree[4, None], Tree[6, None]}]]}, NamespaceBox[{ {Hue[0.6, 0.7, 0.5], Opacity[0.7], Arrowheads[Medium], {RGBColor[0.6, 0.5882352941176471, 0.5529411764705883], AbsoluteThickness[1], LineBox[{{0.4472135954999579, 0.8929961074943159}, {0., 0.}}]}, {RGBColor[0.6, 0.5882352941176471, 0.5529411764705883], AbsoluteThickness[1], LineBox[{{0.4472135954999579, 0.8929961074943159}, { 0.8944271909999159, 0.}}]}}, {Hue[0.6, 0.2, 0.8], EdgeForm[{GrayLevel[0], Opacity[0.7]}], TagBox[InsetBox[ FrameBox["", Background->Directive[ RGBColor[0.9607843137254902, 0.9882352941176471, 0.9764705882352941]], BaseStyle->GrayLevel[0], FrameStyle->Directive[ RGBColor[0.4196078431372549, 0.6313725490196078, 0.4196078431372549], AbsoluteThickness[1], Opacity[1]], ImageSize->{1, 1}, RoundingRadius->4, StripOnInput->False], {0.4472135954999579, 0.8929961074943159}], "DynamicName", BoxID -> "VertexID$1"], TagBox[InsetBox[ FrameBox["4", Background->Directive[ RGBColor[0.9607843137254902, 0.9882352941176471, 0.9764705882352941]], BaseStyle->GrayLevel[0], FrameMargins->{{2, 2}, {1, 1}}, FrameStyle->Directive[ RGBColor[0.4196078431372549, 0.6313725490196078, 0.4196078431372549], AbsoluteThickness[1], Opacity[1]], ImageSize->Automatic, RoundingRadius->0, StripOnInput->False], {0., 0.}], "DynamicName", BoxID -> "VertexID$2"], TagBox[InsetBox[ FrameBox["6", Background->Directive[ RGBColor[0.9607843137254902, 0.9882352941176471, 0.9764705882352941]], BaseStyle->GrayLevel[0], FrameMargins->{{2, 2}, {1, 1}}, FrameStyle->Directive[ RGBColor[0.4196078431372549, 0.6313725490196078, 0.4196078431372549], AbsoluteThickness[1], Opacity[1]], ImageSize->Automatic, RoundingRadius->0, StripOnInput->False], {0.8944271909999159, 0.}], "DynamicName", BoxID -> "VertexID$3"]}}]]], AlignmentPoint->Center, Axes->False, AxesLabel->None, AxesOrigin->Automatic, AxesStyle->{}, Background->None, BaseStyle->{}, BaselinePosition->Automatic, ContentSelectable->Automatic, DefaultBaseStyle->"TreeGraphics", DisplayFunction->Identity, Epilog->{}, FormatType->StandardForm, Frame->False, FrameLabel->None, FrameStyle->{}, FrameTicks->None, FrameTicksStyle->{}, GridLines->None, GridLinesStyle->{}, ImageMargins->0., ImagePadding->All, ImageSize->{35.55889892578125, Automatic}, LabelStyle->{}, PlotLabel->None, PlotRange->All, PlotRangeClipping->False, PlotRangePadding->Automatic, PlotRegion->Automatic, Prolog->{}, RotateLabel->True, Ticks->Automatic, TicksStyle->{}]\), 1, FactorInteger], NestTree[Rest@*Most@*Divisors, \!\(\* GraphicsBox[ NamespaceBox["Trees", DynamicModuleBox[{Typeset`tree = HoldComplete[ Tree[Null, { Tree[4, None], Tree[6, None]}]]}, NamespaceBox[{ {Hue[0.6, 0.7, 0.5], Opacity[0.7], Arrowheads[Medium], {RGBColor[0.6, 0.5882352941176471, 0.5529411764705883], AbsoluteThickness[1], LineBox[{{0.4472135954999579, 0.8929961074943159}, {0., 0.}}]}, {RGBColor[0.6, 0.5882352941176471, 0.5529411764705883], AbsoluteThickness[1], LineBox[{{0.4472135954999579, 0.8929961074943159}, { 0.8944271909999159, 0.}}]}}, {Hue[0.6, 0.2, 0.8], EdgeForm[{GrayLevel[0], Opacity[0.7]}], TagBox[InsetBox[ FrameBox["", Background->Directive[ RGBColor[0.9607843137254902, 0.9882352941176471, 0.9764705882352941]], BaseStyle->GrayLevel[0], FrameStyle->Directive[ RGBColor[0.4196078431372549, 0.6313725490196078, 0.4196078431372549], AbsoluteThickness[1], Opacity[1]], ImageSize->{1, 1}, RoundingRadius->4, StripOnInput->False], {0.4472135954999579, 0.8929961074943159}], "DynamicName", BoxID -> "VertexID$1"], TagBox[InsetBox[ FrameBox["4", Background->Directive[ RGBColor[0.9607843137254902, 0.9882352941176471, 0.9764705882352941]], BaseStyle->GrayLevel[0], FrameMargins->{{2, 2}, {1, 1}}, FrameStyle->Directive[ RGBColor[0.4196078431372549, 0.6313725490196078, 0.4196078431372549], AbsoluteThickness[1], Opacity[1]], ImageSize->Automatic, RoundingRadius->0, StripOnInput->False], {0., 0.}], "DynamicName", BoxID -> "VertexID$2"], TagBox[InsetBox[ FrameBox["6", Background->Directive[ RGBColor[0.9607843137254902, 0.9882352941176471, 0.9764705882352941]], BaseStyle->GrayLevel[0], FrameMargins->{{2, 2}, {1, 1}}, FrameStyle->Directive[ RGBColor[0.4196078431372549, 0.6313725490196078, 0.4196078431372549], AbsoluteThickness[1], Opacity[1]], ImageSize->Automatic, RoundingRadius->0, StripOnInput->False], {0.8944271909999159, 0.}], "DynamicName", BoxID -> "VertexID$3"]}}]]], AlignmentPoint->Center, Axes->False, AxesLabel->None, AxesOrigin->Automatic, AxesStyle->{}, Background->None, BaseStyle->{}, BaselinePosition->Automatic, ContentSelectable->Automatic, DefaultBaseStyle->"TreeGraphics", DisplayFunction->Identity, Epilog->{}, FormatType->StandardForm, Frame->False, FrameLabel->None, FrameStyle->{}, FrameTicks->None, FrameTicksStyle->{}, GridLines->None, GridLinesStyle->{}, ImageMargins->0., ImagePadding->All, ImageSize->{35.55889892578125, Automatic}, LabelStyle->{}, PlotLabel->None, PlotRange->All, PlotRangeClipping->False, PlotRangePadding->Automatic, PlotRegion->Automatic, Prolog->{}, RotateLabel->True, Ticks->Automatic, TicksStyle->{}]\), 1, FactorInteger]}
Out[7]=

Publisher

Daniel McDonald

Requirements

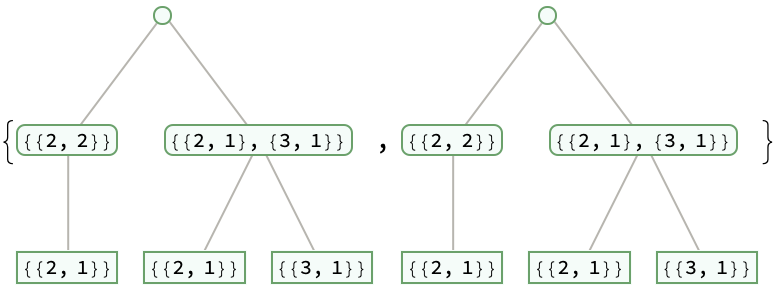Wolfram Language 13.0 (December 2021) or above

Version History

  • 1.1.0 – 10 September 2025
  • 1.0.0 – 20 November 2024

Related Resources

License Information