Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Construct an alternating tree graph
ResourceFunction["AlternatingTreeGraph"][n] generates an alternating tree graph from a path graph with n vertices. |
Make an alternating tree graph from the path graph with 10 vertices:
| In[1]:= |
| Out[1]= |  |
Create a large alternating tree graph:
| In[2]:= |
| Out[2]= |
All graph layouts can be selected:
| In[3]:= | ![Table[Labeled[
ResourceFunction["AlternatingTreeGraph"][10, GraphLayout -> embedding], embedding], {embedding, {"BipartiteEmbedding", "CircularEmbedding", "CircularMultipartiteEmbedding", "DiscreteSpiralEmbedding", "GridEmbedding", "LinearEmbedding", "MultipartiteEmbedding", "StarEmbedding", "BalloonEmbedding", "RadialEmbedding", "LayeredEmbedding", "GravityEmbedding", "HighDimensionalEmbedding",
"SpectralEmbedding", "SphericalEmbedding", "SpringElectricalEmbedding", "SpringEmbedding", "TutteEmbedding"}}]](https://www.wolframcloud.com/obj/resourcesystem/images/07f/07f7294a-d16e-4210-a09f-edbc35ca41f3/126f897c29930408.png) |
| Out[3]= | 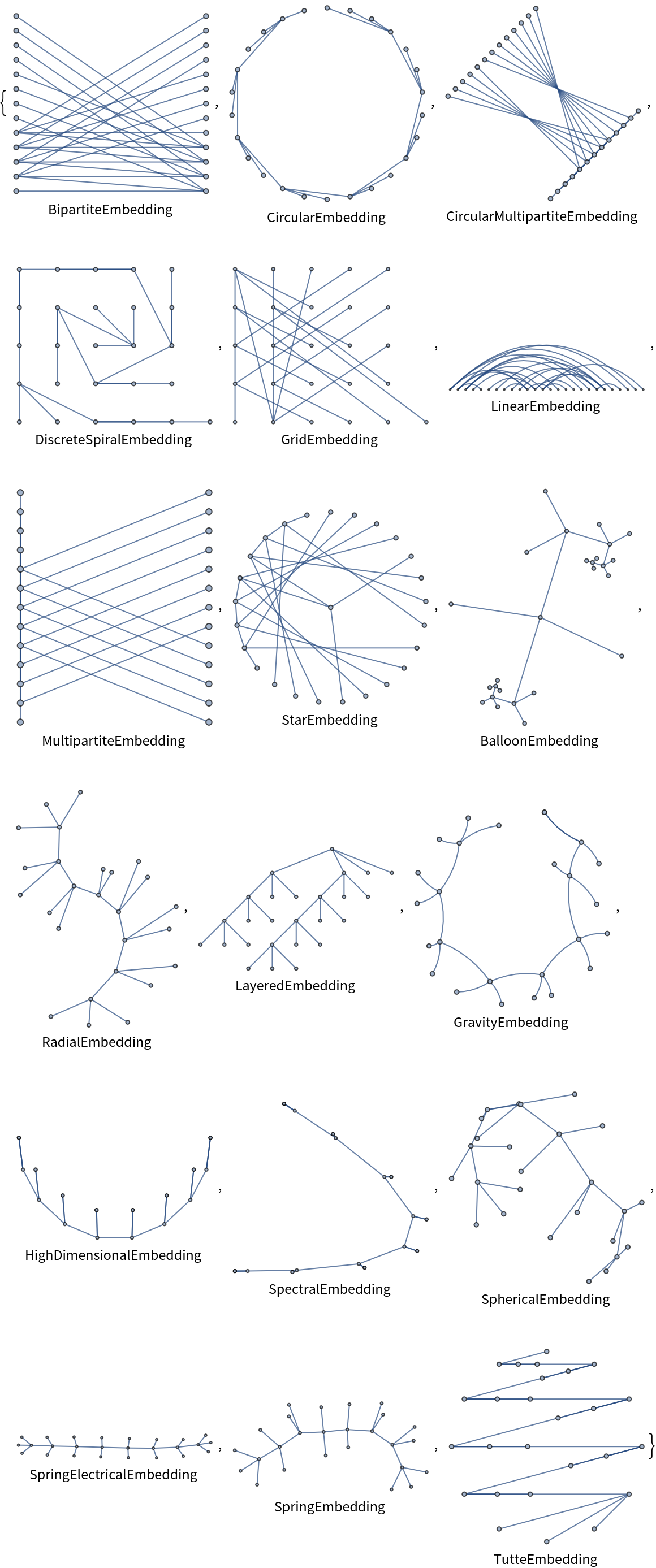 |
Try SpringEmbedding if SpringElectricalEmbedding does not work well:
| In[4]:= |
| Out[4]= |
| In[5]:= |
| Out[5]= |  |
Find the graph center and graph periphery:
| In[6]:= |
| Out[6]= |  |
| In[7]:= |
| Out[7]= |  |
Use FindSequenceFunction to find a pattern in the order and size of the graph:
| In[8]:= |
| Out[8]= | 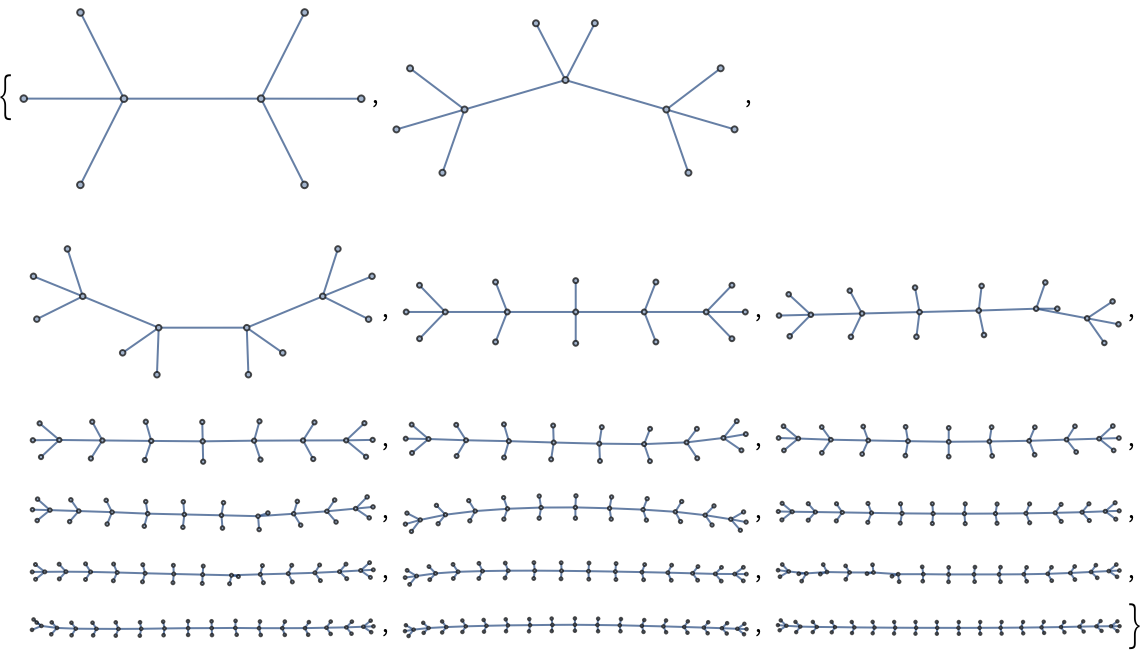 |
| In[9]:= |
| Out[9]= |
| In[10]:= |
| Out[10]= |
Predict the size of a 2980 length alternating tree:
| In[11]:= |
| Out[11]= | 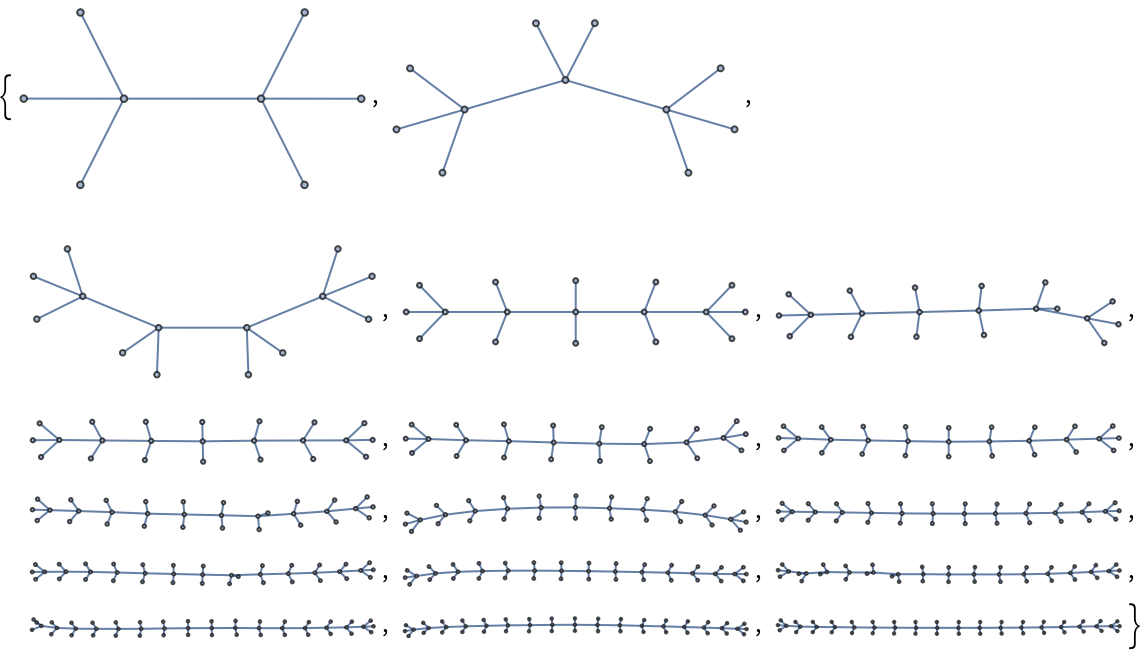 |
| In[12]:= |
| Out[12]= |
| In[13]:= |
| Out[13]= |
Wolfram Language 12.3 (May 2021) or above
This work is licensed under a Creative Commons Attribution 4.0 International License