Function Repository Resource:

AlphaBetaSearch

Source Notebook

Find solutions to perfectly played combinatorial games

Contributed by: Brad Klee and Andrea Li

ResourceFunction["AlphaBetaSearch"][iterator,init,player,result]

returns a partial game graph for sufficiently determining the winner of a two player game.

ResourceFunction["AlphaBetaSearch"][iterator,init,player,result,heuristic]

allows ordered searching through the sort function heuristic.

ResourceFunction["AlphaBetaSearch"][iterator,init,player,result,heuristic,goals]

allows for games with more than two players by setting goals.

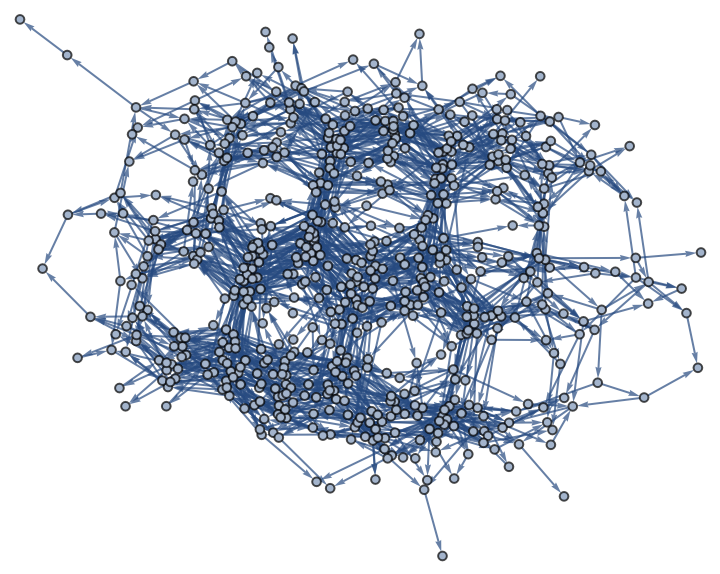
Details

Function iterator takes a game state as input, and outputs all valid next states.

Expression init is the unique starting configuration of the game.

Function player takes a state as input and returns the player whose turn it is. The default players are

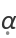
and

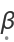
The function result takes a terminal game state as input and returns a value for the position. The default values are assumed to be 1 when

wins, -1 when

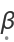
wins and 0 for a draw.

Function heuristic can be used to sort potential next game states: next= heuristic[iterator[state]]. Most useful heuristics will be of the form heuristic=Function[SortBy[#,…]]. For statistical testing heuristic=RandomSample can also be useful.

Association goals links player symbols to game state values and describes how each player chooses a best next state. By default, player

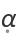
chooses by Max, and player

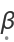
chooses by Min. The form for each item of goals is player → 〈| "Win" → val, "Choose" → fun |〉, which assumes that function fun when applied to a list of game state values will choose val if it occurs in the list.

AlphaBetaSearch accepts two options Method and PerformanceGoal.

Default Method "Loop" has extra cancellations, but alternative method "Recursive" is competitively performant.

Setting PerformanceGoal to "Quality" certifies the result with a post-check of the closure conditions.

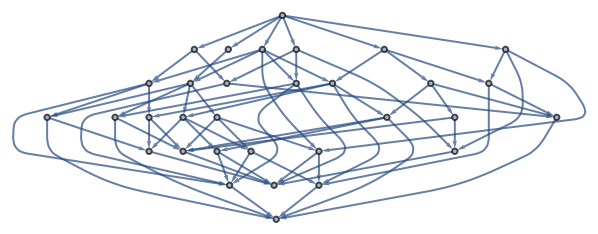
The result of ResourceFunction["AlphaBetaSearch"] is always a subgraph of ResourceFunction["FixedPointGraph"][iterator, {init}].

The result of ResourceFunction["AlphaBetaSearch"] always satisfies a closure condition as shown in Properties and Relations.

A valid result is only guaranteed for a directed acyclic iterator. If iterator finds loops in the game graph, the algorithm can not be expected to succeed.

Examples

Basic Examples (2)

Solve a two-player nim game with three heaps:

In[1]:=

$gnim = ResourceFunction["AlphaBetaSearch"][Function[state, Thread[{ Catenate[ Map[Tuples[ MapAt[Range[0, First[#] - 1]& , Map[List, First[state]], #]]& , Range[ Length[ First[state]]]]], <|\[FormalAlpha] -> \[FormalBeta], \[FormalBeta] -> \[FormalAlpha]|>[ Last[state]]}]], {{1, 2, 3}, \[FormalAlpha]}, Last[#] &, Association[\[FormalAlpha] -> -1, \[FormalBeta] -> 1][Last[#]] &]$

Out[1]=

Use the "nim-sum equals zero" heuristic to obtain a smaller solution:

In[2]:=

$gnim0 = ResourceFunction["AlphaBetaSearch"][Function[state, Thread[{ Catenate[ Map[Tuples[ MapAt[Range[0, First[#] - 1]& , Map[List, First[state]], #]]& , Range[ Length[ First[state]]]]], <|\[FormalAlpha] -> \[FormalBeta], \[FormalBeta] -> \[FormalAlpha]|>[ Last[state]]}]], {{1, 2, 3}, \[FormalAlpha]}, Last[#] &, Association[\[FormalAlpha] -> -1, \[FormalBeta] -> 1][Last[#]] &, Function[SortBy[#, BitXor @@ First[#, {}] &]]]$

Out[2]=

Highlight solutions on the entire game graph:

In[3]:=

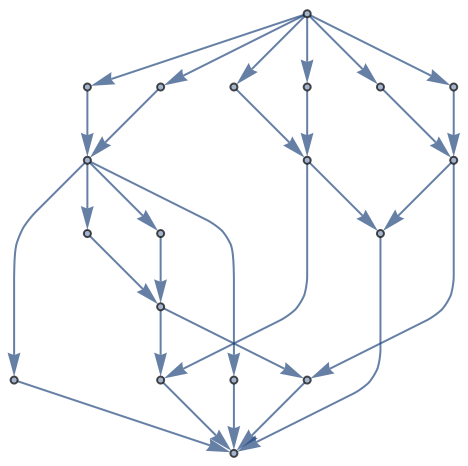
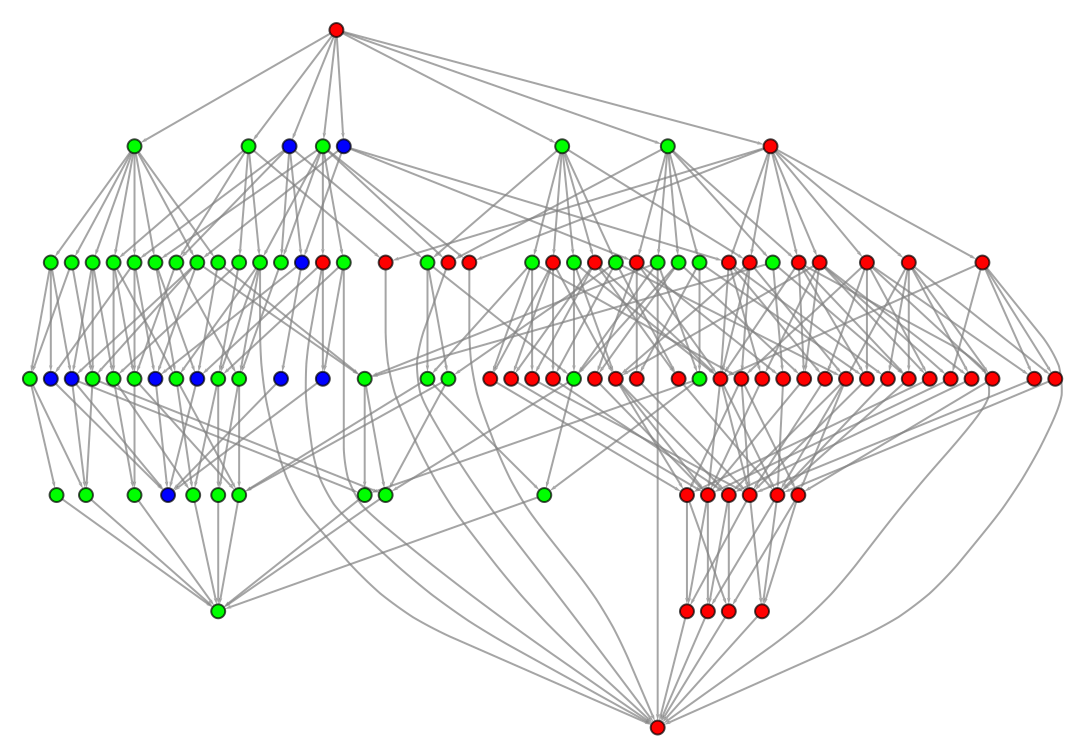
$HighlightGraph[ResourceFunction["FixedPointGraph"][ Function[state, Thread[{ Catenate[ Map[Tuples[ MapAt[Range[0, First[#] - 1]& , Map[List, First[state]], #]]& , Range[ Length[ First[state]]]]], <|\[FormalAlpha] -> \[FormalBeta], \[FormalBeta] -> \[FormalAlpha]|>[ Last[state]]}]], {{{1, 2, 3}, \[FormalAlpha]}}, GraphLayout -> "LayeredDigraphEmbedding", EdgeStyle -> Lighter@Gray, AspectRatio -> 2/3], {Style[gnim, Lighter@Orange], Style[gnim0, Red]}]$

Out[3]=

Check that both solutions predict the same winner:

In[4]:=

$AnnotationValue[{#, {{1, 2, 3}, \[FormalAlpha]}}, VertexWeight] & /@ {gnim, gnim0}$

Out[4]=

Find a solution to the independence game on a small RandomGraph:

In[5]:=

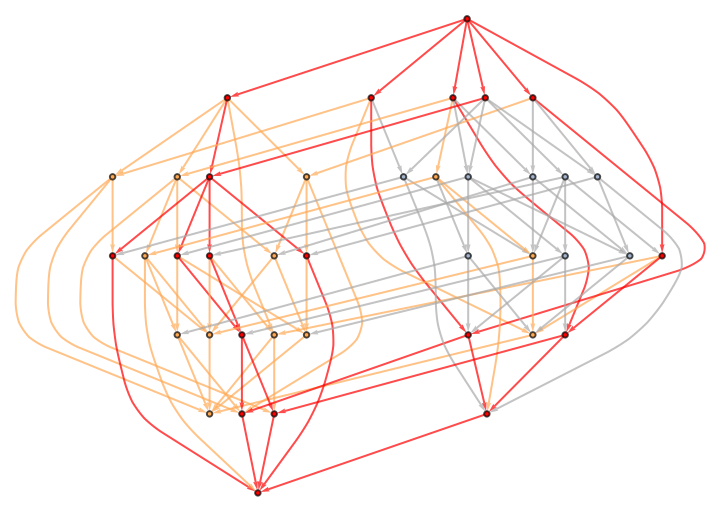
$gind = ResourceFunction["AlphaBetaSearch"][Function[state, Union[ Thread[{ Map[VertexDelete[ First[state], VertexOutComponent[ First[state], #, 1]]& , VertexList[ First[state]]], <|\[FormalAlpha] -> \[FormalBeta], \[FormalBeta] -> \[FormalAlpha]|>[ Last[state]]}]]], SeedRandom[234]; {RandomGraph[{10, 20}], \[FormalAlpha]}, Last[#] &, Association[\[FormalAlpha] -> -1, \[FormalBeta] -> 1][Last[#]] &]$

Out[5]=

Decorate the graph to see which branch would follow from an imperfect choice:

In[6]:=

$Graph[gind, VertexStyle -> Thread[VertexList[gind] -> Lookup[Association[\[FormalAlpha] -> Red, \[FormalBeta] -> Blue], AnnotationValue[gind, VertexWeight]]], EdgeStyle -> Gray]$

Out[6]=

Scope (3)

Define win conditions and choice functions for a three-player game:

In[7]:=

$$ThreePlayers = Association[MapIndexed[Function[{var, ind}, var -> Association[ "Choose" -> Function[opts, SelectFirst[#, MemberQ[opts, #] &]] , "Win" -> ind[[1]]] &[ RotateLeft[{1, 2, 3}, ind[[1]] - 1]]], {\[FormalAlpha], \[FormalBeta], \[FormalGamma]}]]$

Out[7]=

One solution for a three-player vertex deletion game on a small RandomGraph:

In[8]:=

$gind = ResourceFunction["AlphaBetaSearch"][Function[state, Union[ Thread[{ Map[VertexDelete[ First[state], VertexOutComponent[ First[state], #, 1]]& , VertexList[ First[state]]], <|\[FormalAlpha] -> \[FormalBeta], \[FormalBeta] -> \[FormalGamma], \[FormalGamma] -> \[FormalAlpha]|>[ Last[state]]}]]], SeedRandom[2345]; {RandomGraph[{13, 25}], \[FormalAlpha]}, Last[#] &, Association[\[FormalAlpha] -> 1, \[FormalBeta] -> 2, \[FormalGamma] -> 3][Last[#]] &, Identity, $ThreePlayers ]$

Out[8]=

Decorate the graph to see who wins and how:

In[9]:=

$Graph[gind, VertexStyle -> Thread[VertexList[gind] -> Lookup[Association[\[FormalAlpha] -> Red, \[FormalBeta] -> Blue, \[FormalGamma] -> Green], AnnotationValue[gind, VertexWeight]]], EdgeStyle -> Gray, AspectRatio -> 2/3, VertexSize -> 2/3, GraphLayout -> "LayeredDigraphEmbedding"]$

Out[9]=

Options (2)

Obtain a validated result for a simple arithmetic game:

In[10]:=

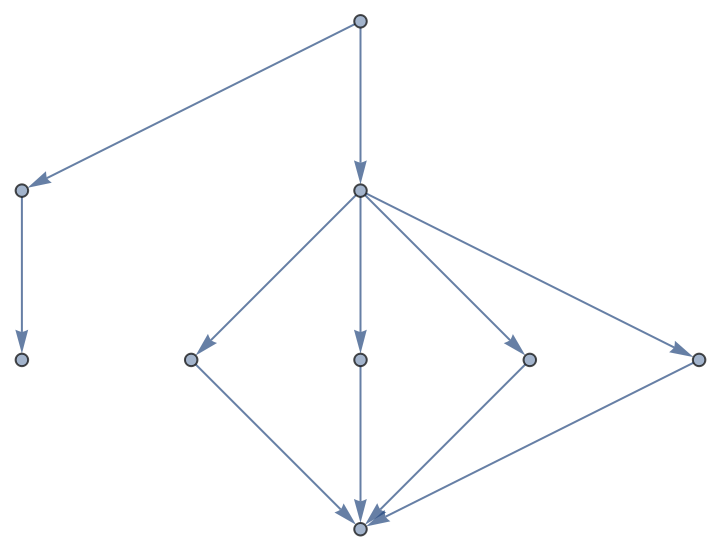
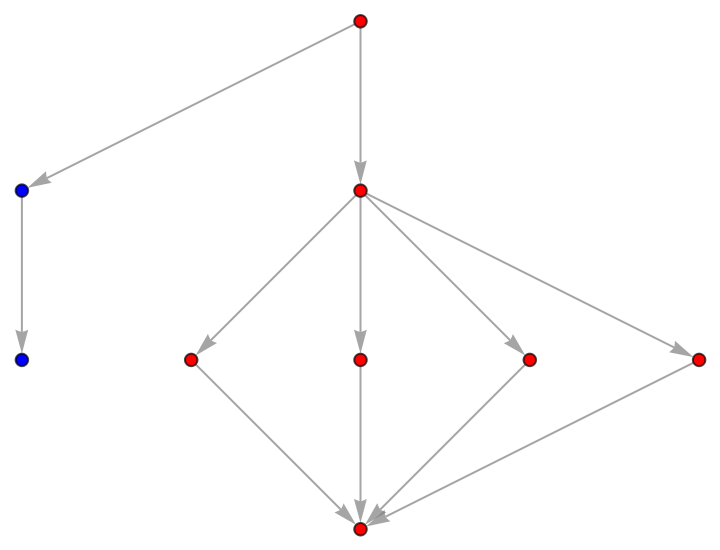
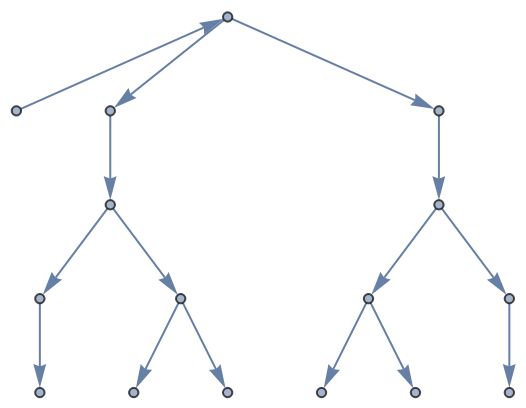
$ResourceFunction["AlphaBetaSearch"][ If[Depth[#] < 6, {f[#, 2], f[2, #]}, {}] &, 1, Function[If[OddQ[Depth[#]], \[FormalAlpha], \[FormalBeta]]], Function[Switch[Head[# /. f -> Divide], Rational, 1, Integer, -1]], PerformanceGoal -> "Quality"]$

Out[10]=

Obtain solutions for a nim game using two different methods:

In[11]:=

$sols = ResourceFunction["AlphaBetaSearch"][Function[state, Thread[{ Catenate[ Map[Tuples[ MapAt[Range[0, First[#] - 1]& , Map[List, First[state]], #]]& , Range[ Length[ First[state]]]]], <|\[FormalAlpha] -> \[FormalBeta], \[FormalBeta] -> \[FormalAlpha]|>[ Last[state]]}]], {{1, 2, 2}, \[FormalAlpha]}, Last[#] &, Association[\[FormalAlpha] -> -1, \[FormalBeta] -> 1][Last[#]] &, Method -> #] & /@ {"Loop", "Recursive"}$

Out[11]=

The solutions are different:

In[12]:=

Out[12]=

But both solutions predict the same winner by perfect play:

In[13]:=

$AnnotationValue[{#, {{1, 2, 2}, \[FormalAlpha]}}, VertexWeight] & /@ sols$

Out[13]=

Properties and Relations (5)

Compute a solution:

In[14]:=

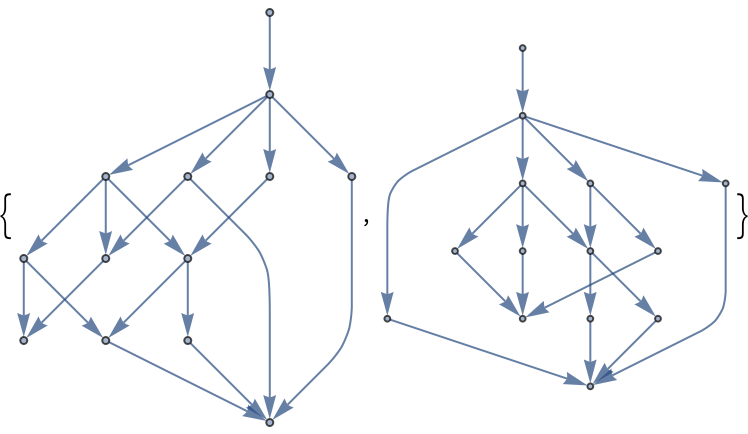
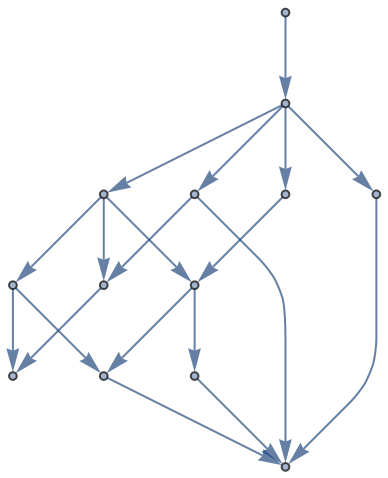
$g1 = ResourceFunction["AlphaBetaSearch"][Function[state, Thread[{ Catenate[ Map[Tuples[ MapAt[Range[0, First[#] - 1]& , Map[List, First[state]], #]]& , Range[ Length[ First[state]]]]], <|\[FormalAlpha] -> \[FormalBeta], \[FormalBeta] -> \[FormalAlpha]|>[ Last[state]]}]], {{1, 2, 2}, \[FormalAlpha]}, Last[#] &, Association[\[FormalAlpha] -> -1, \[FormalBeta] -> 1][Last[#]] &]$

Out[14]=

Expand one extra layer of vertices around the solution:

In[15]:=

$g2 = HighlightGraph[NestGraph[Function[state, Thread[{ Catenate[ Map[Tuples[ MapAt[Range[0, First[#] - 1]& , Map[List, First[state]], #]]& , Range[ Length[ First[state]]]]], <|\[FormalAlpha] -> \[FormalBeta], \[FormalBeta] -> \[FormalAlpha]|>[ Last[state]]}]], g1, 1], g1]$

Out[15]=

Losing positions must not have missing next steps:

In[16]:=

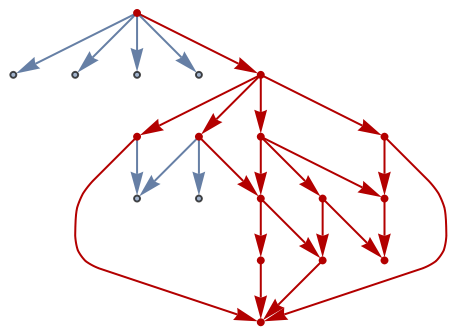
AllTrue[Select[VertexList[g1],
UnsameQ[Last[#], AnnotationValue[{g1, #}, VertexWeight]] &],
SameQ[VertexOutDegree[g1, #], VertexOutDegree[g2, #]] &]

Out[16]=

Missing next steps must branch from winning positions:

In[17]:=

AllTrue[Union[Catenate[VertexInComponent[g2, #, {1}
] & /@ Complement[VertexList[g2], VertexList[g1]]]],
SameQ[Last[#], AnnotationValue[{g1, #}, VertexWeight]] &]

Out[17]=

These checks can be computed automatically:

In[18]:=

$! FailureQ[ResourceFunction["AlphaBetaSearch"][Function[state, Thread[{ Catenate[ Map[Tuples[ MapAt[Range[0, First[#] - 1]& , Map[List, First[state]], #]]& , Range[ Length[ First[state]]]]], <|\[FormalAlpha] -> \[FormalBeta], \[FormalBeta] -> \[FormalAlpha]|>[ Last[state]]}]], {{1, 2, 2}, \[FormalAlpha]}, Last[#] &, Association[\[FormalAlpha] -> -1, \[FormalBeta] -> 1][Last[#]] &, PerformanceGoal -> "Quality"]]$

Out[18]=

Neat Examples (2)

A solution to the game tic-tac-toe:

In[19]:=

$gttt = ResourceFunction["AlphaBetaSearch"][Function[state, Module[{sign, res, inds, winner, wins}, wins = {{{1, 1}, {2, 1}, {3, 1}}, {{1, 2}, {2, 2}, {3, 2}}, {{1, 3}, {2, 3}, {3, 3}}, {{1, 1}, {1, 2}, {1, 3}}, {{2, 1}, {2, 2}, {2, 3}}, {{3, 1}, {3, 2}, {3, 3}}, {{1, 3}, {2, 2}, {3, 1}}, {{1, 1}, {2, 2}, {3, 3}}}; sign = Switch[ If[Count[state, 1, 2] === Count[ state, -1, 2], \[FormalAlpha], \[FormalBeta]], \[FormalAlpha], 1, \[FormalBeta], -1]; If[ Not[ TrueQ[inds = SelectFirst[wins, Function[inds, And[ Apply[SameQ, Map[Part[state, Apply[Sequence, #]]& , inds]], (winner = Part[state, Apply[Sequence, Part[inds, 1]]]) =!= 0]], True]; If[ TrueQ[inds], If[ AllTrue[wins, Function[inds, SubsetQ[ Map[Part[state, Apply[Sequence, #]]& , inds], {1, -1}]]], 0, True], winner]]], {}, res = Map[ReplacePart[state, # -> sign]& , Position[state, 0]]; res = Union[ Map[ Composition[First, Sort, ResourceFunction["ArrayRotations"]], res]]]]], ConstantArray[0, {3, 3}], Function[state, If[Count[state, 1, 2] === Count[ state, -1, 2], \[FormalAlpha], \[FormalBeta]]], Function[state, Module[{inds, winner, wins}, wins = {{{1, 1}, {2, 1}, {3, 1}}, {{1, 2}, {2, 2}, {3, 2}}, {{1, 3}, {2, 3}, {3, 3}}, {{1, 1}, {1, 2}, {1, 3}}, {{2, 1}, {2, 2}, {2, 3}}, {{3, 1}, {3, 2}, {3, 3}}, {{1, 3}, {2, 2}, {3, 1}}, {{1, 1}, {2, 2}, {3, 3}}}; inds = SelectFirst[wins, Function[inds, And[ Apply[SameQ, Map[Part[state, Apply[Sequence, #]]& , inds]], (winner = Part[state, Apply[Sequence, Part[inds, 1]]]) =!= 0]], True]; If[ TrueQ[inds], If[ AllTrue[wins, Function[inds, SubsetQ[ Map[Part[state, Apply[Sequence, #]]& , inds], {1, -1}]]], 0, True], winner]]]]$

Out[19]=

Check that perfect play leads to a draw:

In[20]:=

Out[20]=

Publisher

Brad Klee

Requirements

Wolfram Language 13.0 (December 2021) or above

Version History

1.0.0 – 24 May 2024

Related Resources

Author Notes

Andrea Li contributed recursive method. Loop method and final draft were written and compiled by Bradley Klee.

License Information

This work is licensed under a Creative Commons Attribution 4.0 International License

Wolfram Function Repository

AlphaBetaSearch

Details