Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 AlgebraicSubstitutionTiling

Source Notebook

Return a substitution tiling

Contributed by: Ed Pegg Jr

ResourceFunction["AlgebraicSubstitutionTiling"][tiling,steps]

with the given tiling system specified by tiling, return the state after steps substitutions.

Details and Options

A third argument can specify alternate starting states or numeric approximations (faster).
The possible named values for tiling are: "PinwheelTiling", "DominoTiling", "TrominoTiling", "LTetrominoTiling", "PPentominoTiling", "Tritan3Tiling", "Tritan4Tiling", "TriangleDuo", "WaltonChair", "SqrtTwo", "SqrtTwo2", "Drafter3", "Drafter4", "HalfHex", "QuarterHex", "Kite", "SphinxTiling", "LimhexTiling", "AmmannA4Tiling", "AmmannChairTiling", "KitesandDartsTiling", "PenroseTriangleTiling", "PenroseRhombTiling", "BinaryTiling", "SqrtPhi", "SqrtPsi", "SqrtRho", "SqrtRho2", "SqrtRho3", "SqrtRho4", "TribonacciChordQuadrangle", "SqrtChi", "SqrtChi2", "SqrtChi3", "SqrtChi4", "QuarticPinwheel".

Examples

Basic Examples (3) 

Show a starting kite after two substitution steps with the Penrose kites and darts tiling system:

In[1]:=
ResourceFunction["AlgebraicSubstitutionTiling"]["KitesandDarts", 2]
Out[1]=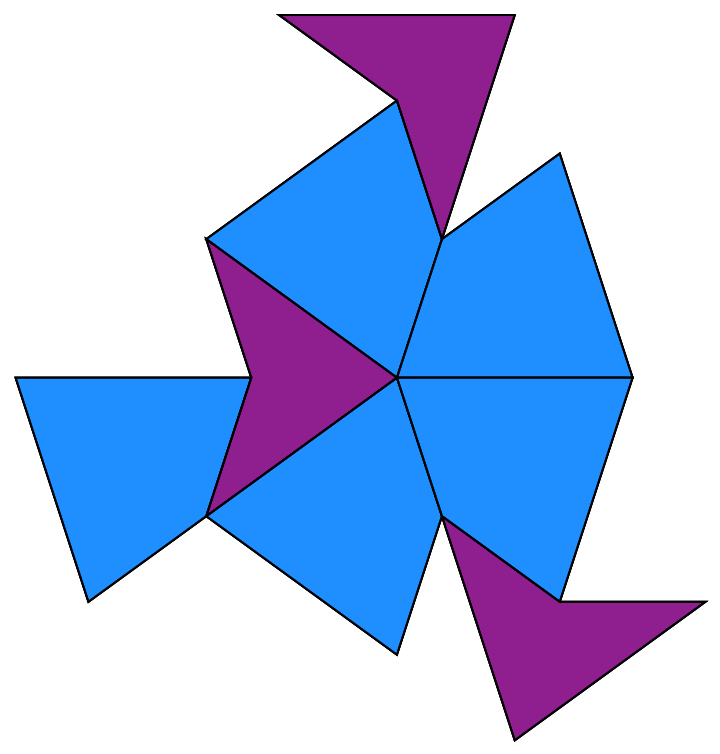

With steps=0, the substitution tiling itself is shown, as with the Penrose kites and darts tiling system:

In[2]:=
ResourceFunction["AlgebraicSubstitutionTiling"]["KitesandDarts", 0]
Out[2]=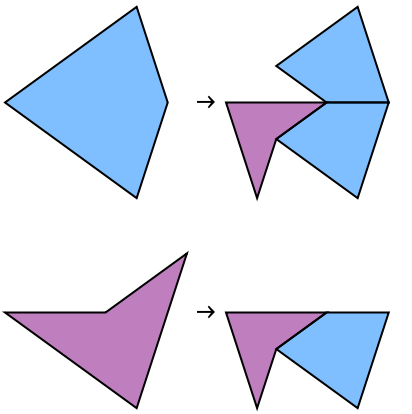

Show the pinwheel tiling with an alternate start:

In[3]:=
ResourceFunction[ "AlgebraicSubstitutionTiling"]["Pinwheel", 3, {"N", "Start" -> {{{0, 0}, {0, 1}, {2, 1}}, {{2, 1}, {2, 0}, {0, 0}}}}]
Out[3]=

Scope (1) 

Show the numerically approximated second step of all name-supported tilings:

In[4]:=
Column[{Text@#, ResourceFunction["AlgebraicSubstitutionTiling"][#, 2, {"N"}]}, Alignment -> Center] & /@ {"Pinwheel", "Domino", "Tromino", "LTetromino", "PPentomino", "Tritan4", "Drafter3", "Drafter4", "HalfHex", "QuarterHex", "Sphinx", "Limhex", "Tritan3", "Kite", "Equithirds", "TriangleDuo", "AmmannChair", "AmmannPhiChair", "WaltonChair", "AmmannA4", "KitesandDarts", "RobinsonTriangle", "PenroseRhomb", "Binary", "PsiQuad", "RhoQuad", "TwoTriangle", "TribonacciChordQuadrangle", "PsiChordQuadrangle", "RhoChordQuadrangle", "SqrtTwo", "SqrtPhi", "SqrtPsi", "SqrtRho", "SqrtChi", "QuarticPinwheel"}
Out[4]=

Options (2) 

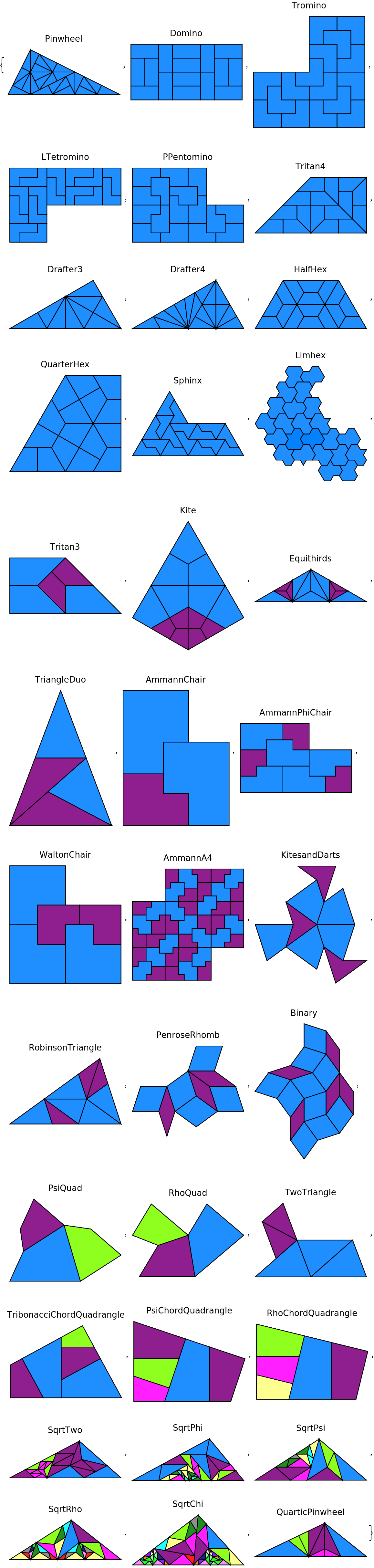The Penrose kites and darts tiling system with the root, algebraic points in terms of that root, polygon substitutions and polygon types:

In[5]:=
ResourceFunction["AlgebraicSubstitutionTiling"][{ GoldenRatio, {{{0, 0}, {0, 0}}, {{1/4, 0}, {7/4, -1}}, {{2, -1}, {0, 0}}, {{1/4, 0}, {-(7/4), 1}}, {{5, -3}, {0, 0}}, {{5/4, -(3/4)}, {47/ 4, -(29/4)}}, {{5/4, -(3/4)}, {-(47/4), 29/4}}, {{13/ 4, -2}, {-(7/4), 1}}, {{5/2, -(5/4)}, {9/2, -(11/4)}}}, {{1, 2, 3, 4} -> {{2, 3, 5, 6}, {4, 7, 5, 3}, {1, 5, 7, 8}}, {4, 1, 5, 9} -> {{4, 7, 5, 3}, {1, 5, 7, 8}}}, {{1, 1, 2}, {1, 2}}}, 2]
Out[5]=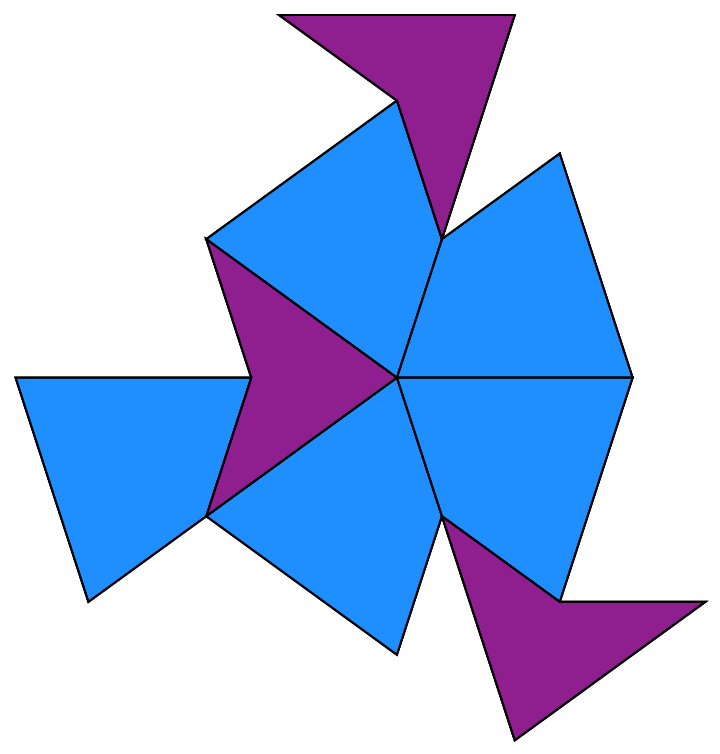

A chord tiling with a plastic constant (ρ) root, algebraic points in terms of ρ, polygon substitutions and polygon types:

In[6]:=
ResourceFunction["AlgebraicSubstitutionTiling"][{ Root[-1 - #1 + #1^3 &, 1], {{{-1, 0, 0}, {-2, -4, -3}}, {{0, 0, 0}, {-2, -4, -3}}, {{1, 2, 1}, {-2, -4, -3}}, {{1, 4, 4}, {-2, -4, -3}}, {{7, 13, 12}, {-2, -4, -3}}, {{13, 22, 17}, {-2, -4, -3}}, {{-(48/49), -(52/49), -(37/49)}, {-(1/49), 3/ 49, -(12/49)}}, {{0, 0, 0}, {0, 0, 0}}, {{-(11/49), 33/49, 15/ 49}, {11/49, 16/49, -(15/49)}}, {{1, 4, 4}, {0, 1, 0}}, {{208/49, 356/49, 340/49}, {-(12/49), 36/49, 52/49}}, {{13, 22, 17}, {1, 2, 2}}}, {{12, 6, 1, 7} -> {{8, 7, 1, 2}, {3, 2, 8, 9}, {8, 7, 1, 2} + 2, {3, 2, 8, 9} + 2, {8, 7, 1, 2} + 4}}, {{1, 1, 1, 1, 1}}}, 3, {"N"}]
Out[6]=

Applications (1) 

Show polygons of every step as a layered graphic:

In[7]:=
Graphics[ MapIndexed[{EdgeForm[{Black, AbsoluteThickness[10/#2[[1]]]}], Opacity[1/#2[[1]]], #1} &, ResourceFunction["AlgebraicSubstitutionTiling"]["QuarterHex", 4, {"N", "Polygons"}]]]
Out[7]=

Neat Examples (5) 

The psi-quad substitution tiling is based on the Narayana cow sequence constant, ψ≈1.465571231876768, also called the super-golden ratio, shown here with sixteen levels of substitution:

In[8]:=
ResourceFunction[ "AlgebraicSubstitutionTiling"]["PsiQuad", 16, {"N", "ImageSize" -> 500}]
Out[8]=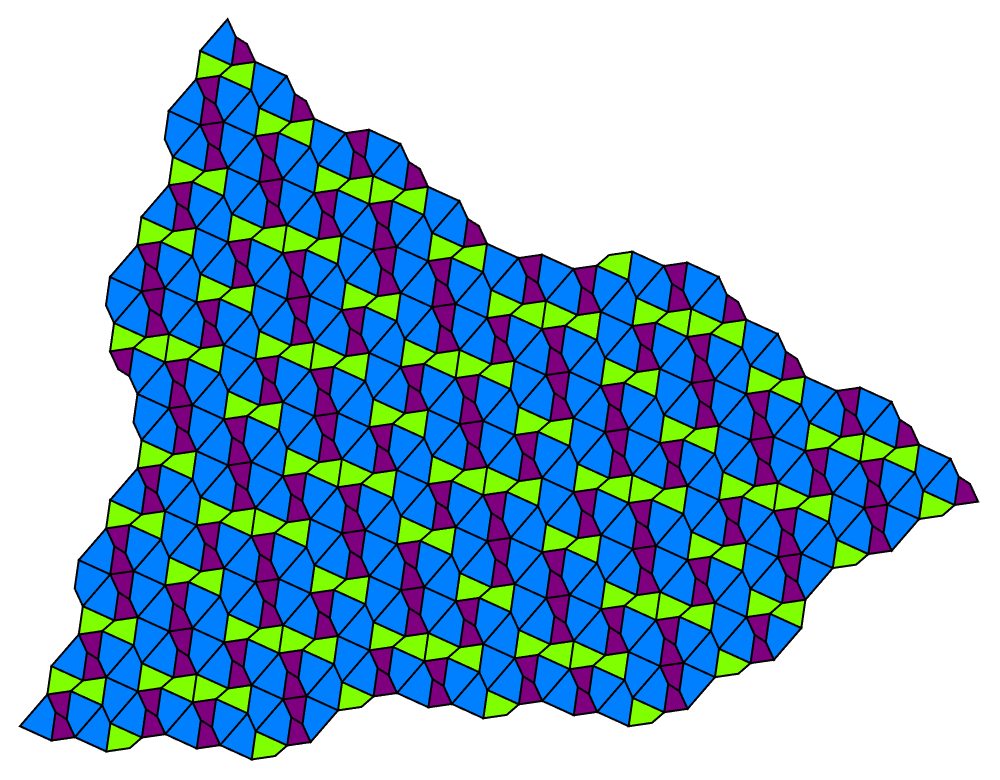

The rho-quad substitution tiling is based on the plastic constant, ρ≈1.324717957244746, shown here with thirteen levels of substitution on top of the initial tile:

In[9]:=
Show[Graphics[{EdgeForm[Black], Opacity[.6], #}] & /@ ResourceFunction["AlgebraicSubstitutionTiling"]["RhoQuad", 13, {"N", "Polygons"}][[{1, 13}]]]
Out[9]=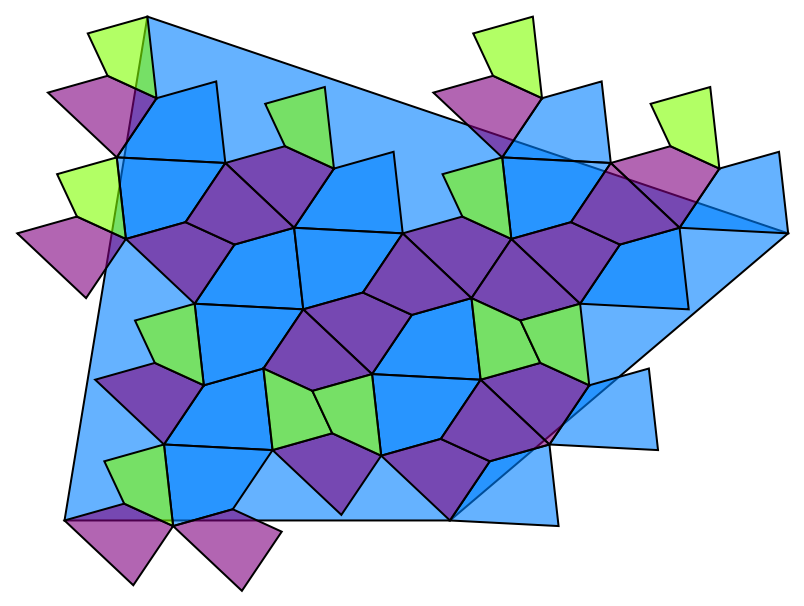

Use numeric approximation to show and compare growth with alternate starting positions for the Penrose rhombs and the Godrèche-Lançon binary tiling systems:

In[10]:=
Row[{ ResourceFunction["AlgebraicSubstitutionTiling"]["PenroseRhomb", 4, {"N", "Start" -> (Prepend[{#[[1]], GoldenRatio #[[2]], #[[3]]}, {0, 0}] & /@ Partition[CirclePoints[10], 3, 2, 1]), "ImageSize" -> 350}], ResourceFunction["AlgebraicSubstitutionTiling"]["Binary", 3, {"N", "Start" -> (Append[{#[[1]], GoldenRatio #[[2]], #[[3]]}, {0, 0}] & /@ Partition[CirclePoints[10], 3, 2, 1]), "ImageSize" -> 350}]}]
Out[10]=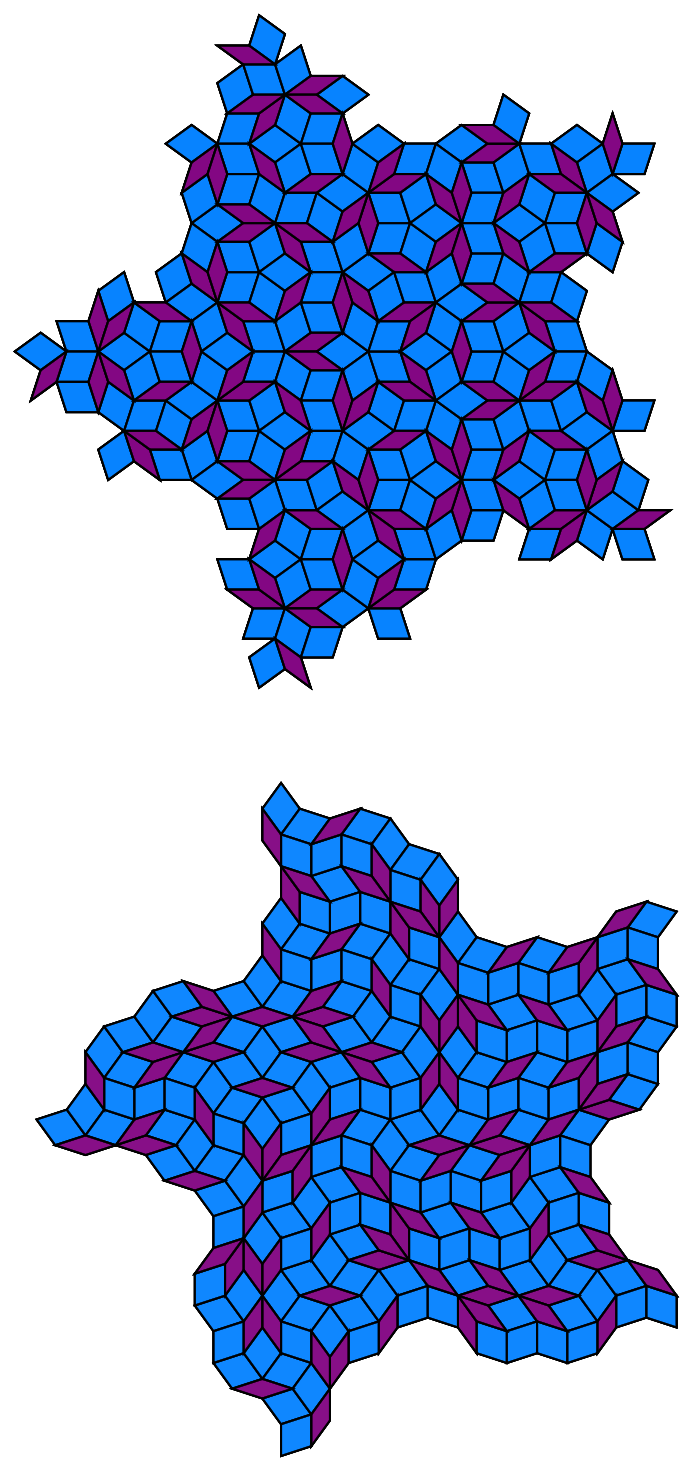

Tilings from the blog article Shattering the Plane with Twelve New Substitution Tilings Using 2, φ, ψ, χ, ρ:

In[11]:=
ResourceFunction["AlgebraicSubstitutionTiling"][#, 4, {"N", "ImageSize" -> 400}] & /@ {"SqrtTwo", "SqrtPhi", "SqrtPsi", "SqrtRho"}
Out[11]=

One of many variants of a tiling based on a root of χ4-χ-1=0:

In[12]:=
ResourceFunction[ "AlgebraicSubstitutionTiling"]["SqrtChi", 9, {"N", "ImageSize" -> 600}]
Out[12]=

Counts of the triangles of different sizes in the above tiling:

In[13]:=
Grid[Transpose[{#[[1]], Length[#[[2]]]} & /@ Last[ResourceFunction["AlgebraicSubstitutionTiling"]["SqrtChi", 9, {"N", "Polygons"}]]]]
Out[13]=

Requirements

Wolfram Language 11.3 (March 2018) or above

Version History

  • 2.0.0 – 03 April 2019
  • 1.0.0 – 27 March 2019

Related Resources

License Information