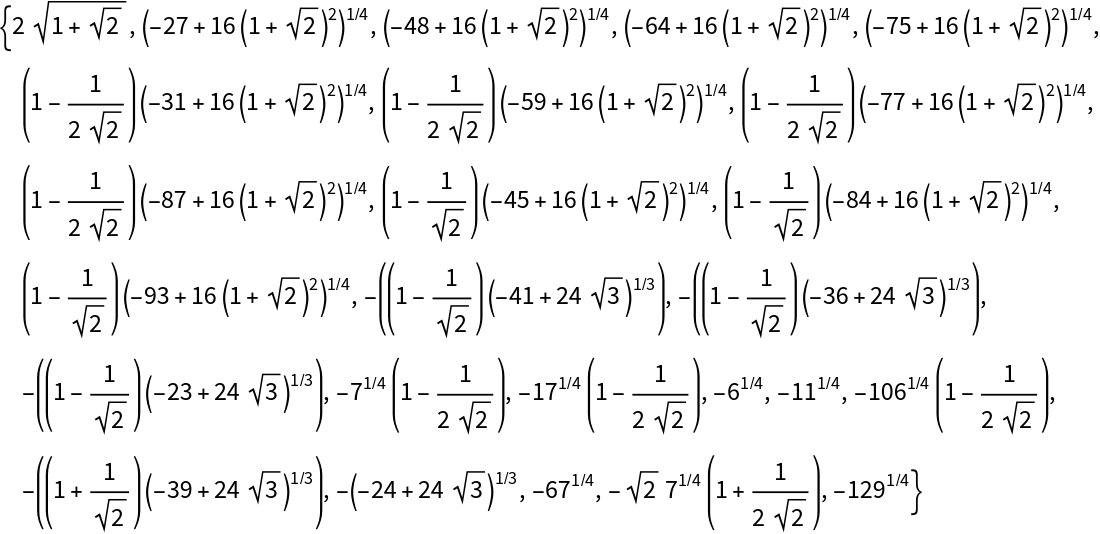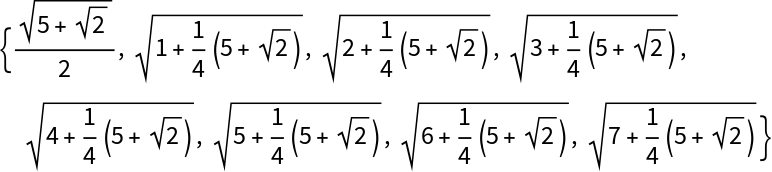Details and Options
AlgebraicRange creates ranges made of
algebraic numbers. This extends the basic concept of
Range to include, besides
Rational numbers, also roots, always restricted to the
Reals domain.
The first two arguments represent the bounds of the range (minimum and maximum values), while the optional third and fourth arguments (by default equal to 1 and 0) regulate the upper and lower bounds of the steps (differences between successive elements).
If no step parameter is specified, the elementary algebraic range
ResourceFunction["AlgebraicRange"][x,y] is determined by the square root range
Sqrt[Range[x^2,y^2]], for
x,y>0. The extension to negative bounds
x <0 or
y<0 is performed simply by reflection, since general real roots are mathematically defined only for positive arguments.
The step between successive algebraics is not straightforward to define univocally, as there exists no constant difference among the irrational numbers generated even with the elementary algebraic range. However, it turns out that an intuitively simple class of algebraic ranges, with non-unit step parameter
s, is obtained by taking the outer product of
ResourceFunction["AlgebraicRange"][Min[x,x/s],y] with
Join[ Range[Max[1, s], y, s],Range[Max[1, s], 0, -s]], for
s>0 and
0<=x<=y. Then the parameter
s also becomes the upper bound for all the steps. For example,
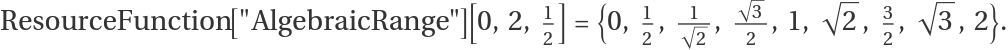
The algebraic numbers thus generated can often be in a great number, with a tendency to accumulate towards certain points. To avoid these features, a further fourth argument d can be optionally provided to require a minimum (absolute value) difference between successive algebraics, that is a lower bound for all the steps. This truncation process typically leads to a nearly uniform distribution of numeric values.
Extended functionality and syntax, especially for creating algebraic numbers of a more general form, are provided in the homonymous function of the paclet
DanieleGregori/GeneralizedRange.
A natural application of AlgebraicRange is in the search for closed forms for floating point numbers, possibly in terms of arbitrary combinations of mathematical functions with algebraic arguments, through ResourceFunction["
FindClosedForm"].
ResourceFunction["AlgebraicRange"] accepts the following options:
| "RootOrder" | 2 | the root orders to be included |
| "StepMethod" | "Outer" | change the method to define the step |
| "FareyRange" | False | generate algebraic numbers with steps given by the Farey sequence |
| "FormulaComplexity" | Infinity | set a complexity threshold over which the algebraics are discarded |
| "AlgebraicsOnly" | True | accept only algebraic arguments and output |
The option "RootOrder" can take the following values:
| r | include roots up to r order |
| {r} | include only roots of order r |
| {r1,r2,…} | include roots of all specified orders rk |
The option "StepMethod" can be used to define the step in ResourceFunction["AlgebraicRange"][x,y,s] and can take the following values:
| "Outer" | take the Outer product of ResourceFunction["AlgebraicRange"][Min[x,x/s],y] with Join[ Range[Max[1, s], y, s],Range[Max[1, s], 0, -s]] |
| "Root" | use Sqrt[Range[x^2,y^2,s^2]] |
A more detailed explanation of the step definition, also for negative bounds, can be found in the Properties and Relations Examples subsection.
Besides using the fourth argument to impose a lower bound on the steps, another way to restrict the output of AlgebraicRange is by setting a threshold for the complexity of the numeric expressions involved through the option "FormulaComplexity". The heuristic prescription for computing such complexity values is the following:
i) take all
Integers appearing in the algebraic expression;
ii) if a root or
Power appears, duplicate its argument a number of times equal to the root or power degree;
iii) if a negative integer or 0 appears, take its opposite and add 1;
iv) for each positive integer, compute the
Mean among its
DigitSum, 5 times its
IntegerLength, the total number of its
prime factors and the
square root of its absolute value;
v) normalize these means by multiplying them by 1/2 (so to let the numbers 0 and 1 have unit complexity);
vi) take the
Total of all these means.
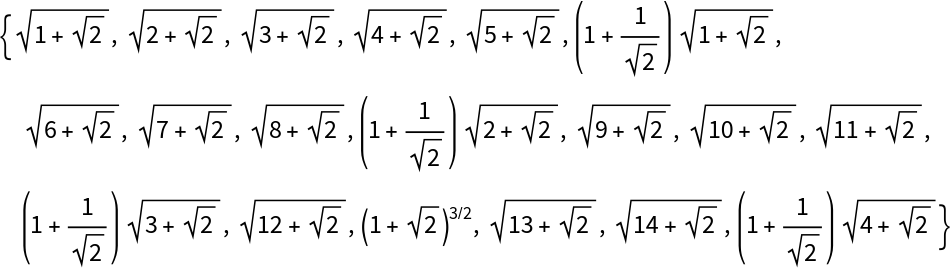
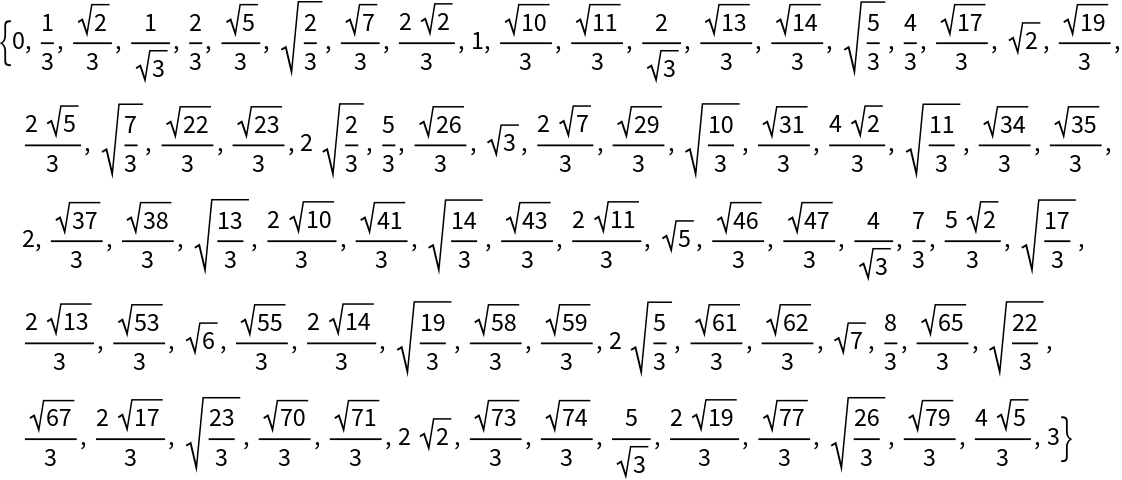
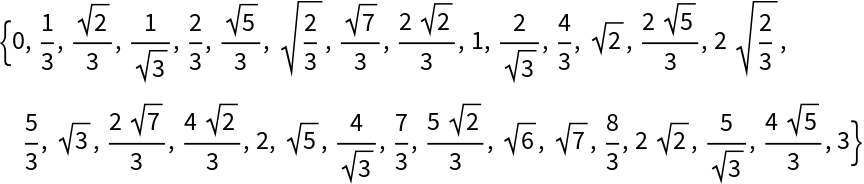
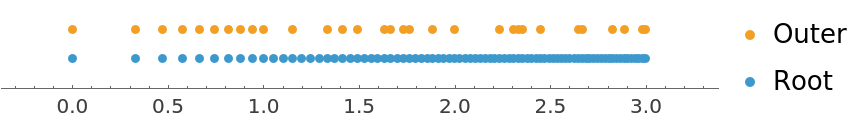
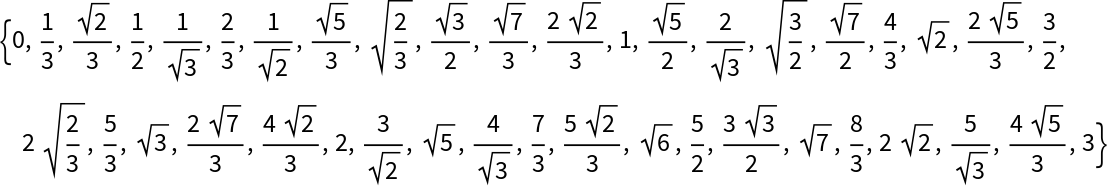
![SortBy[Union@
Flatten@Map[ResourceFunction["AlgebraicRange"][0, 3, #] &, %], N] ==
ResourceFunction["AlgebraicRange"][0, 3, 3, "FareyRange" -> True]](https://www.wolframcloud.com/obj/resourcesystem/images/f28/f2845916-4390-430d-b931-a23f7effc07c/13a195058b44cb66.png)
![ResourceFunction["FindClosedForm"][1.05592, BarnesG, "SearchRange" -> Function[ResourceFunction["AlgebraicRange"][-#, #, "RootOrder" -> 4]]]](https://www.wolframcloud.com/obj/resourcesystem/images/f28/f2845916-4390-430d-b931-a23f7effc07c/0c439cb611dbdce6.png)
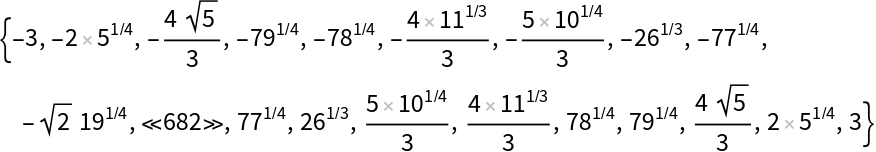
![ResourceFunction["FindClosedForm"][10.13051909, Identity, "SearchRange" -> Function[
Join[ResourceFunction["AlgebraicRange"][1, #, 1/2], ResourceFunction["AlgebraicRange"][Sqrt[1 + Sqrt[2]], #, 1/Sqrt[2]]]]]](https://www.wolframcloud.com/obj/resourcesystem/images/f28/f2845916-4390-430d-b931-a23f7effc07c/2360d2ce4eabedd3.png)
![Select[SortBy[
Outer[Times, Range[0, 3, 1/2], ResourceFunction["AlgebraicRange"][1, 3]] // Flatten // DeleteDuplicates, N], 1 <= # <= 3 &]](https://www.wolframcloud.com/obj/resourcesystem/images/f28/f2845916-4390-430d-b931-a23f7effc07c/1249b7ce4c045a55.png)
![Select[ReverseSortBy[
Outer[Times, Join[Range[1, 3, 1/Sqrt[3]], Range[1, 0, -1/Sqrt[3]]], Range[3^2, (3/2)^2, -1]^(1/2)] // Flatten // DeleteDuplicates, N],
3/2 <= # <= 3 &]](https://www.wolframcloud.com/obj/resourcesystem/images/f28/f2845916-4390-430d-b931-a23f7effc07c/0c9a8c239231a851.png)
![algrange = Block[{$MaxExtraPrecision = 10000}, ResourceFunction["AlgebraicRange"][
2 Sqrt[1 + Sqrt@RandomInteger[{2, 4}]], -2 Sqrt[
1 + Sqrt@RandomInteger[{2, 4}]], -Sqrt[2]/RandomInteger[{2, 4}], 1/4, "RootOrder" -> RandomInteger[{2, 5}, 2]]]](https://www.wolframcloud.com/obj/resourcesystem/images/f28/f2845916-4390-430d-b931-a23f7effc07c/03a5b951e743947a.png)