Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Compute the adjacency tensor of an arbitrary hypergraph
ResourceFunction["AdjacencyTensor"][h] gives the vertex adjacency tensor of the (ordered or orderless) hypergraph h. |
| "OrderedHyperedges" | False | whether to treat hyperedges as being ordered (directed) |
The adjacency tensor of an orderless hypergraph, with hyperedges of arity 3:
| In[1]:= |
|
| Out[1]= |
|
| In[2]:= |
|
| Out[2]= |
|
The adjacency tensor of an ordered hypergraph, with hyperedges of arity 3:
| In[3]:= |
|
| Out[3]= |
|
| In[4]:= |
|
| Out[4]= |
|
The adjacency tensor of an orderless hypergraph, with hyperedges of arity 5:
| In[5]:= |
|
| Out[5]= |
|
AdjacencyTensor supports multihypergraphs, in which case the tensor entries represent hyperedge multiplicities:
| In[6]:= |
|
| Out[6]= |
|
| In[7]:= |
|
| Out[7]= |
|
When the arity of hyperedges is equal to 2, the output of AdjacencyTensor is identical to the output of AdjacencyMatrix:
| In[8]:= |
|
| Out[8]= |
|
| In[9]:= |
|
| Out[9]= |
|
| In[10]:= |
|
| Out[10]= |
|
The adjacency tensor of an orderless hypergraph is always symmetric across all indices:
| In[11]:= |
|
| Out[11]= |
|
| In[12]:= |
|
| Out[12]= |
|
The adjacency tensor of an ordered hypergraph is not necessarily symmetric across all indices:
| In[13]:= |
|
| Out[13]= |
|
| In[14]:= |
|
| Out[14]= |
|
The adjacency tensor of a hypergraph with self-loops has diagonal entries:
| In[15]:= |
|
| Out[15]= |
|
| In[16]:= |
|
| Out[16]= |

|
| In[17]:= |
|
| Out[17]= |
|
Hyperedges can be of arbitrary arity:
| In[18]:= |
|
| Out[18]= |
|
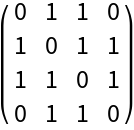
By default, all hyperedges are treated as orderless (i.e. undirected):
| In[19]:= |
|
| Out[19]= |
|
| In[20]:= |
|
| Out[20]= |
|
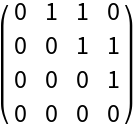
Use "OrderedHyperedges"→True to treat hyperedges as ordered (i.e. directed):
| In[21]:= |
|
| Out[21]= |
|
| In[22]:= |
|
| Out[22]= |
|
This work is licensed under a Creative Commons Attribution 4.0 International License