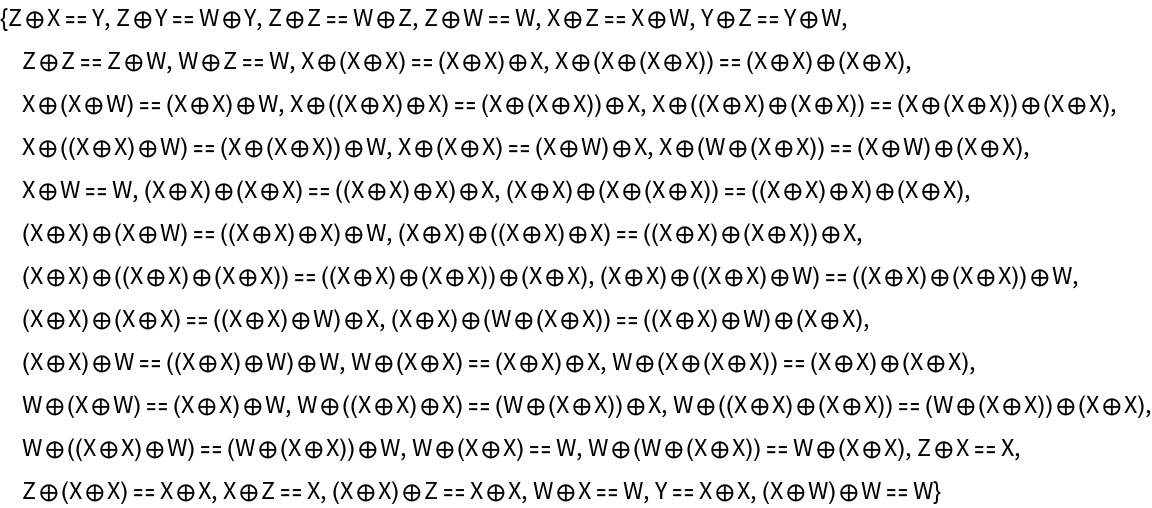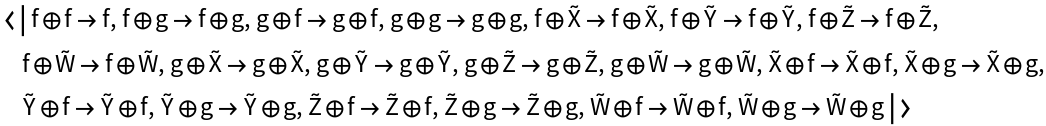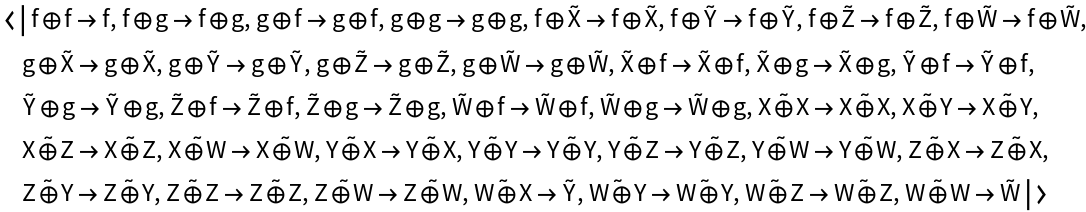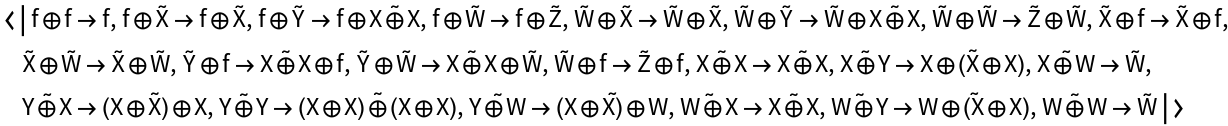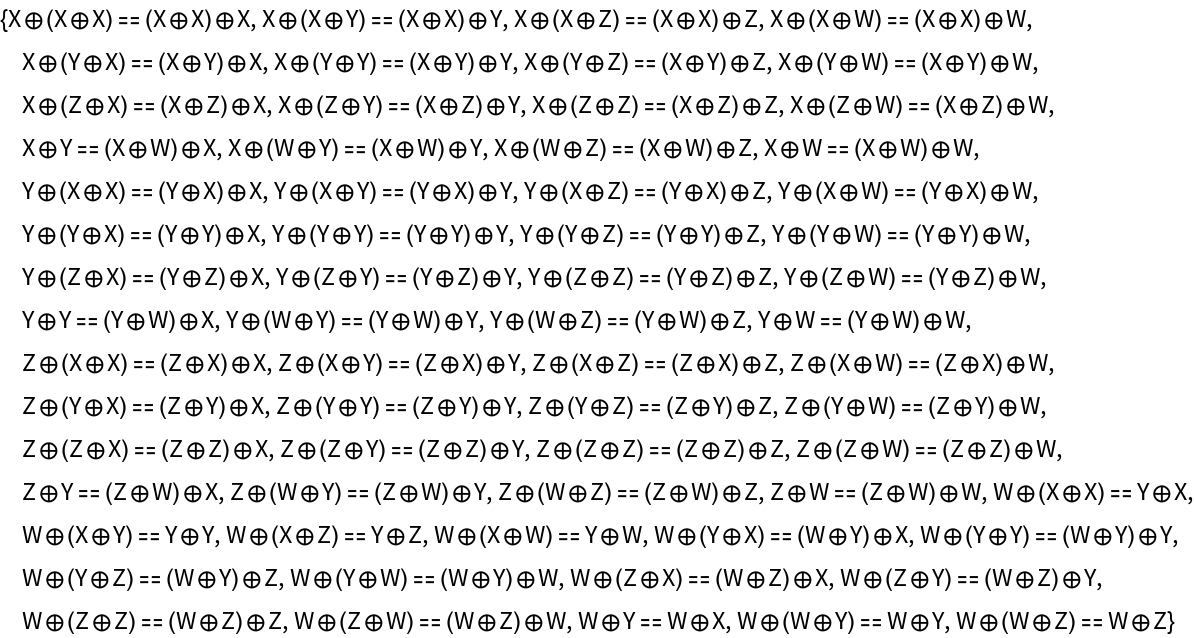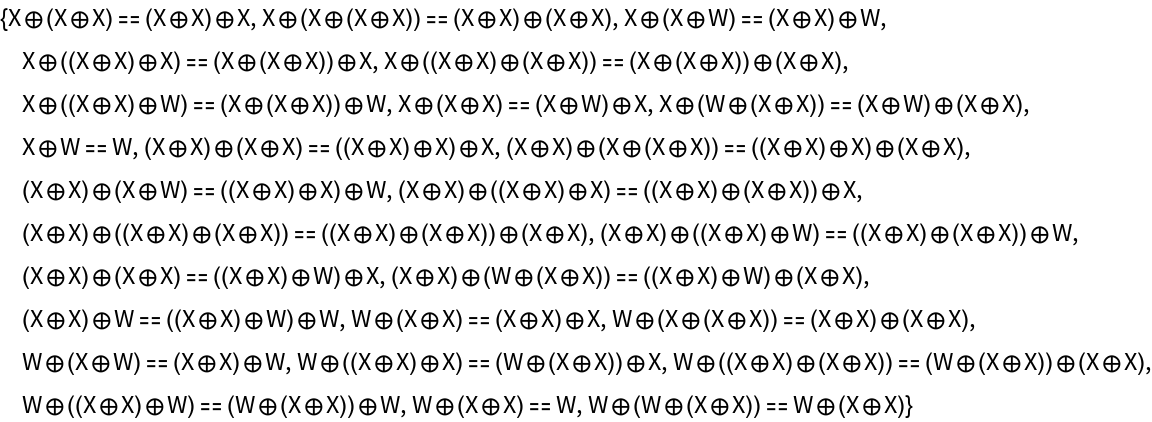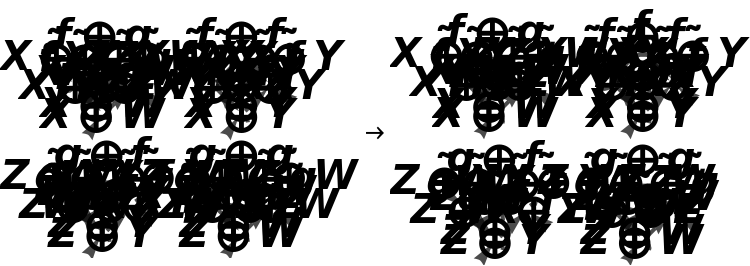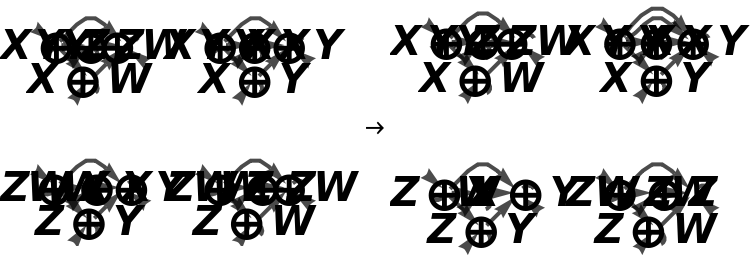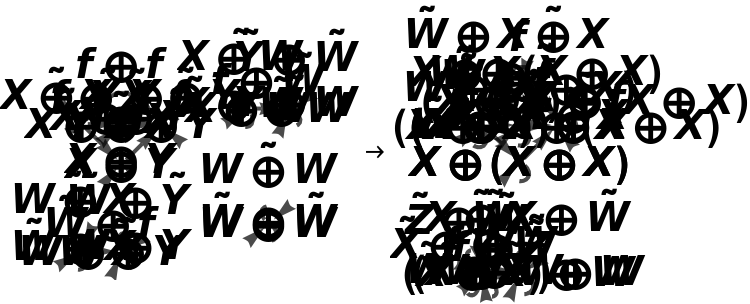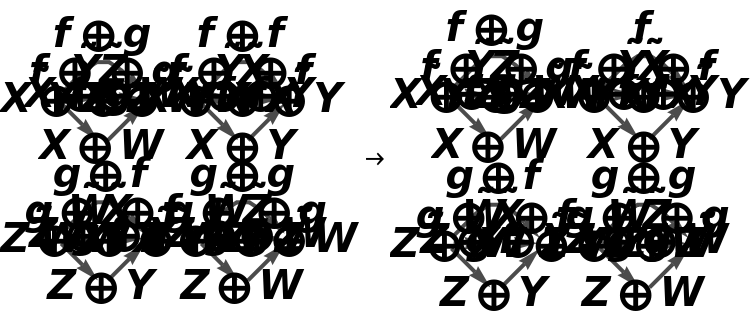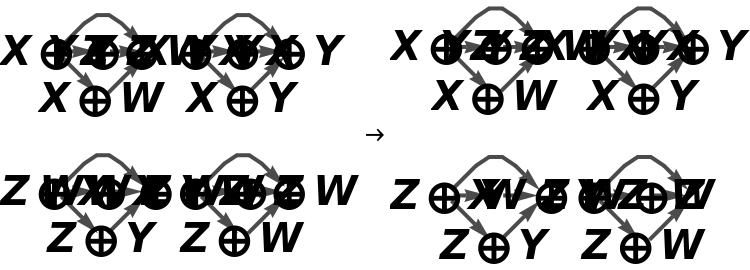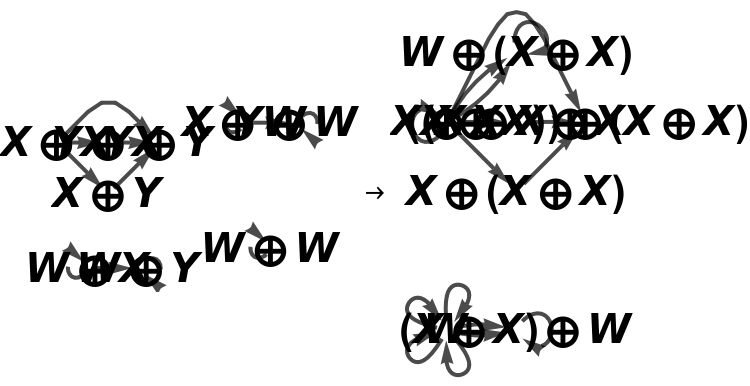Basic Examples (3)
Construct a simple abstract strict monoidal category from a trivial abstract category generated by a single arrow (with X being the distinguished unit object by default):
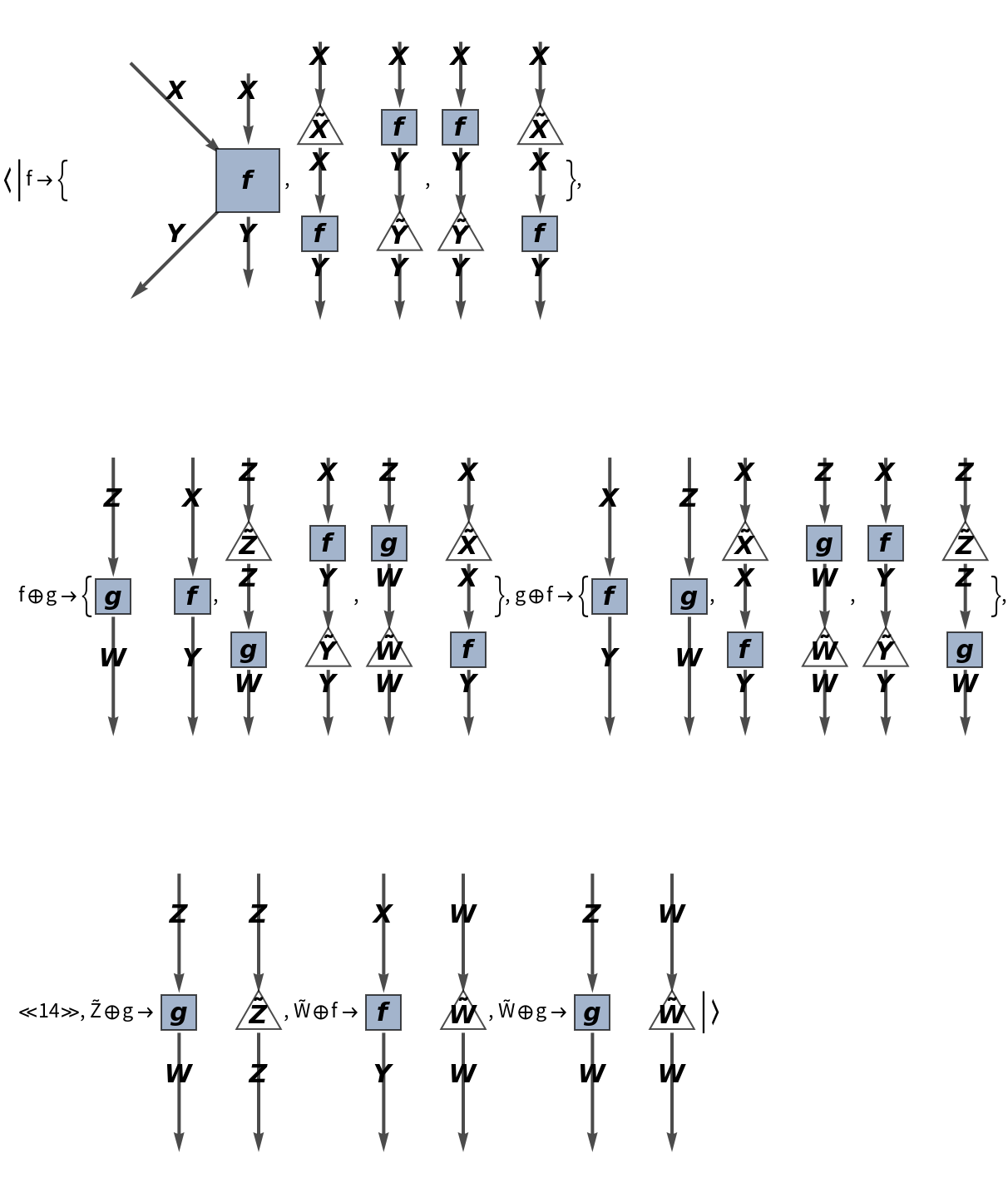
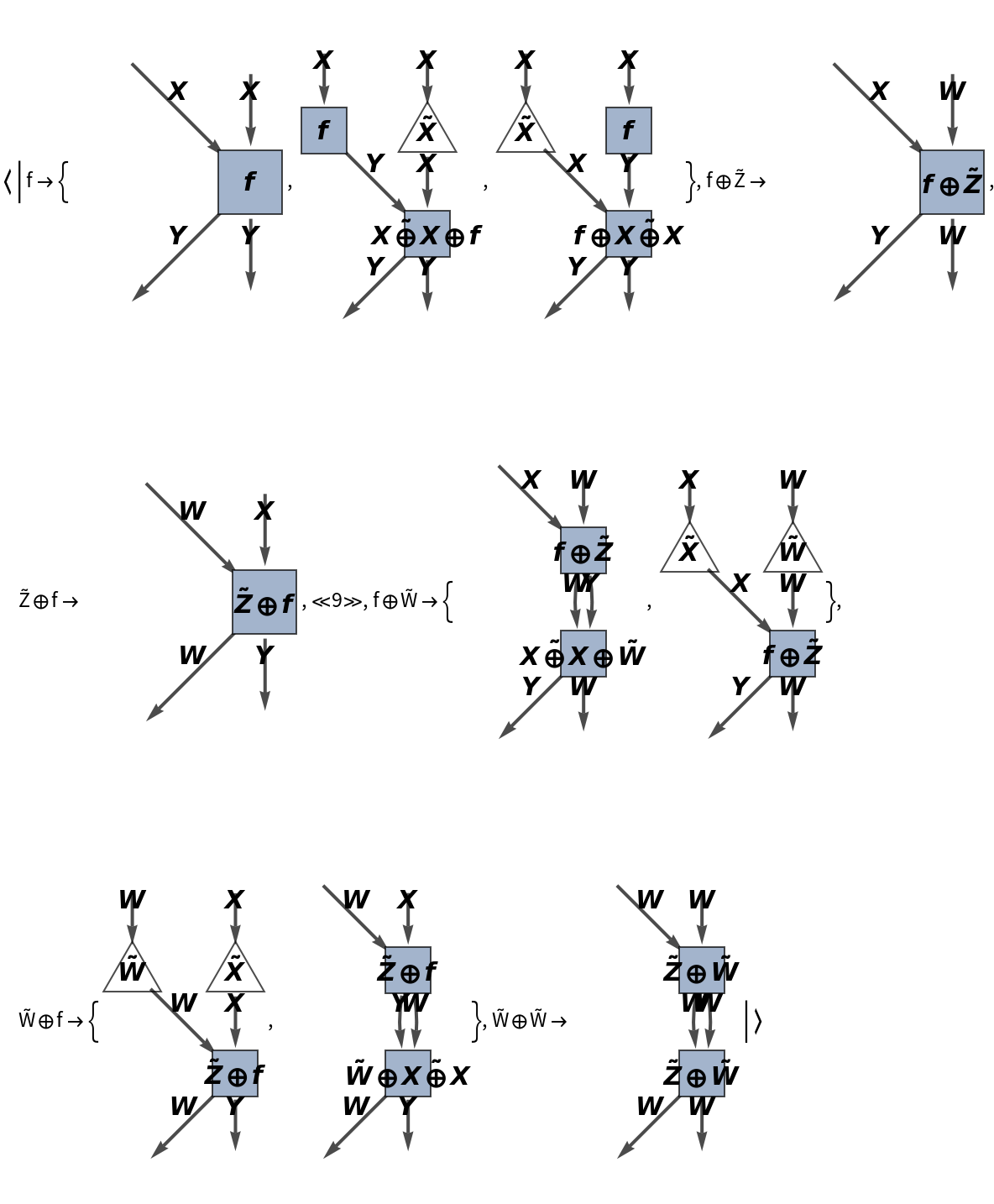
Show the full directed graph representation of the abstract bifunctor, with labels on the morphisms:
Show the full directed graphs without labels on the morphisms:
Show the list of associator equations (i.e. the equations characterizing the strict associativity of the tensor product structure):
Show the list of left and right unitor equations (i.e. the equations characterizing the fact that the distinguished unit object, namely X, acts as both a strict left identity and a strict right identity for the tensor product structure):
Show the reduced directed graph representation the abstract bifunctor, with all equivalences between objects and morphisms imposed and with labels on the morphisms:
Show the reduced directed graphs without labels on the morphisms:
Construct a new abstract strict monoidal category, but now with a pair of associations designating object/arrow mappings, and with tensor product symbol ⊕ and distinguished unit object Y:
Show that the resulting diagram is not commutative:
Compute the list of equations between morphisms that must hold for the diagram to be commutative (after all equivalences between objects and morphisms are imposed):
Construct a new abstract strict monoidal category with these new equations between morphisms imposed (and no corresponding equations between objects enforced):
Show that the resulting diagram is now commutative:
Show that the abstract strict monoidal category is not yet "valid" (i.e. the codomain of the abstract bifunctor does not yet match the underlying "base" category):
Construct a new abstract strict monoidal category with an additional equivalence between morphisms imposed in order to force validity:
Show that the abstract strict monoidal category is now valid:
Construct an abstract strict monoidal category from a simple abstract category in which object Y⊗Y is mapped to Y and object Z⊗Z is mapped to Z (with X being the distinguished unit object by default):
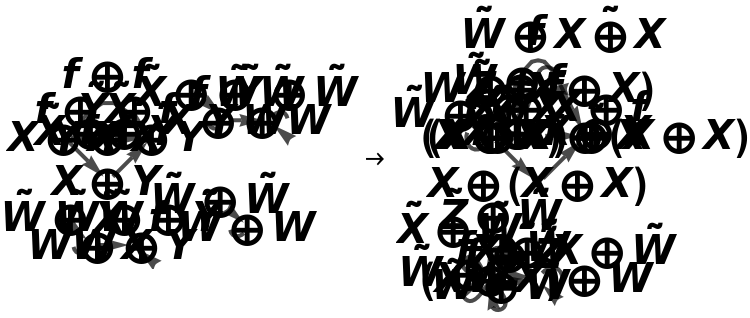
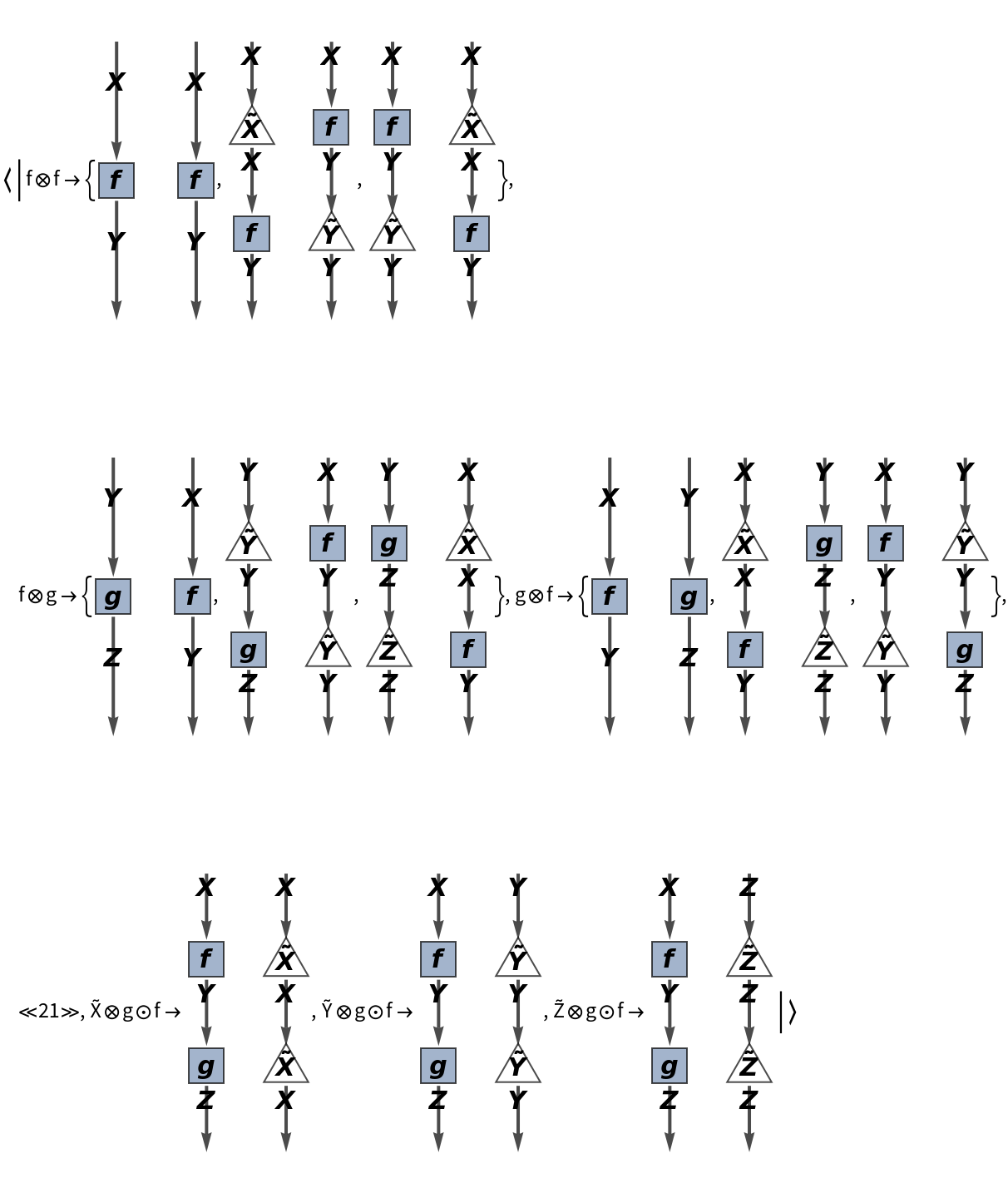
Show the association of monoidal string diagrams representing the (currently trivial) tensor product structure of each morphism, with labels on the wires and boxes:
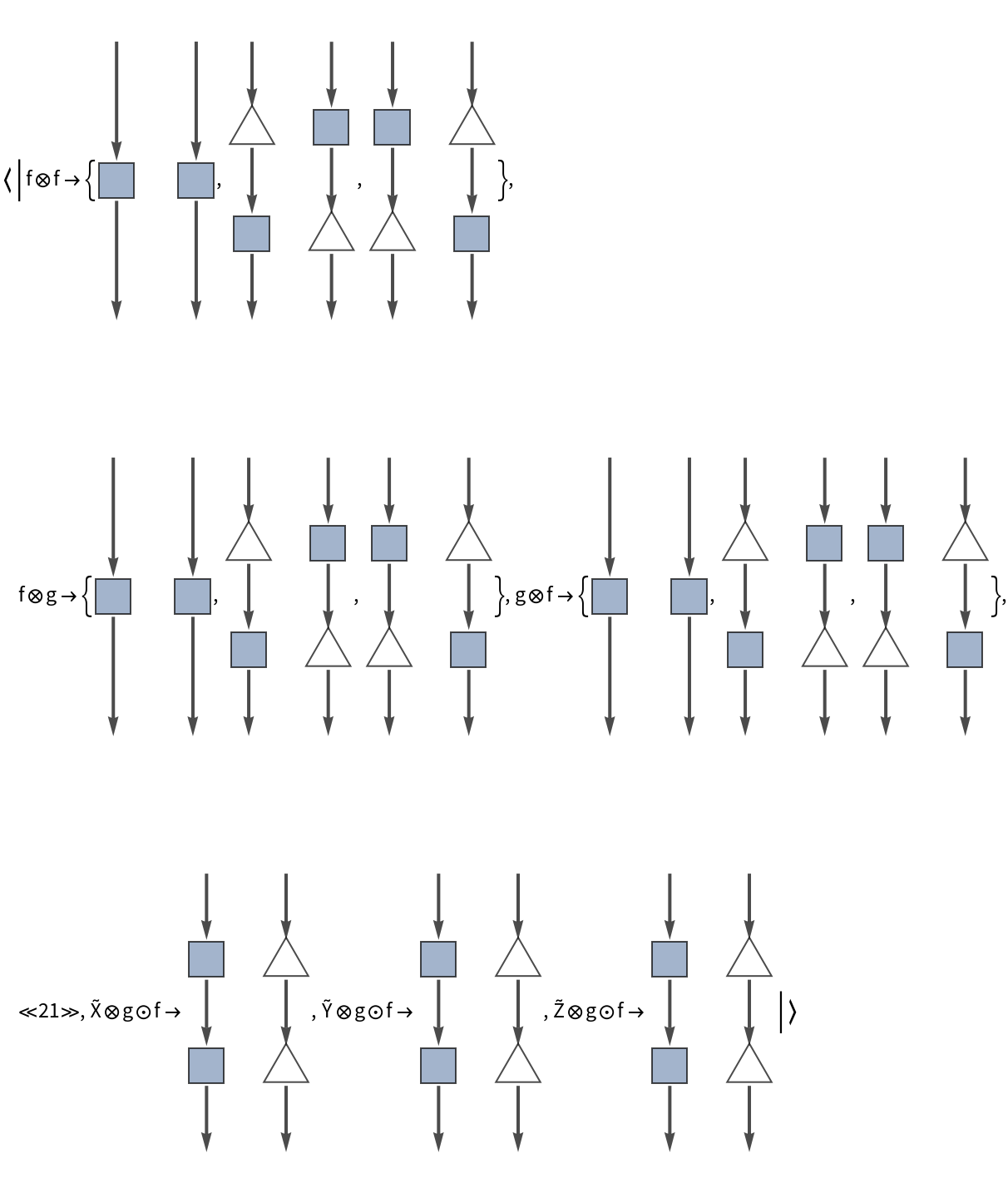
Show the association of monoidal string diagrams without labels on the wires and boxes:
Construct a new abstract strict monoidal category in which morphism f⊗f is mapped to F, morphism g⊗g is mapped to G, etc.:
Show the association of monoidal string diagrams representing the (now non-trivial) tensor product structure of each morphism, with labels on the wires and boxes:
Show the association of monoidal string diagrams without labels on the wires and boxes:
Show the association of object mappings:
Show the association of object mappings, with all equivalences between objects imposed:
Show the association of morphism mappings, with all equivalences between objects/morphisms imposed:
Compute the list of equations between morphisms that must hold for the diagram to be commutative (after all equivalences between objects and morphisms are imposed):
Construct a new abstract strict monoidal category in which, in addition to the object mappings above, objects (Z⊗Y)⊗Y and (Y⊗Z)⊗Z are both mapped to Z (with no corresponding morphism mappings):
Compute the list of equations between morphisms that must hold for the diagram to be commutative (after all equivalences between objects and morphisms are imposed):
Construct a new abstract strict monoidal category with these new equations between morphisms imposed (and no corresponding equations between objects enforced), plus three additional equivalences required to force validity:
Show that the resulting diagram is now commutative:
Show that the abstract strict monoidal category is now valid:
Show the association of monoidal string diagrams representing the tensor product structure of each morphism, with all equivalences between objects and morphisms imposed and with labels on the wires and boxes:
Show the association of monoidal string diagrams representing the tensor product structure of each morphism, with all equivalences between objects and morphisms imposed and without labels on the wires and boxes:
Construct an abstract strict monoidal category from a simple abstract category with equivalences between objects and morphisms, and show that these equivalences are subsequently inherited by the strict monoidal category by default:
Show the list of equivalences between objects:
Show the list of equivalences between morphisms:
Show the list of associator equations (i.e. the equations characterizing the strict associativity of the tensor product structure) after all equivalences between objects and morphisms are imposed:
Show the list of left and right unitor equations (i.e. the equations characterizing the fact that the distinguished unit object, namely X, acts as both a strict left identity and a strict right identity for the tensor product structure) after all equivalences between objects and morphisms are imposed:
Show the association of object mappings, with all equivalences between objects imposed:
Show the association of morphism mappings, with all equivalences between objects imposed:
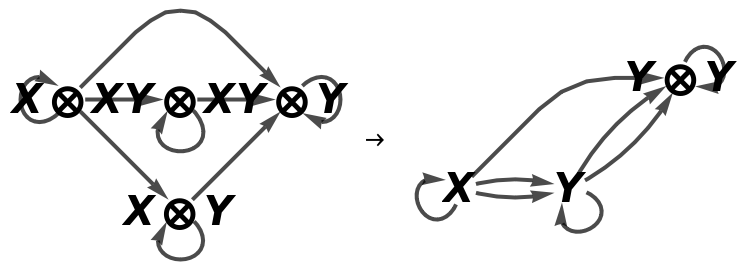
Show the association of monoidal string diagrams representing the (non-trivial) tensor product structure of each morphism, with all equivalences between objects and morphisms imposed and with labels on the wires and boxes:
Show the association of monoidal string diagrams representing the (non-trivial) tensor product structure of each morphism, with all equivalences between objects and morphisms imposed and without labels on the wires and boxes:
Show that the abstract strict monoidal category is (strictly) symmetric:
Show the list of equations between objects that must hold for the abstract strict monoidal category to be strictly symmetric:
Show the list of equations between objects that must hold for the abstract strict monoidal category to be strictly symmetric, with all equivalences between objects imposed:
Scope (2)
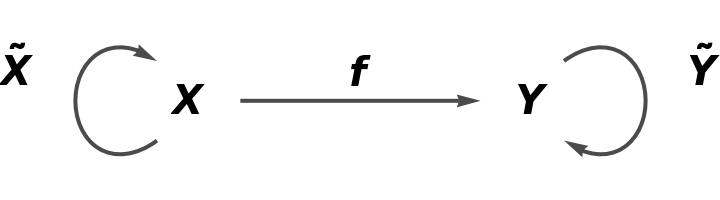
If AbstractStrictMonoidalCategory is given only an abstract category object, then its default behaviour is to construct an identity bifunctor on that category as the tensor product structure:
Additional arguments can be used to specify object and arrow mappings:
Further arguments can be used to specify the tensor product symbol and the distinguished unit object:
Further arguments can finally be used to specify new equivalences between objects and morphisms in the codomain category of the abstract bifunctor characterizing the strict monoidal category:
If the tensor product symbol is omitted, it is assumed to be ⊗ by default. If the distinguished unit object is omitted, it is assumed to be the canonically first object in the list of objects in the underlying abstract category by default:
New tensor product symbols and distinguished unit objects can be specified for any existing abstract strict monoidal category:
Likewise for new object and morphism equivalences:
All four properties (new tensor product symbol, new distinguished unit object, new object equivalences and new morphism equivalences) may be specified simultaneously:
From an explicit association:
Construct an abstract strict monoidal category from an abstract category and associations of object/arrow mappings, a tensor product symbol, a designated unit object and lists of new object/morphism equivalences:
Show the list of properties:
Show the number of objects in the domain category vs. the codomain category of the abstract bifunctor characterizing the abstract strict monoidal category:
Show the number of morphisms in the domain category vs. the codomain category of the abstract bifunctor characterizing the abstract strict monoidal category:
Show the list of equivalences between objects in the codomain category of the abstract bifunctor characterizing the abstract strict monoidal category:
Show the number of equivalences between objects in the codomain category of the abstract bifunctor characterizing the abstract strict monoidal category:
Show the list of equivalences between morphisms in the codomain category of the abstract bifunctor characterizing the abstract strict monoidal category:
Show the number of equivalences between morphisms in the codomain category of the abstract bifunctor characterizing the abstract strict monoidal category:
Show the number of reduced objects (modded out by all object equivalences) in the domain category vs. the codomain category of the abstract bifunctor characterizing the abstract strict monoidal category:
Show the number of reduced morphisms (modded out by all object and morphism equivalences) in the domain category vs. the codomain category of the abstract bifunctor characterizing the abstract strict monoidal category:
Show the (binary) symbol used to denote the tensor product structure in the abstract strict monoidal category:
Show the distinguished unit object in the abstract strict monoidal category:
Show the underlying "base" abstract category of the abstract strict monoidal category:
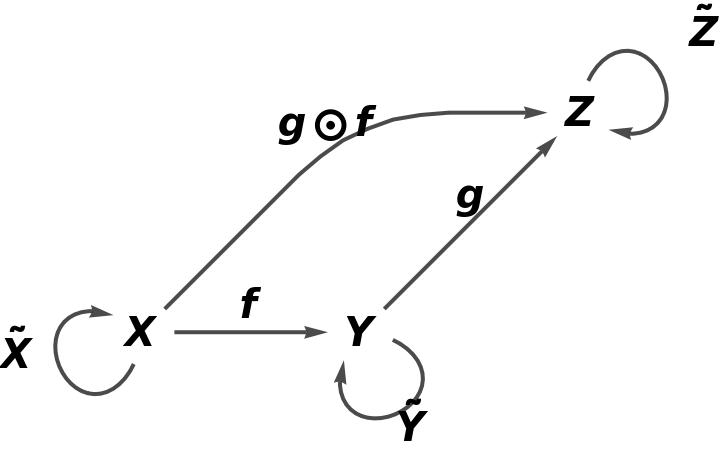
Compute the dual (obtained by swapping the source and target objects of each morphism and reversing the direction of morphism composition) of the abstract strict monoidal category:
Show the association of mappings between objects in the domain category and corresponding objects in the codomain category of the abstract bifunctor characterizing the abstract strict monoidal category:
Show the number of mappings between objects in the domain category and corresponding objects in the codomain category of the abstract bifunctor characterizing the abstract strict monoidal category:
Show the reduced association of mappings (modded out by all object equivalences) between objects in the domain category and corresponding objects in the codomain category of the abstract bifunctor characterizing the abstract strict monoidal category:
Show the number of reduced mappings (modded out by all object equivalences) between objects in the domain category and corresponding objects in the codomain category of the abstract bifunctor characterizing the abstract strict monoidal category:
Show the association of mappings between arrows in the underlying quiver of the domain category and corresponding arrows in the underlying quiver of the codomain category of the abstract bifunctor characterizing the abstract strict monoidal category:
Show the number of mappings between arrows in the underlying quiver of the domain category and corresponding arrows in the underlying quiver of the codomain category of the abstract bifunctor characterizing the abstract strict monoidal category:
Show the association of mappings between morphisms in the domain category and corresponding morphisms in the codomain category of the abstract bifunctor characterizing the abstract strict monoidal category:
Show the number of mappings between morphisms in the domain category and corresponding morphisms in the codomain category of the abstract bifunctor characterizing the abstract strict monoidal category:
Show the reduced association of mappings (modded out by all object and morphism equivalences) between morphisms in the domain category and corresponding morphisms in the codomain category of the abstract bifunctor characterizing the abstract strict monoidal category:
Show the number of reduced mappings (modded out by all object and morphism equivalences) between morphisms in the domain category and corresponding morphisms in the codomain category of the abstract bifunctor characterizing the abstract strict monoidal category:
Determine whether the abstract strict monoidal category is "valid" (i.e. the codomain of the abstract bifunctor characterizing the abstract strict monoidal category matches the underlying "base"abstract category):
Compute the association mapping morphisms in the abstract strict monoidal category to their corresponding monoidal string diagram representations, with labels on the wires and boxes:
Compute the association mapping morphisms in the abstract strict monoidal category to their corresponding monoidal string diagram representations, without labels on the wires and boxes:
Compute the association mapping morphisms in the abstract strict monoidal category to their corresponding monoidal string diagram representations, with all equivalences between objects and morphisms imposed and with labels on the wires and boxes:
Compute the association mapping morphisms in the abstract strict monoidal category to their corresponding monoidal string diagram representations, with all equivalences between objects and morphisms imposed and without labels on the morphisms:
Show the list of equations between objects in the abstract strict monoidal category implicitly imposed by the constraint that the tensor product structure must be strictly associative:
Show the list of equations between objects in the abstract strict monoidal category implicitly imposed by the constraint that the tensor product structure must be strictly associative, modulo all object and morphism equivalences:
Show the list of equations between objects in the abstract strict monoidal category implicitly imposed by the constraint that the distinguished unit object must act as a strict left identity for the tensor product structure:
Show the list of equations between objects in the abstract strict monoidal category implicitly imposed by the constraint that the distinguished unit object must act as a strict left identity for the tensor product structure, modulo all object and morphism equivalences:
Show the list of equations between objects in the abstract strict monoidal category implicitly imposed by the constraint that the distinguished unit object must act as a strict right identity for the tensor product structure:
Show the list of equations between objects in the abstract strict monoidal category implicitly imposed by the constraint that the distinguished unit object must act as a strict right identity for the tensor product structure, modulo all object and morphism equivalences:
Determine whether the abstract strict monoidal category is a commutative diagram (i.e. all directed paths through the graph with the same source and target object yield the same morphism):
Show the list of equations between morphisms required to force the abstract strict monoidal category to be a commutative diagram:
Show the list of equations between morphisms required to force the abstract strict monoidal category to be a commutative diagram, modulo all equivalences between objects and morphisms:
Determine whether the abstract strict monoidal category is strictly symmetric (i.e. the tensor product structure is strictly commutative):
Show the list of equations between objects required to force the abstract strict monoidal category to be strictly symmetric:
Show the list of equations between objects required to force the abstract strict monoidal category to be strictly symmetric, modulo all equivalences between objects and morphisms:
Show the abstract bifunctor characterizing the abstract strict monoidal category, represented as a map between full directed graphs with labels on the morphisms:
Show the abstract bifunctor characterizing the abstract strict monoidal category, represented as a map between full directed graphs without labels on the morphisms:
Show the abstract bifunctor characterizing the abstract strict monoidal category, represented as a map between reduced directed graphs, with all equivalences between objects and morphisms imposed and with labels on the morphisms:
Show the abstract bifunctor characterizing the abstract strict monoidal category, represented as a map between reduced directed graphs, with all equivalences between objects and morphisms imposed and without labels on the morphisms:
Show the abstract bifunctor characterizing the abstract strict monoidal category, represented as a map between simple directed graphs, with all self-loops and multiedges removed and with labels on the morphisms:
Show the abstract bifunctor characterizing the abstract strict monoidal category, represented as a map between simple directed graphs, with all self-loops and multiedges removed and without labels on the morphisms:
Show the abstract bifunctor characterizing the abstract strict monoidal category, represented as a map between reduced simple directed graphs, with all self-loops and multiedges removed, plus all object and morphism equivalences modded out and with labels on the morphisms:
Show the abstract bifunctor characterizing the abstract strict monoidal category, represented as a map between reduced simple directed graphs, with all self-loops and multiedges removed, plus all object and morphism equivalences modded out and without labels on the morphisms:
Show the explicit association form of the abstract strict monoidal category:
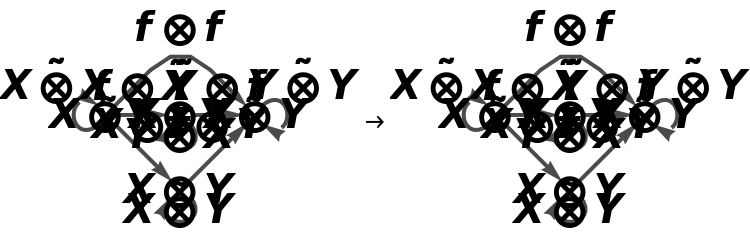
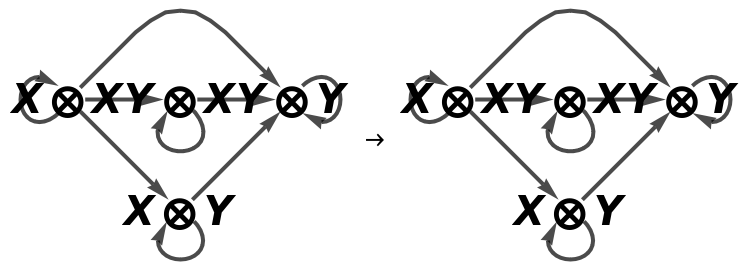
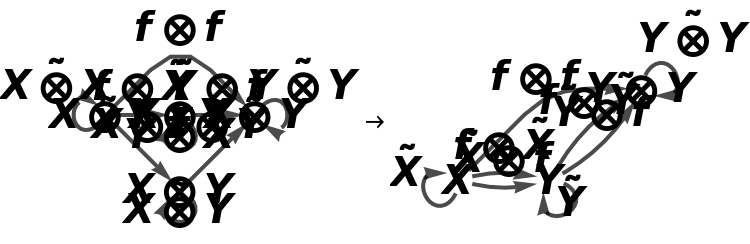
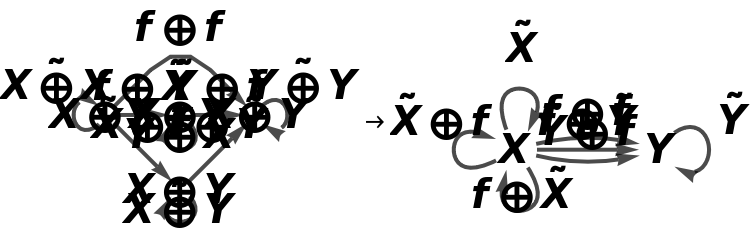
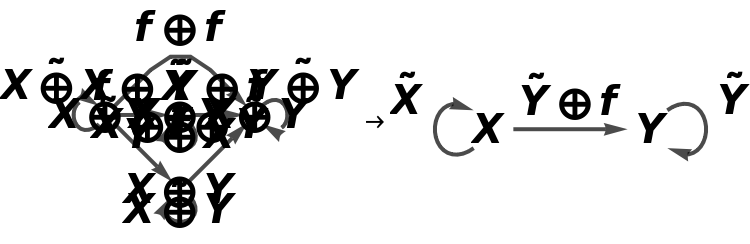
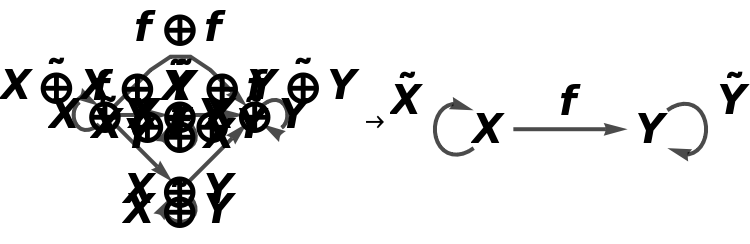
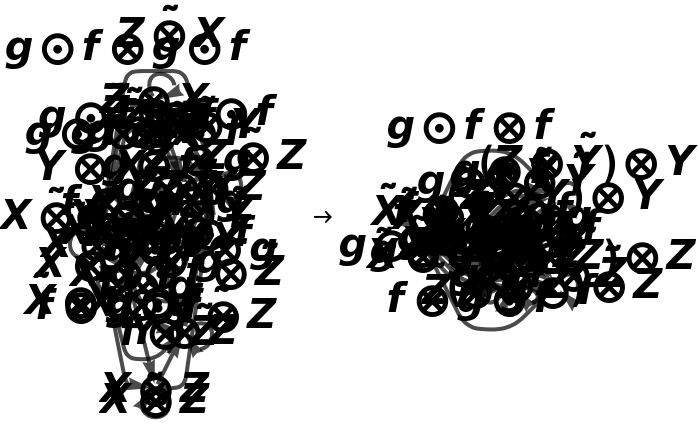
![monoidalCategory2 = ResourceFunction["AbstractStrictMonoidalCategory"][
category, <|CircleTimes[Y, Y] -> Y, CircleTimes[Z, Z] -> Z|>, <|
CircleTimes[f, f] -> F, CircleTimes[g, g] -> G, CircleTimes[f, OverTilde[X]] -> fX, CircleTimes[OverTilde[Y], g] -> Yg|>]](https://www.wolframcloud.com/obj/resourcesystem/images/8a4/8a437d89-ddef-4df3-b3a0-40bf06aa29c3/7547cbe0af84ab6d.png)
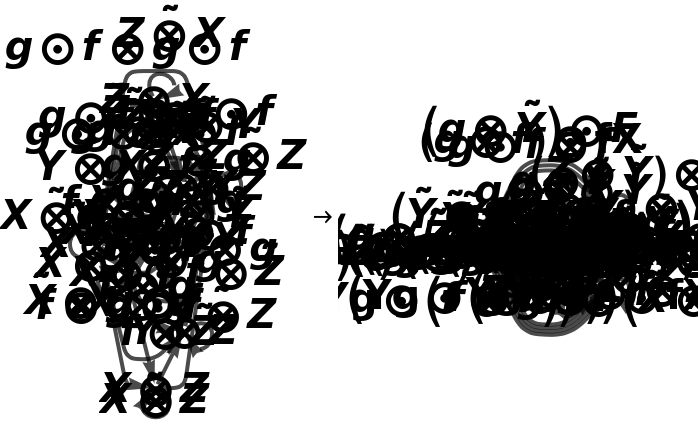


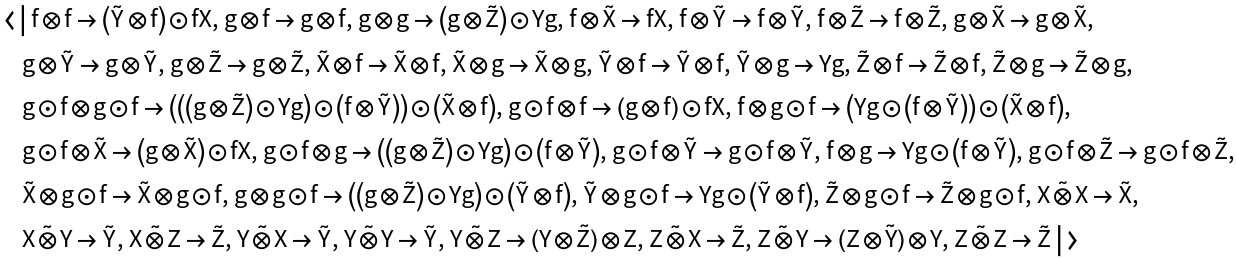
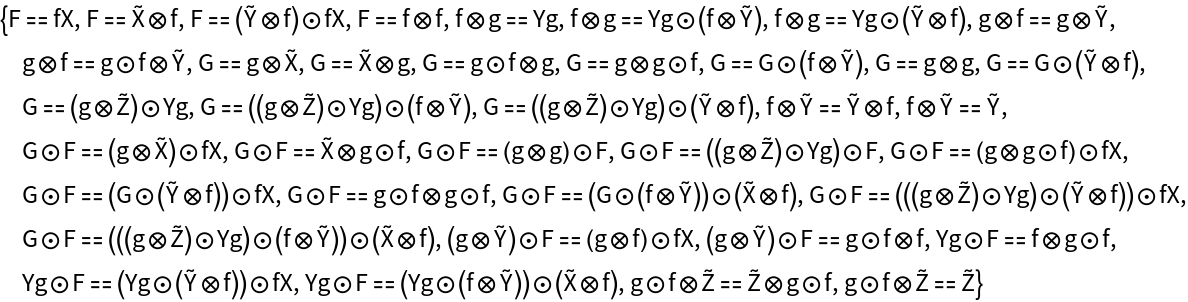
![monoidalCategory3 = ResourceFunction["AbstractStrictMonoidalCategory"][
category, <|CircleTimes[Y, Y] -> Y, CircleTimes[Z, Z] -> Z, CircleTimes[CircleTimes[Z, Y], Y] -> Z, CircleTimes[CircleTimes[Y, Z], Z] -> Z|>, <||>]](https://www.wolframcloud.com/obj/resourcesystem/images/8a4/8a437d89-ddef-4df3-b3a0-40bf06aa29c3/27aaedc72015226e.png)
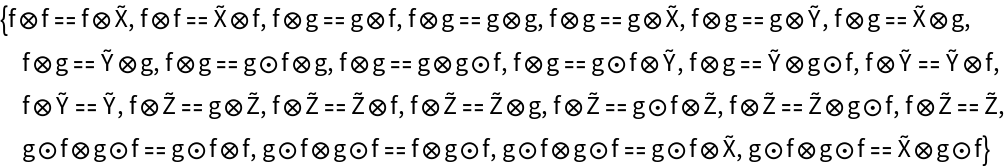
![monoidalCategory4 = ResourceFunction["AbstractStrictMonoidalCategory"][
category, <|CircleTimes[Y, Y] -> Y, CircleTimes[Z, Z] -> Z, CircleTimes[CircleTimes[Z, Y], Y] -> Z, CircleTimes[CircleTimes[Y, Z], Z] -> Z|>, <||>, {}, Join[equations, {CircleTimes[OverTilde[X], f] == f, CircleTimes[OverTilde[Y], CircleDot[g, f]] == g, CircleTimes[OverTilde[X], CircleDot[g, f]] == CircleDot[g, f]}]]](https://www.wolframcloud.com/obj/resourcesystem/images/8a4/8a437d89-ddef-4df3-b3a0-40bf06aa29c3/23208dd6cd61bd43.png)
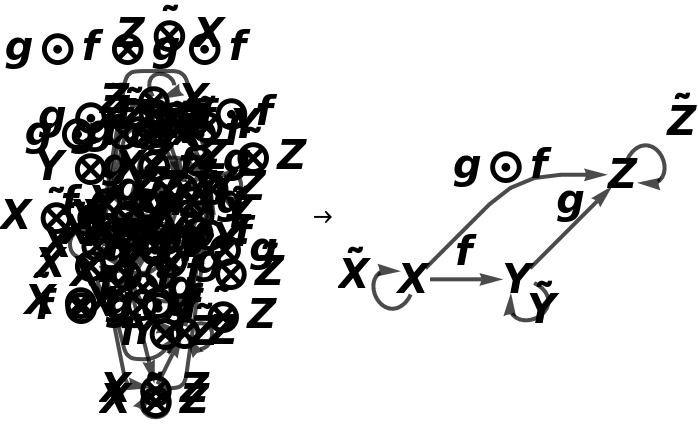

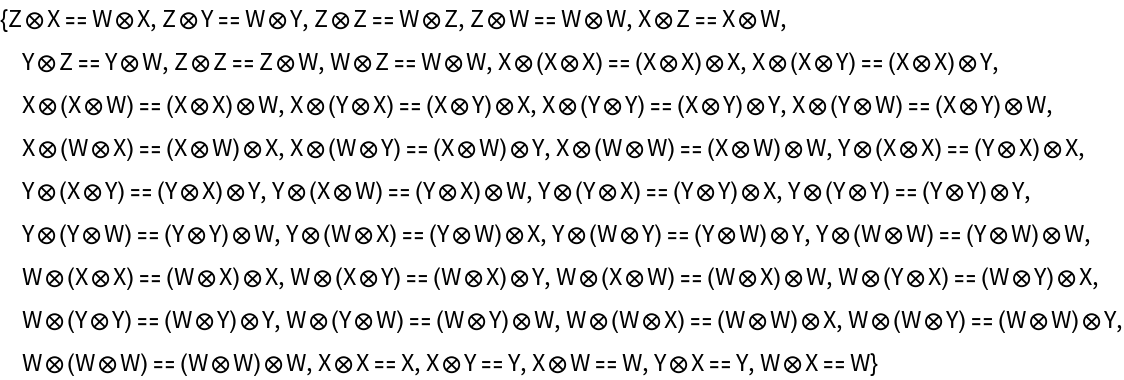
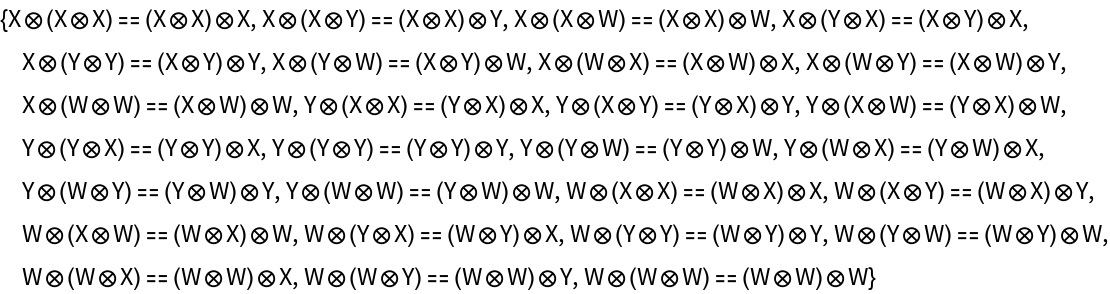
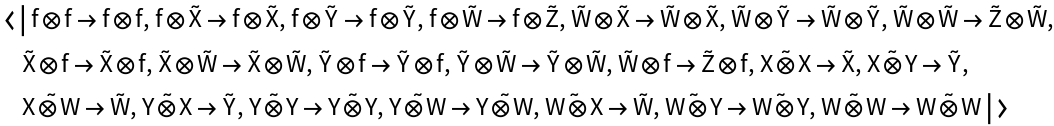


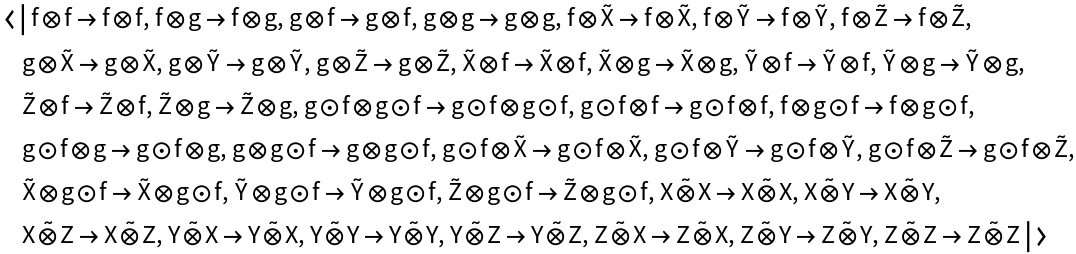
![monoidalCategory2 = ResourceFunction["AbstractStrictMonoidalCategory"][
category, <|CircleTimes[Y, Z] -> Y, CircleTimes[Z, Y] -> Z|>, <|
CircleTimes[f, g] -> f, CircleTimes[g, f] -> g|>]](https://www.wolframcloud.com/obj/resourcesystem/images/8a4/8a437d89-ddef-4df3-b3a0-40bf06aa29c3/6b28ece36bb0ecc5.png)
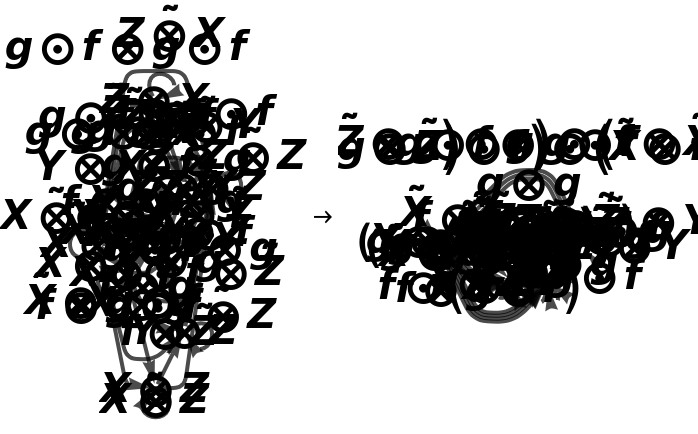
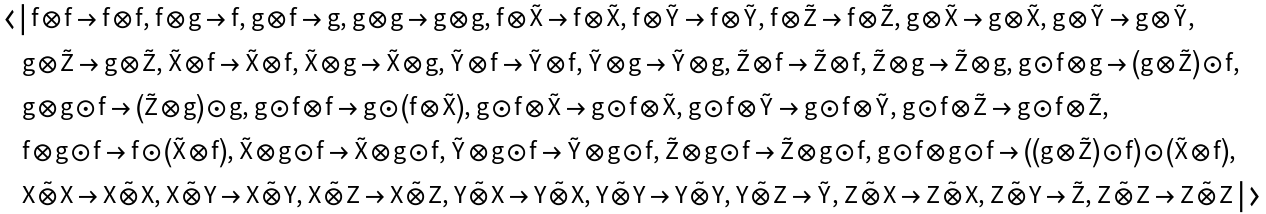
![monoidalCategory3 = ResourceFunction["AbstractStrictMonoidalCategory"][
category, <|CirclePlus[Y, X] -> Y, CirclePlus[X, Y] -> X|>, <|
CirclePlus[f, g] -> f, CirclePlus[g, f] -> g|>, CirclePlus, Z]](https://www.wolframcloud.com/obj/resourcesystem/images/8a4/8a437d89-ddef-4df3-b3a0-40bf06aa29c3/70707b9f50a2d8b2.png)
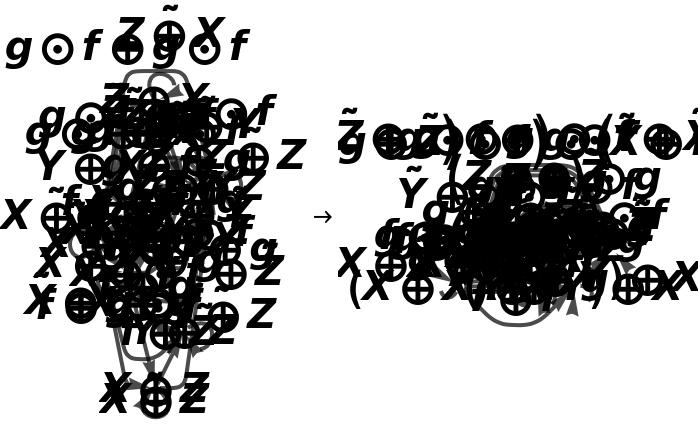
![monoidalCategory4 = ResourceFunction["AbstractStrictMonoidalCategory"][
category, <|CirclePlus[Y, X] -> Y, CirclePlus[X, Y] -> X|>, <|
CirclePlus[f, g] -> f, CirclePlus[g, f] -> g|>, CirclePlus, Z, {CirclePlus[CirclePlus[X, X], Y] == Y}, {CirclePlus[g, OverTilde[Y]] == CirclePlus[OverTilde[Y], g]}]](https://www.wolframcloud.com/obj/resourcesystem/images/8a4/8a437d89-ddef-4df3-b3a0-40bf06aa29c3/5b3f21eef4cff121.png)
![monoidalCategory5 = ResourceFunction["AbstractStrictMonoidalCategory"][
category, <|CircleTimes[Y, Z] -> Y, CircleTimes[Z, Y] -> Z|>, <|
CircleTimes[f, g] -> f, CirclePlus[g, f] -> g|>, {CircleTimes[CircleTimes[Z, Z], Y] == Y}, {CircleTimes[g, OverTilde[Y]] == CircleTimes[OverTilde[Y], g]}]](https://www.wolframcloud.com/obj/resourcesystem/images/8a4/8a437d89-ddef-4df3-b3a0-40bf06aa29c3/5973ee8026f8e33d.png)
![monoidalCategory7 = ResourceFunction["AbstractStrictMonoidalCategory"][
monoidalCategory5, {CircleTimes[CircleTimes[Z, Z], Y] == Y, CircleTimes[CircleTimes[Y, Y], Z] == Y}, {CircleTimes[g, OverTilde[Y]] == CircleTimes[OverTilde[Y], g],
CircleTimes[CircleDot[g, f], f] == CircleTimes[CircleDot[g, f], OverTilde[X]]}]](https://www.wolframcloud.com/obj/resourcesystem/images/8a4/8a437d89-ddef-4df3-b3a0-40bf06aa29c3/7fbf2bb3b0704e70.png)
![monoidalCategory8 = ResourceFunction["AbstractStrictMonoidalCategory"][monoidalCategory5,
CirclePlus, Z, {CirclePlus[X, X] == X, CirclePlus[Y, Y] == Y}, {CirclePlus[CircleDot[g, f], CircleDot[g, f]] == CirclePlus[CircleDot[g, f], OverTilde[Z]]}]](https://www.wolframcloud.com/obj/resourcesystem/images/8a4/8a437d89-ddef-4df3-b3a0-40bf06aa29c3/6238e7076fdd5e7f.png)


![monoidalCategory9 = ResourceFunction[
"AbstractStrictMonoidalCategory"][<|"Category" -> category, "ObjectMappings" -> <|CirclePlus[Y, Z] -> Y, CirclePlus[Z, Y] -> Z|>,
"ArrowMappings" -> <|CirclePlus[f, g] -> f, CirclePlus[g, f] -> g|>,
"TensorProductSymbol" -> CirclePlus, "UnitObject" -> Z, "ObjectEquivalences" -> {CirclePlus[X, X] == X, CirclePlus[Y, Y] == Y}, "MorphismEquivalences" -> {CirclePlus[CircleDot[g, f], CircleDot[g, f]] == CirclePlus[CircleDot[g, f], OverTilde[Z]]}|>]](https://www.wolframcloud.com/obj/resourcesystem/images/8a4/8a437d89-ddef-4df3-b3a0-40bf06aa29c3/70067747cfad9148.png)

![monoidalCategory = ResourceFunction["AbstractStrictMonoidalCategory"][
category, <|CirclePlus[W, W] -> W, CirclePlus[W, X] -> Y|>, <|
CirclePlus[f, f] -> f|>, CirclePlus, Z, {CirclePlus[W, X] == W, Y == CirclePlus[X, X], CirclePlus[CirclePlus[X, W], W] == W}, {CirclePlus[f, f] == f}]](https://www.wolframcloud.com/obj/resourcesystem/images/8a4/8a437d89-ddef-4df3-b3a0-40bf06aa29c3/0db870df55c26c7c.png)