Basic Examples (6)
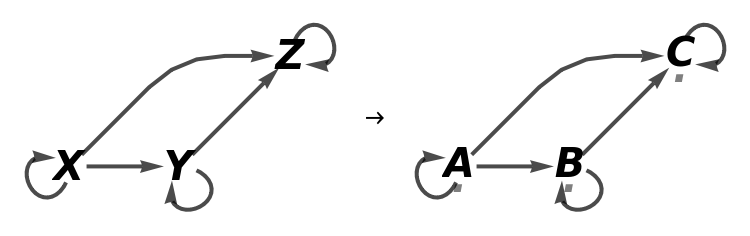
Construct a simple abstract functor from an abstract category and a pair of associations designating object/arrow mappings:
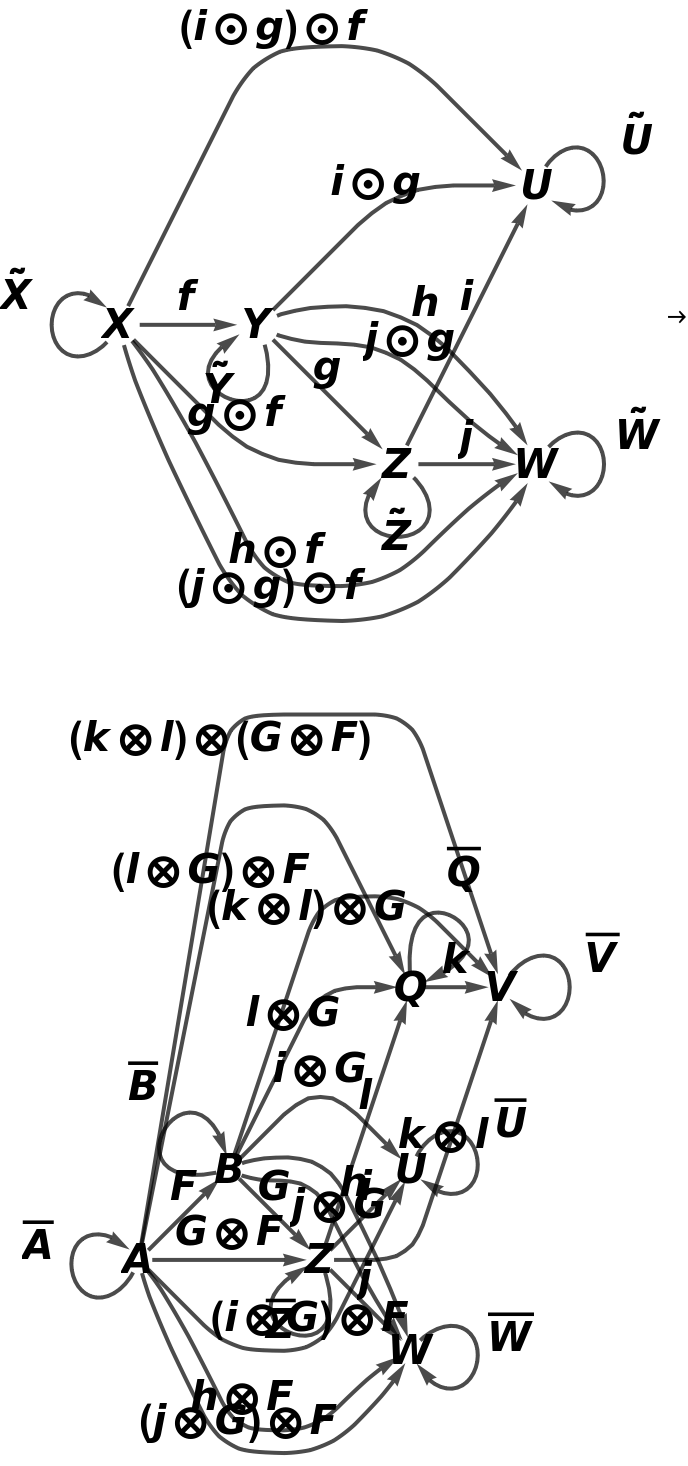
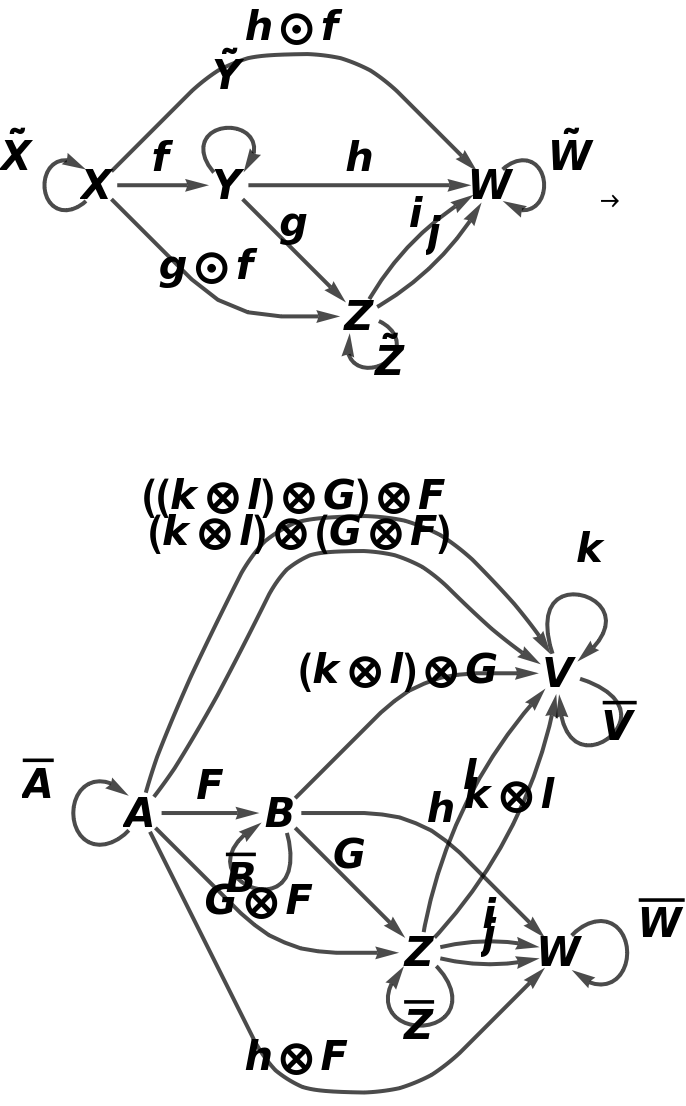
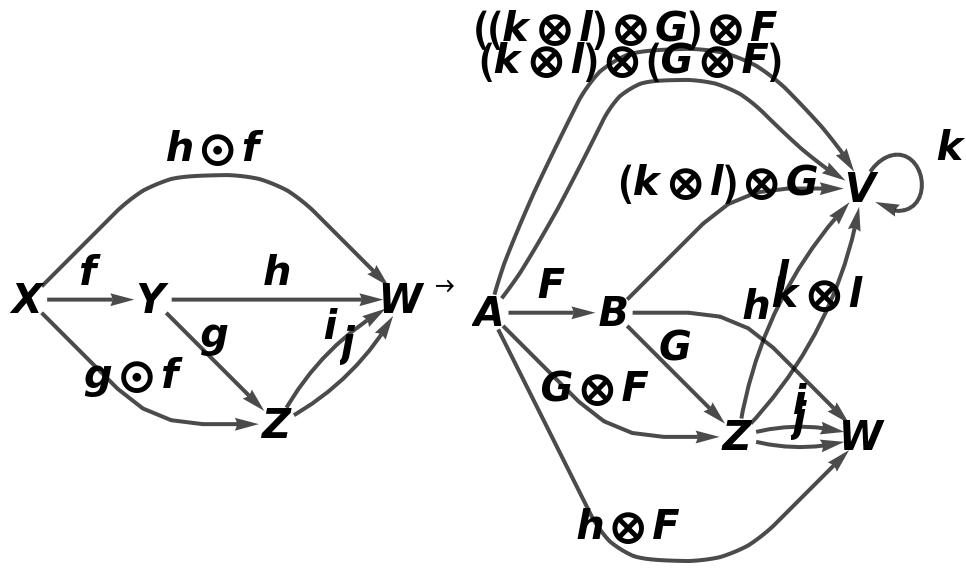
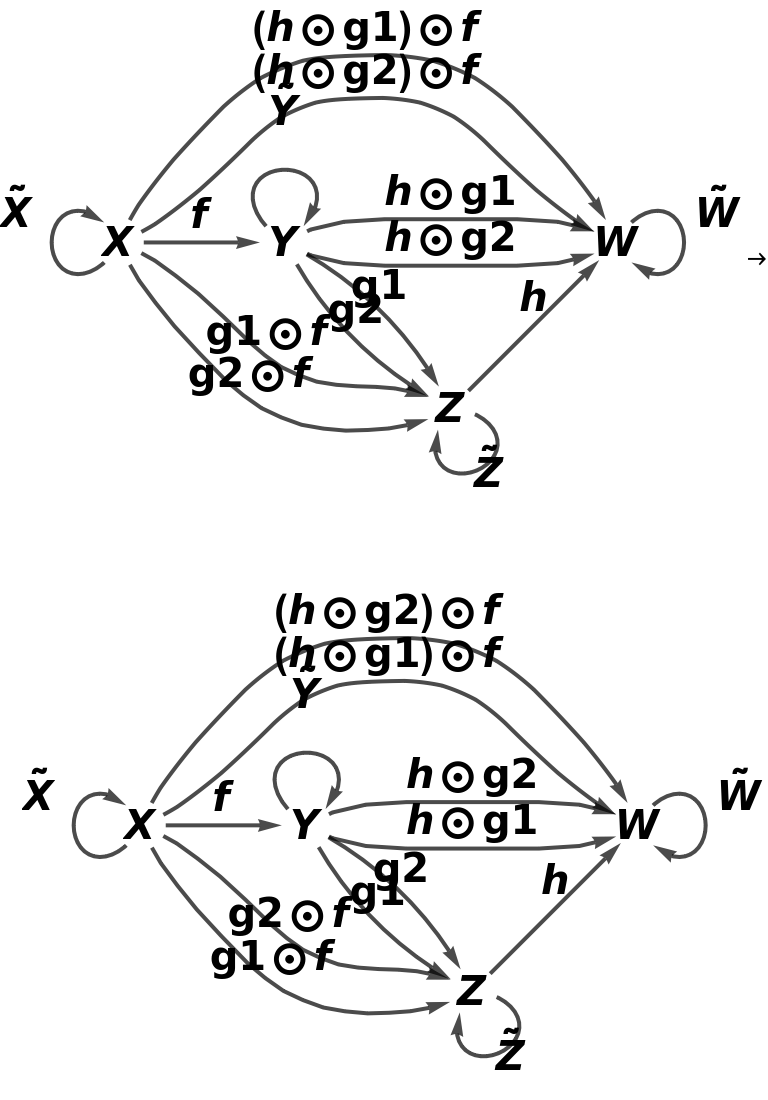
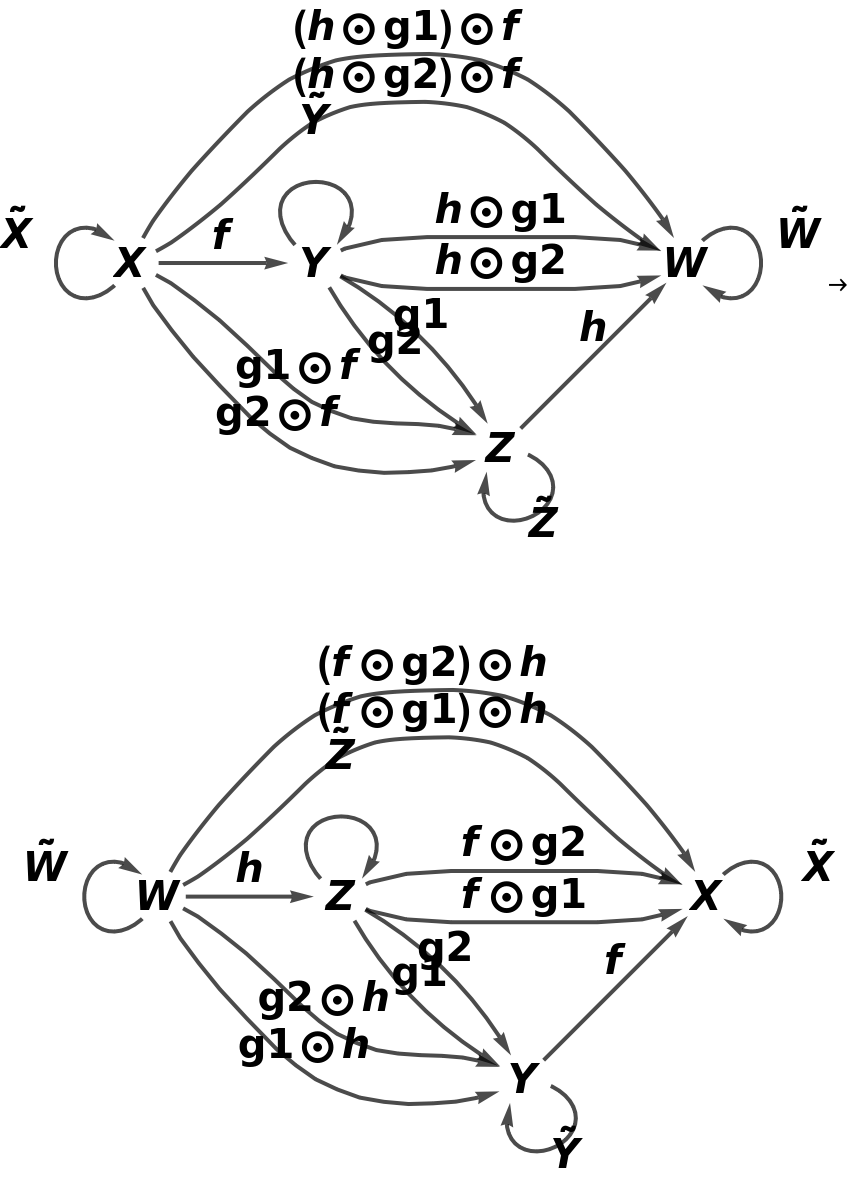
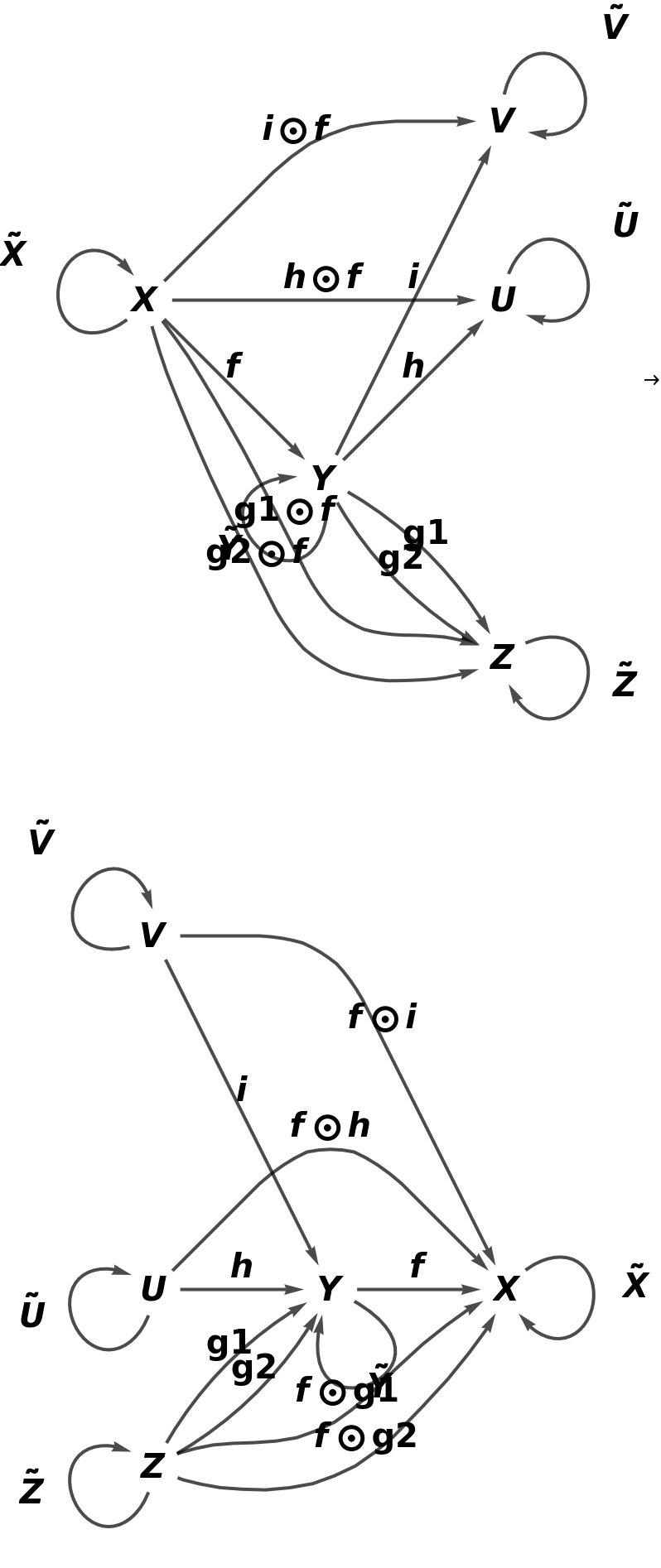
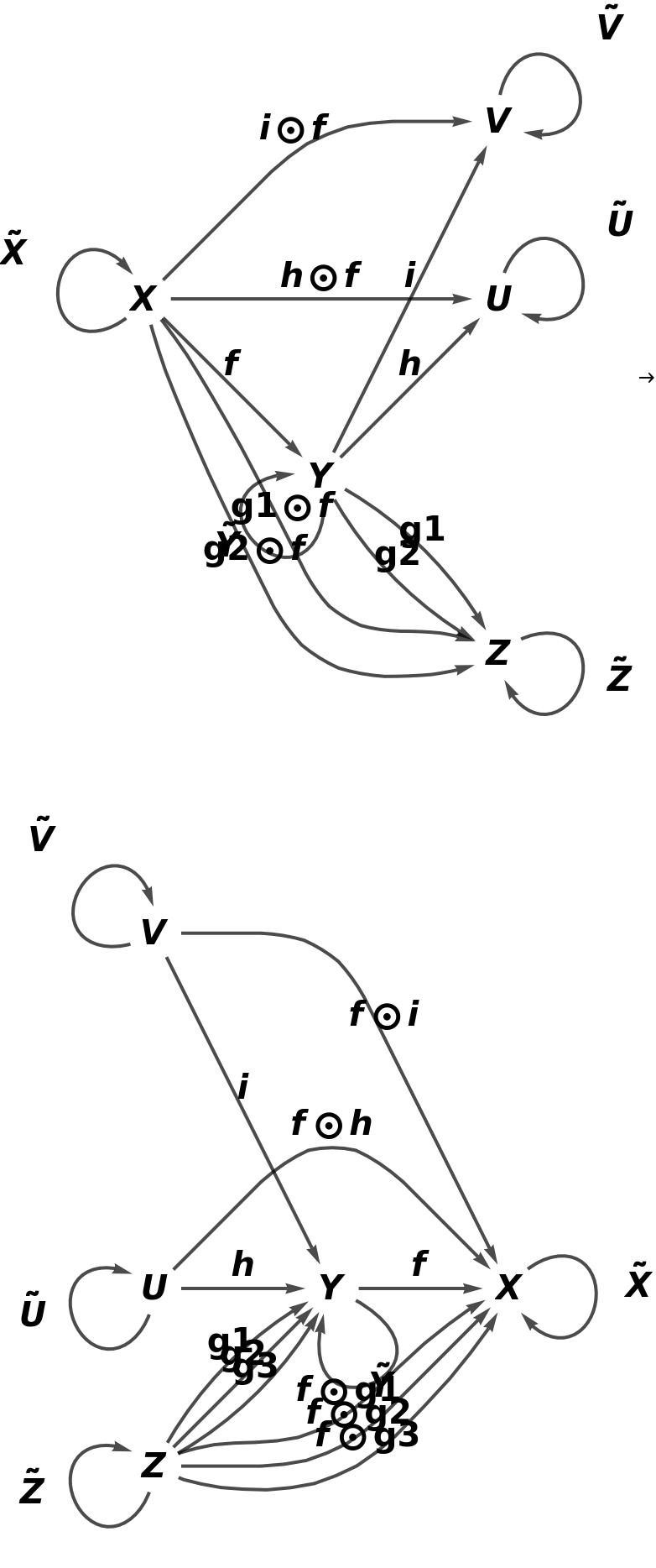
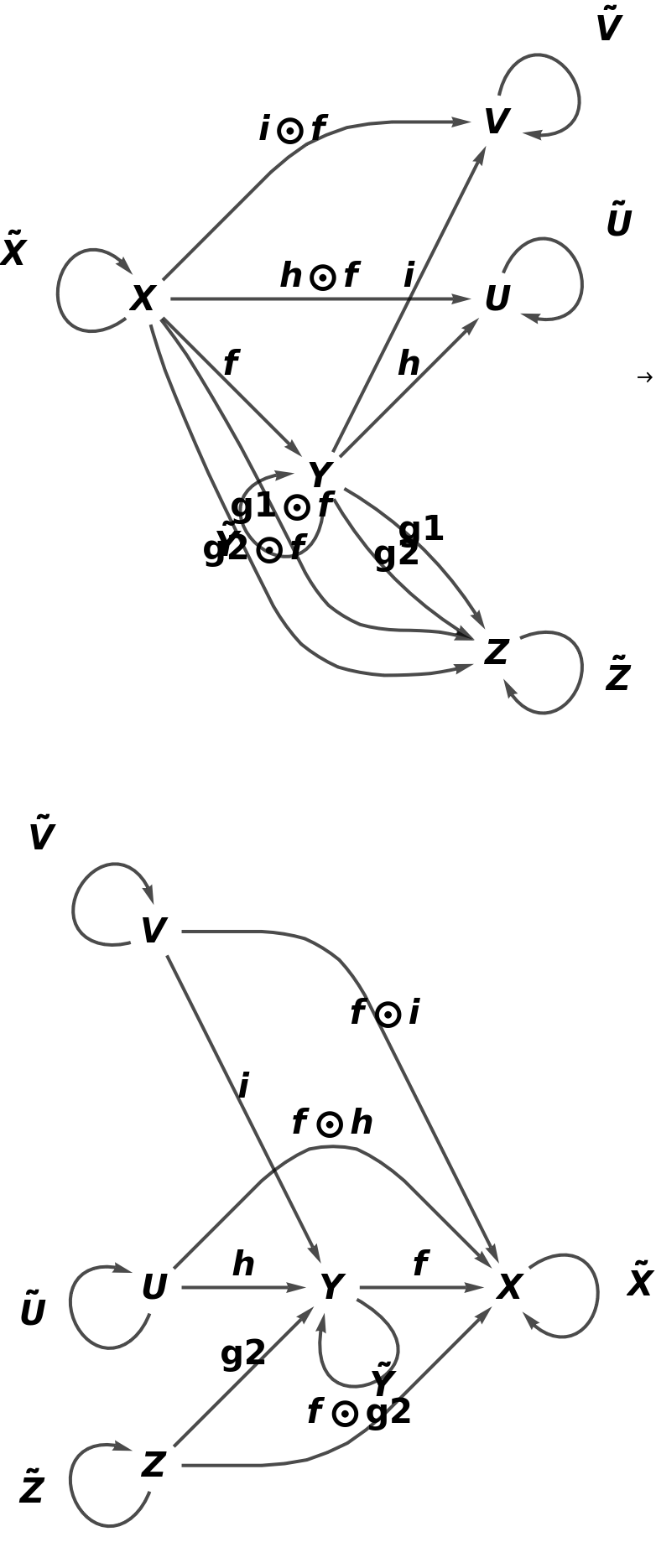
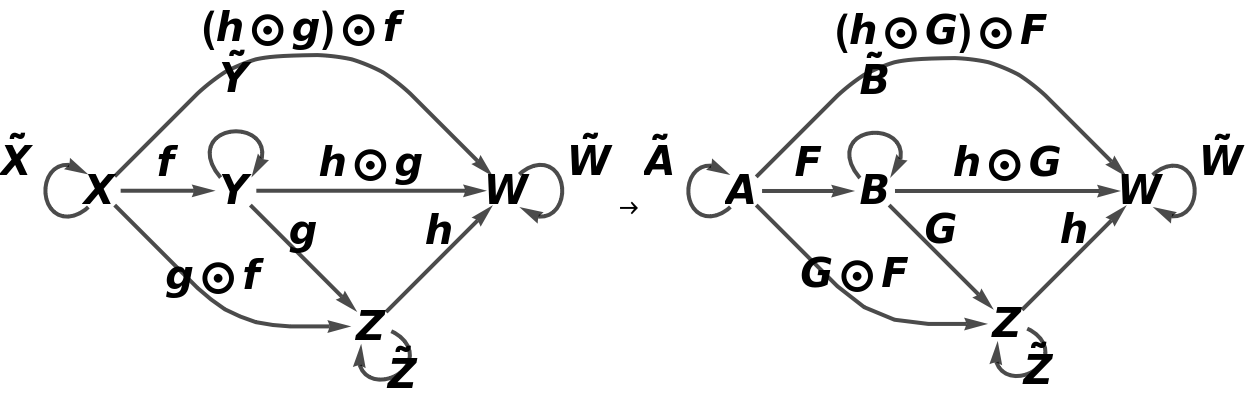
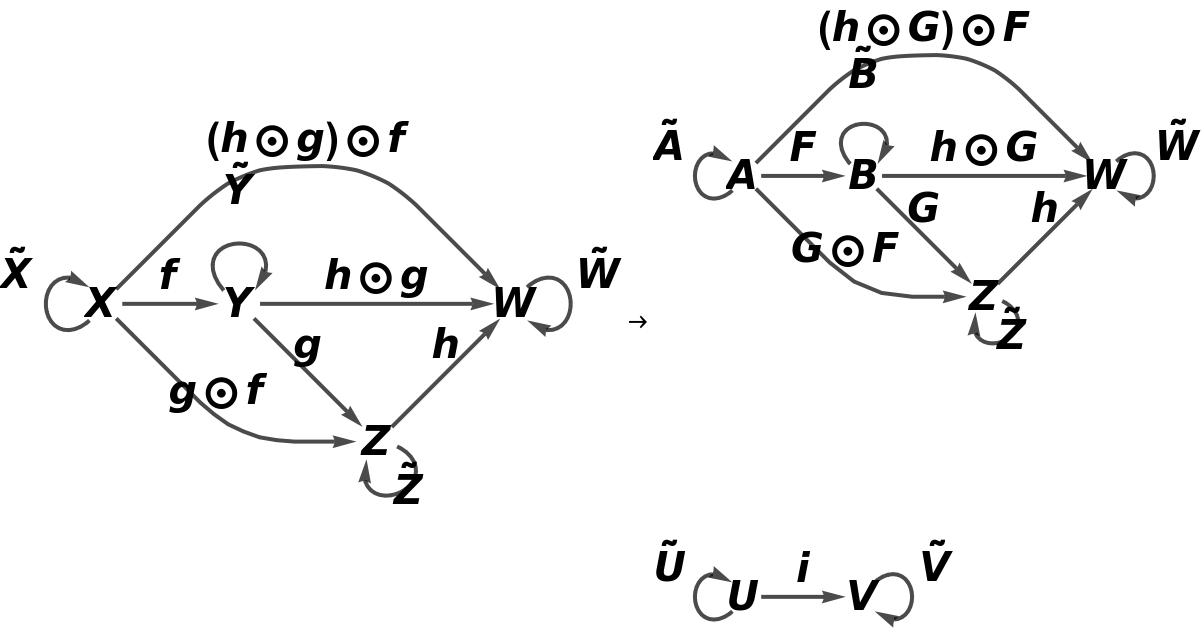
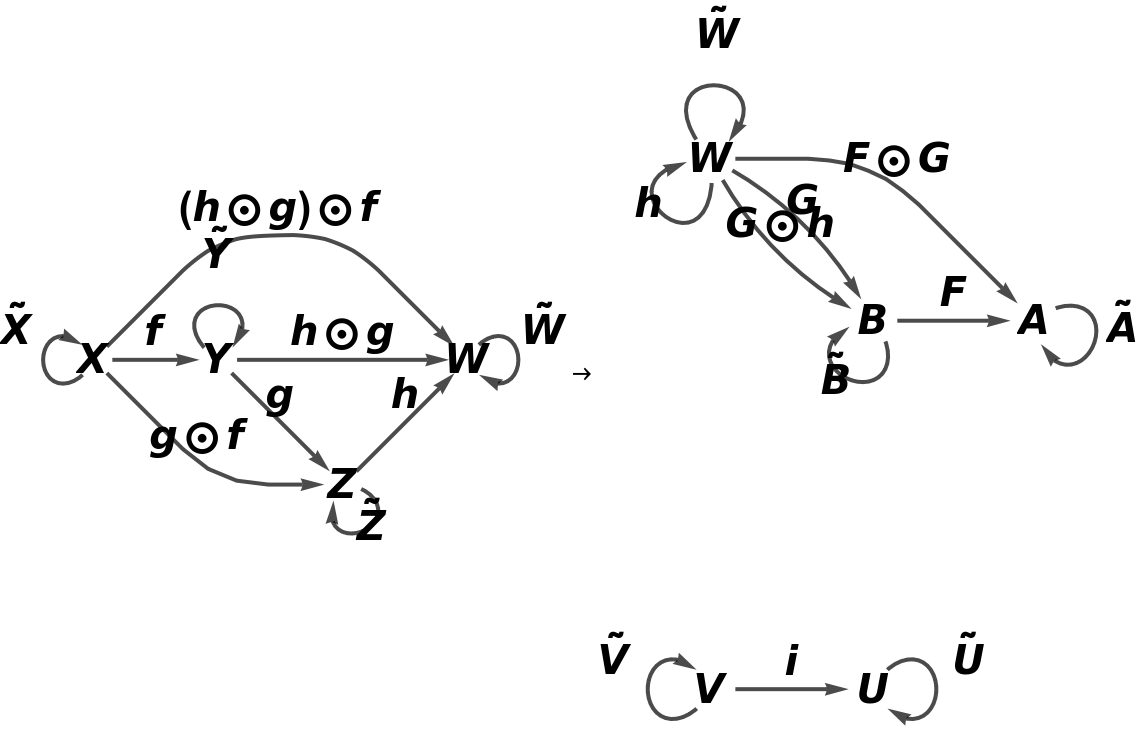
Show the full directed graphs with labels on the morphisms:
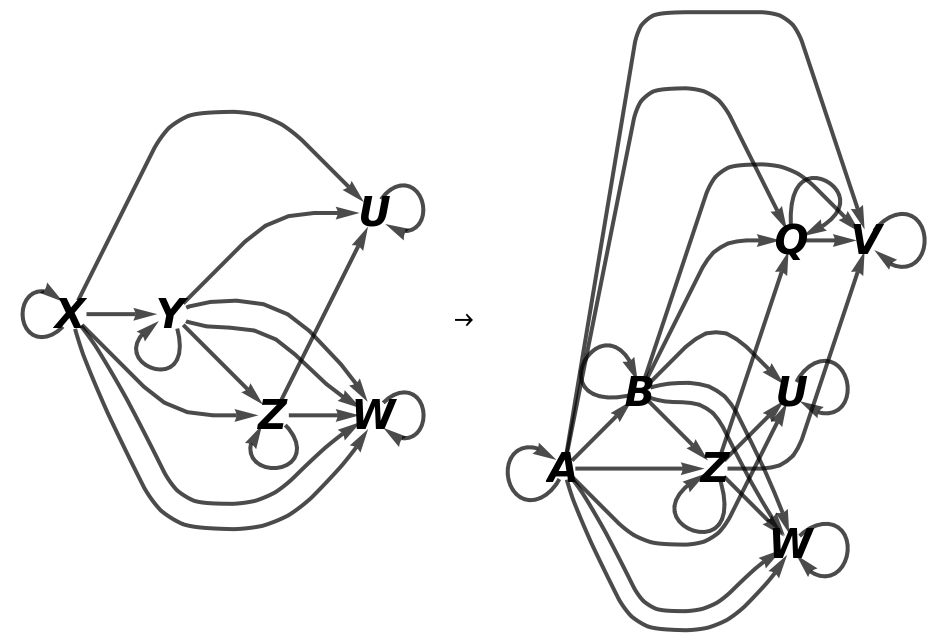
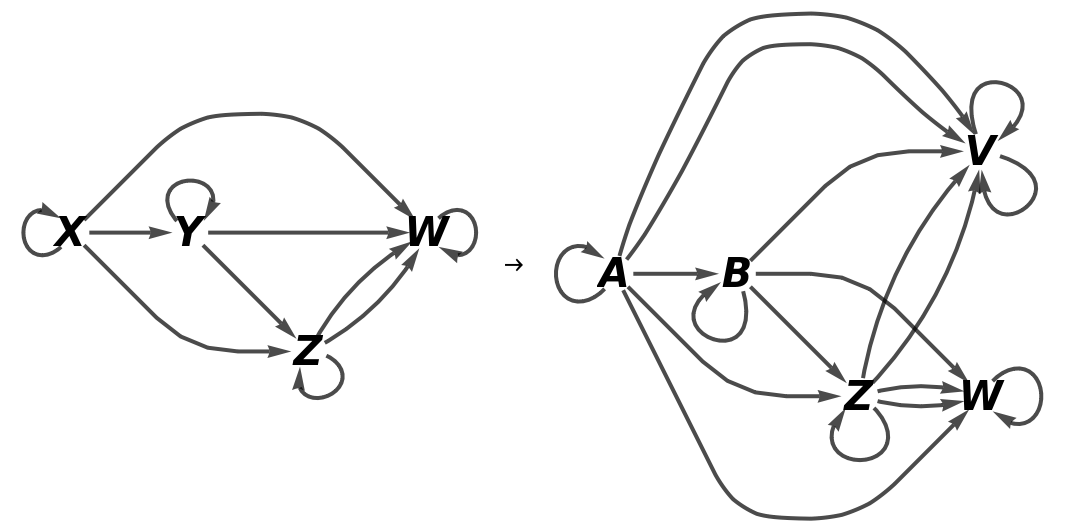
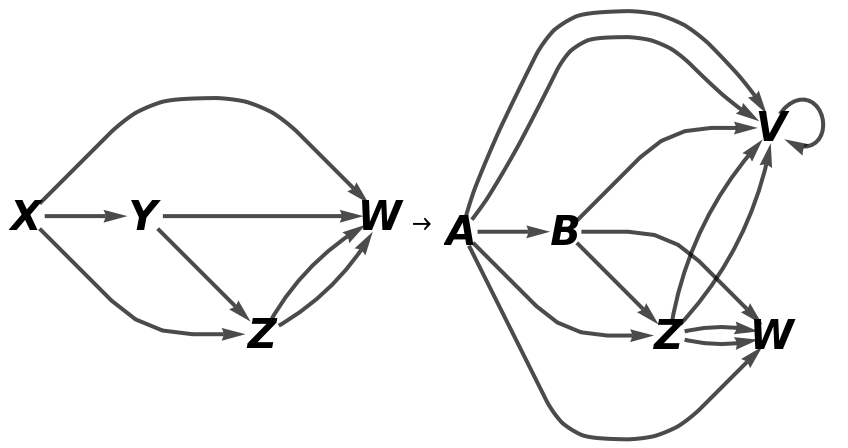
Show the full directed graphs without labels on the morphisms:
Show the association of object mappings:
Show the association of morphism mappings:
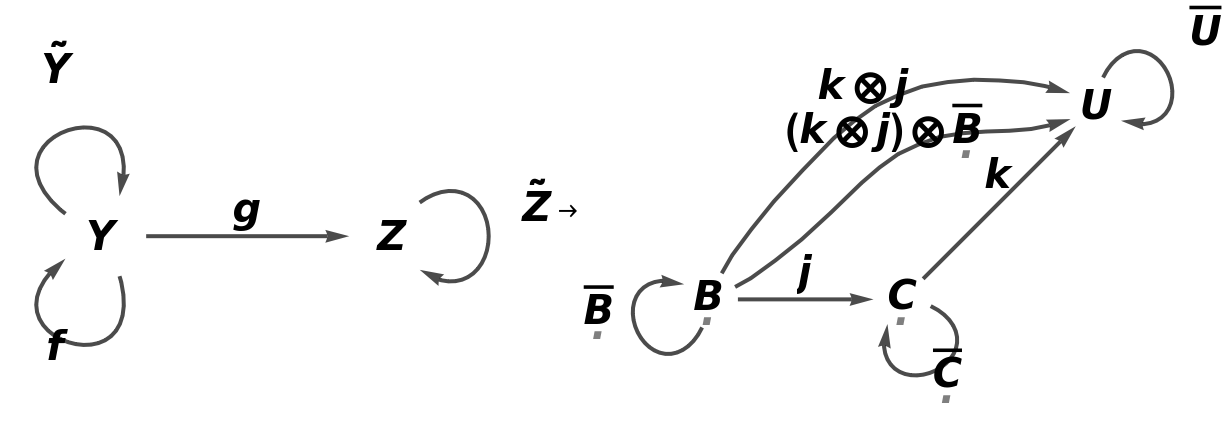
Construct the same abstract category, but now with an equivalence imposed between objects X and Y and morphisms g⊙f and g:
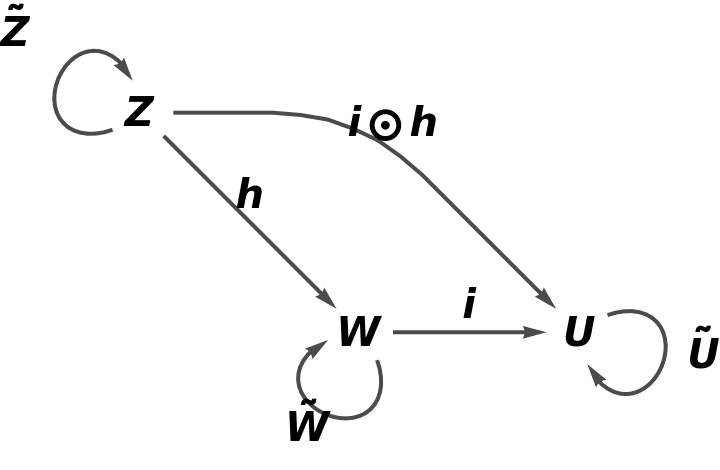
Construct an abstract functor from this new abstract category, with a new object U, with a new arrow k between objects C and U, with new composition and identity symbols ⊗ and ─, and with an equivalence imposed between morphisms i and  :
:
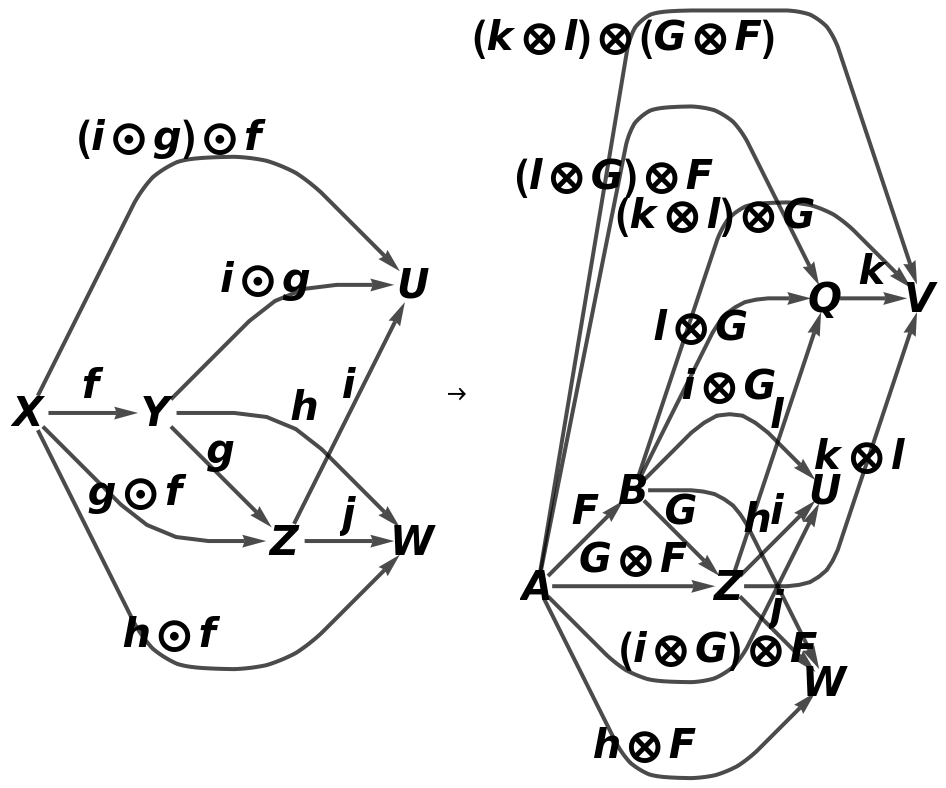
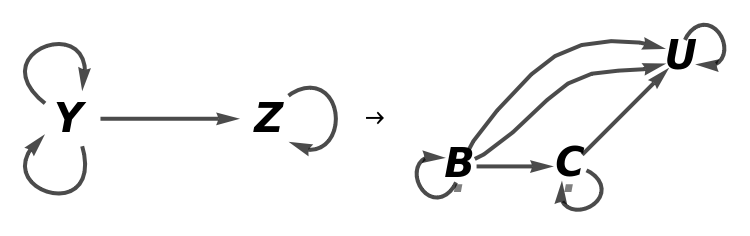
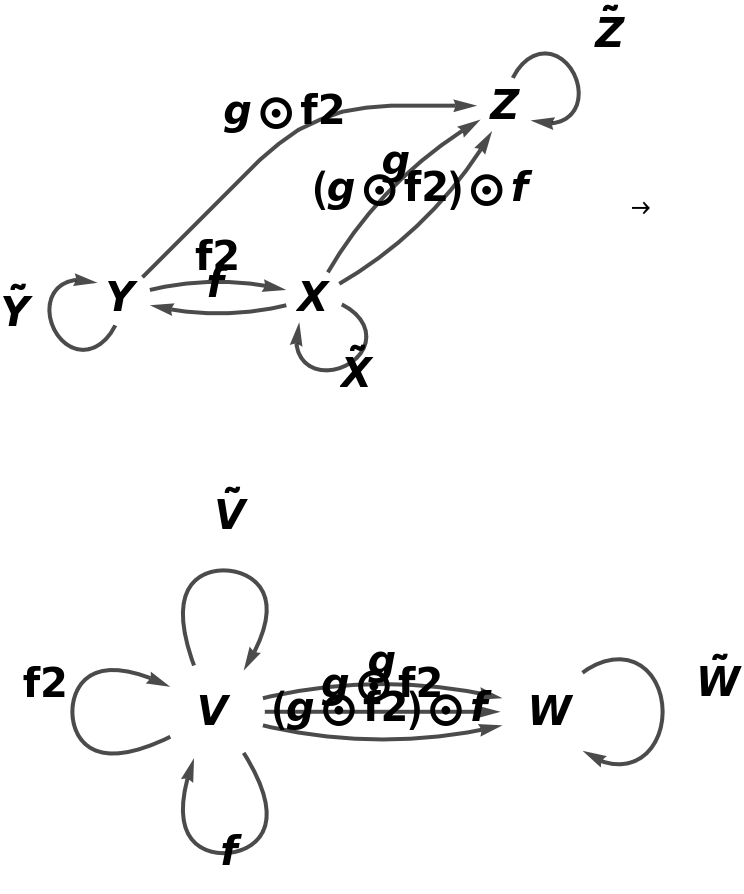
Show the reduced directed graphs, with all equivalences between objects and morphisms imposed and with labels on the morphisms:
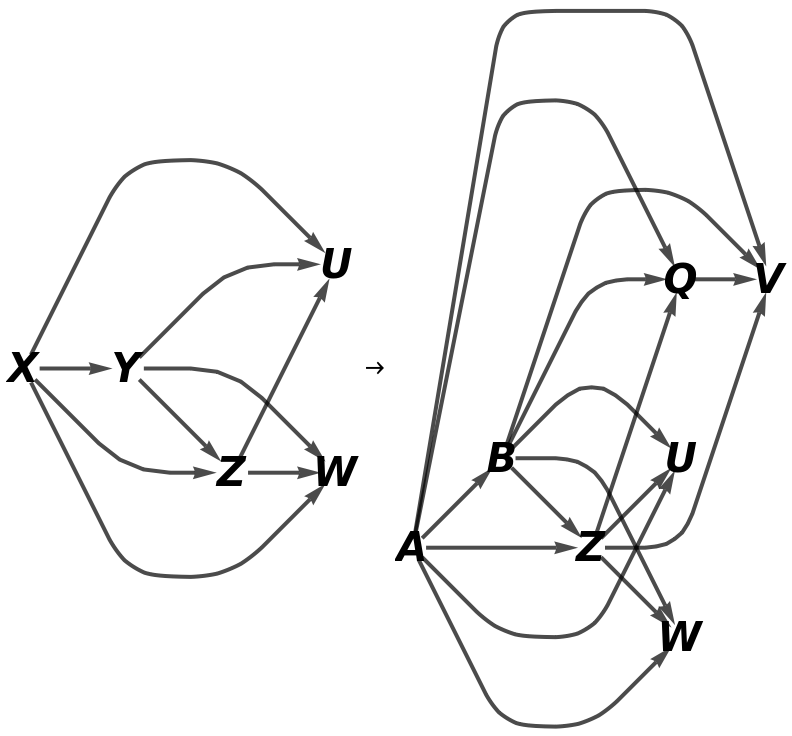
Show the reduced directed graphs without labels on the morphisms:
Show the association of object mappings, with all equivalences between objects imposed:
Show the association of morphism mappings, with all equivalences between objects and morphisms imposed:
Show the list of equivalences between objects:
Show the list of equivalences between morphisms:
Show the domain and codomain categories:
Show the association form of the abstract functor:
Construct an abstract functor from a simple abstract category to itself that swaps two of the arrows (g1 and g2) around:
Show that the functor is an endofunctor (a functor from a category to itself):
Show that the functor is not an identity functor (it does not map every object to itself and every morphism to itself):
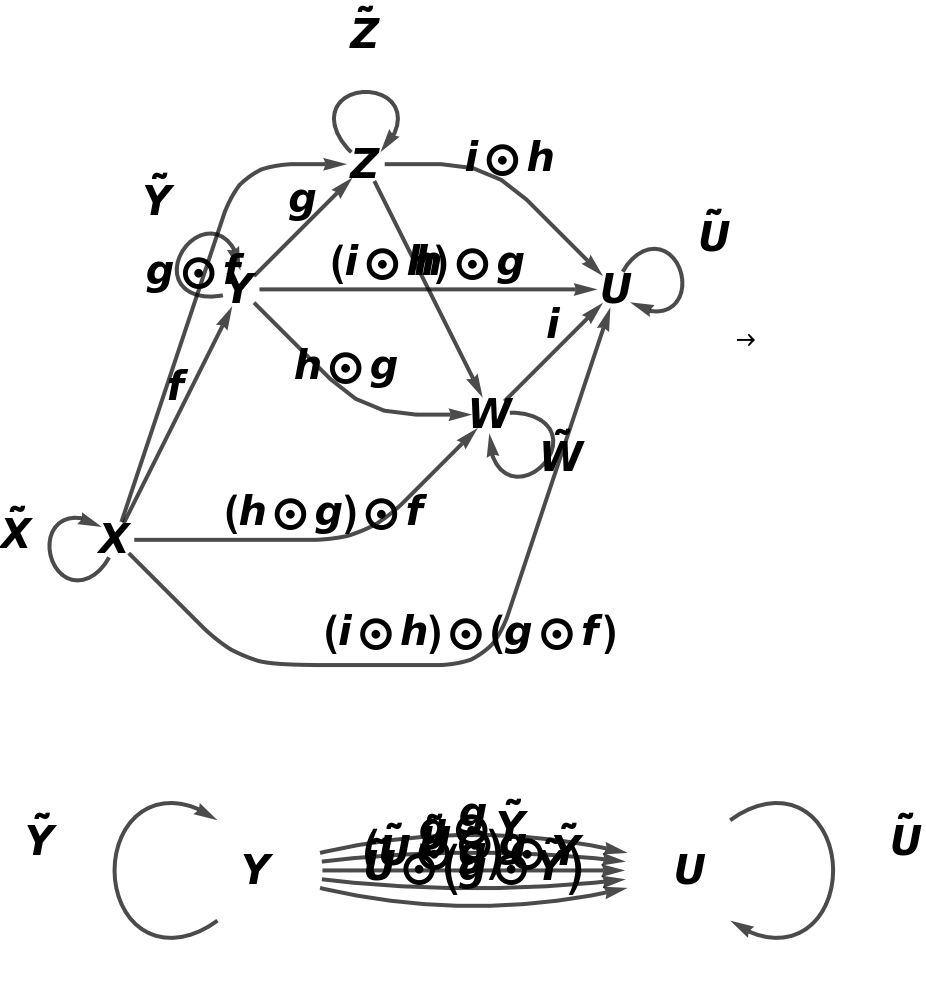
Return a contravariant version of the same abstract functor (in which the sources and targets of morphisms are swapped):
Show that the direction of morphism composition is reversed:
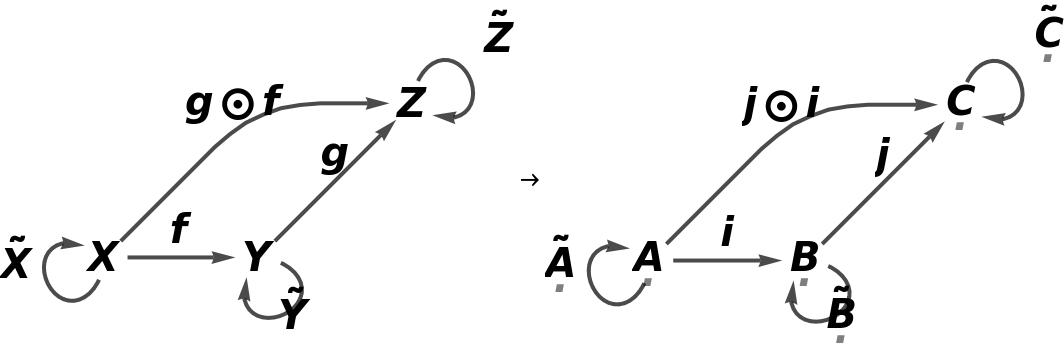
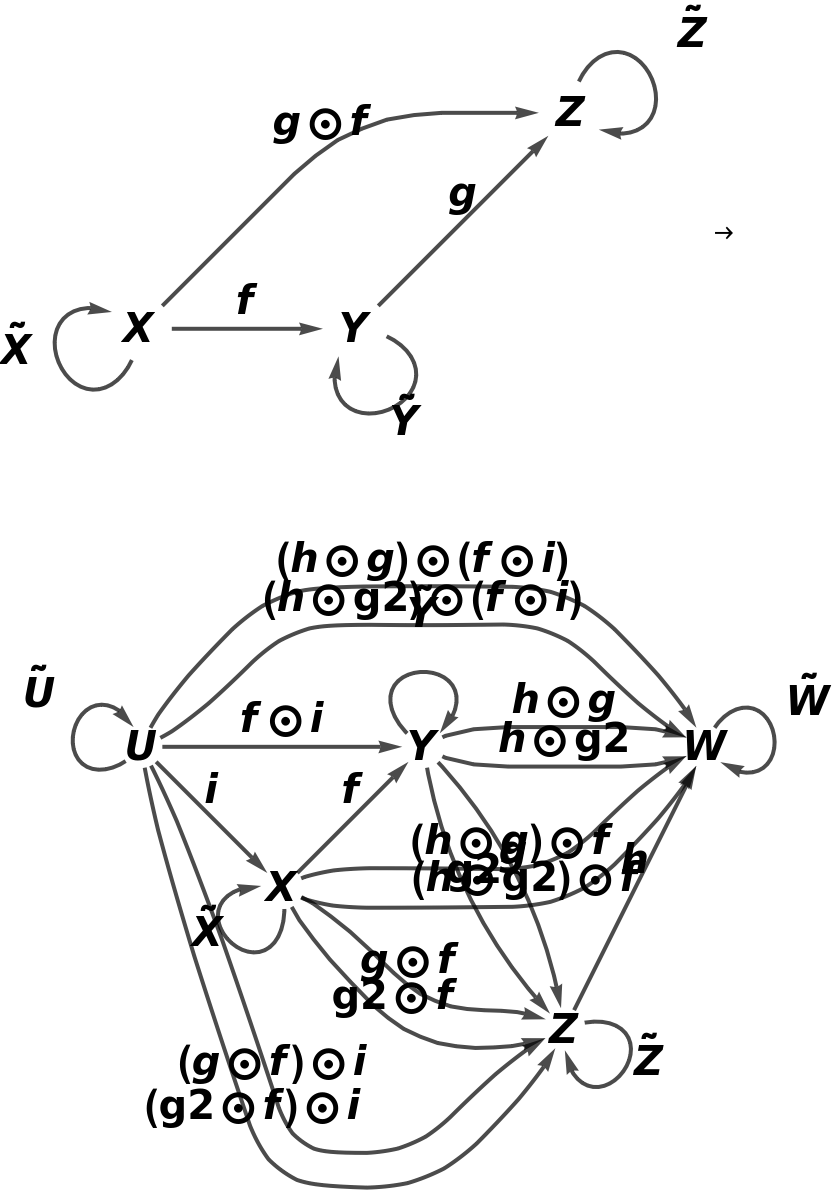
Construct a contravariant identity functor on a more complicated abstract category:
Show that the functor is both an endofunctor and an identity functor:
Show that the functor is full, faithful and fully faithful (i.e. it is surjective, injective and therefore bijective as a function on sets of morphisms between pairs of objects):
Construct a new contravariant functor that creates a new arrow (g3) between objects Z and Y:
Show the association of new morphisms:
Show that the functor is no longer full nor fully faithful, though it is still faithful (since it is now an injective, though not surjective, function on sets of morphisms between pairs of objects):
Construct a new contravariant functor that imposes an equivalence between morphisms g1 and g2 in the codomain category:
Show that the functor is no longer faithful nor fully faithful, though it is still full (since it is now a surjective, though not injective, function on sets of morphisms between pairs of objects):
Construct a simple abstract functor from an abstract category representing a span of (mono)morphisms:
Show that this functor is injective, surjective and bijective as a function on the sets of objects:
Construct a new abstract functor that introduces new objects X and Y:
Show that the functor is no longer surjective nor bijective as a function on the sets of objects, though it is still injective:
Show that by introducing isomorphisms between objects X and W and objects Y and V in the codomain category, the functor can nevertheless be made essentially surjective on objects:
Even though it is still not strictly surjective on objects:
Likewise, we can construct a new functor that imposes an equivalence between objects U and V in the codomain category:
Show that the functor is no longer injective nor bijective as a function on the sets of objects, though it is still surjective:
Show that by introducing an isomorphism between objects X and Y in the domain category, the functor can nevertheless be made essentially injective on objects:
Even though it is still not strictly injective on objects:
Show the list of equivalences between morphisms:
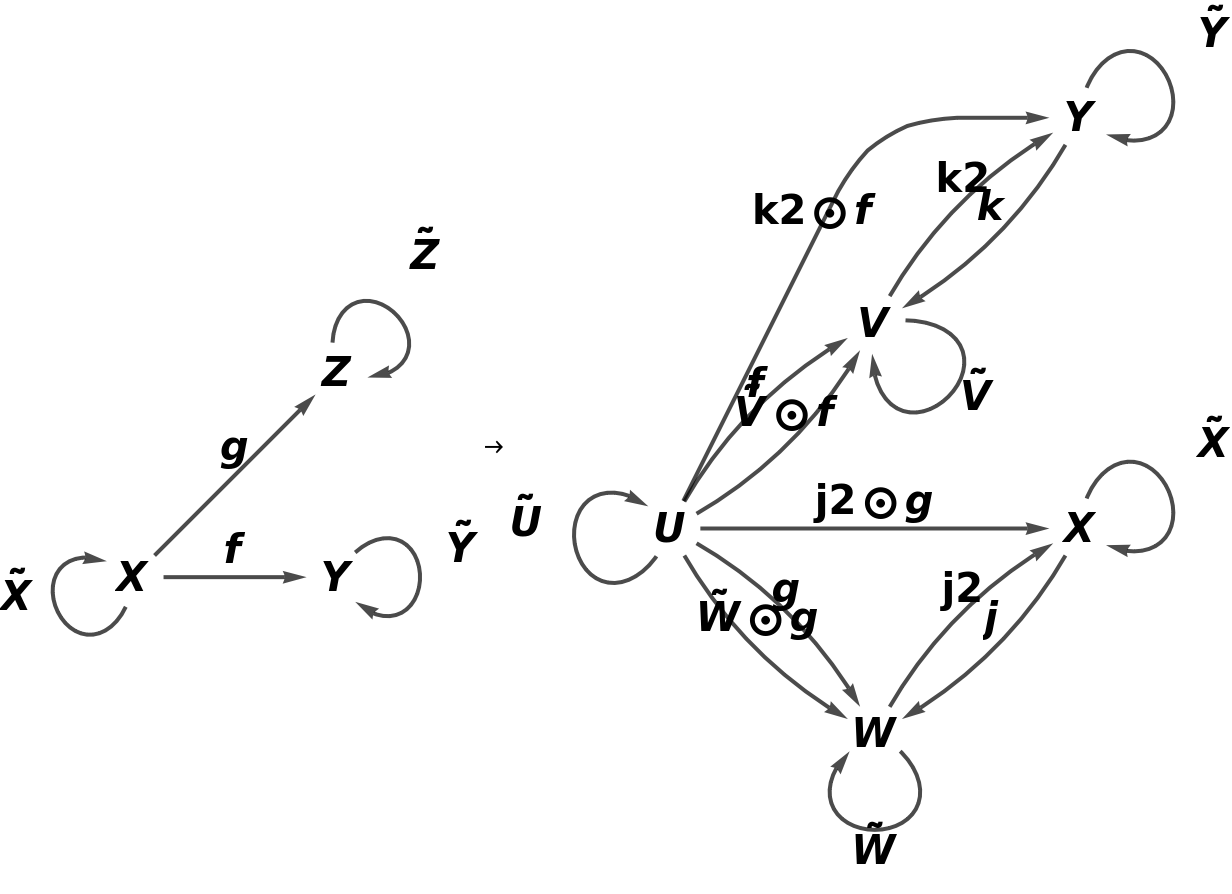
Construct an abstract functor that adds two new objects (W and U) and three new arrows (h, i and g2) to a simple abstract category:
Show that the functor is an inclusion functor (i.e. the domain is a subcategory of the codomain), but not a full inclusion functor (since it is not a full functor):
Similarly, show that the functor is an embedding functor (i.e. it is both faithful and injective on objects), but not a full embedding functor (i.e. it is not fully faithful and injective on objects):
Show that the functor does not yield an equivalence of categories (i.e. it is not fully faithful and essentially surjective):
Apply the abstract functor to the original abstract category (thus yielding the codomain category):
Apply the abstract functor to a larger abstract category (in which case it acts as an abstract functor on the relevant subcategory):
Construct an abstract functor that projects certain collections of objects in the domain category to single objects in the codomain category, and certain collections of morphisms in the domain category to identity morphisms in the codomain category (i.e. a simple fibration):
Show the association of fibers/fiber categories for each object in codomain category (i.e. show, for each object in the codomain category, which objects/morphisms in the domain category map to that object/its identity morphism in the codomain category):
Show the association of fibers/fiber categories for each object in the codomain category, with all equivalences between objects and morphisms imposed:
Show the graph form of the fiber associated to the object U in the codomain category:
Show that the fibration is not discrete:
Show that the functor is not constant (i.e. it does not map all objects in the domain category to a single object in the codomain category, and all morphisms in the domain category to the identity morphism on that object in the codomain category):
Show that the functor is nevertheless conservative (i.e. a morphism in the codomain category being an isomorphism necessarily implies that the corresponding morphism in the domain category is an isomorphism):
Show the association of morphism mappings, with all equivalences between objects and morphisms imposed:
Scope (3)
Abstract functors can be constructed directly by applying a function symbol (e.g. F) to an abstract category object:
If AbstractFunctor is given only an abstract category object, then its default behavior is to construct an identity functor on that category:
Additional arguments can be used to specify object and arrow mappings:
Further arguments can be used to specify new objects and new arrows that are introduced by the functor:
Further arguments can be used to specify new composition and identity symbols for the codomain category:
Further arguments can finally be used to specify new equivalences between objects and morphisms in the codomain category:
If the new composition and identity symbols are omitted, they are assumed to be the same as for the domain category:
New composition and identity symbols can be specified for any existing abstract functor:
Likewise for new object and morphism equivalences:
All four properties (new composition symbol, new identity symbol, new object equivalences and new morphism equivalences) may be specified simultaneously:
The optional first argument to AbstractFunctor specifies whether the functor is covariant (True) or contravariant (False):
From an explicit association:
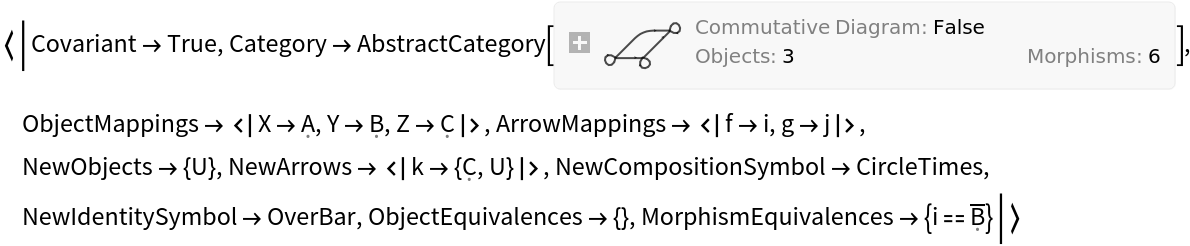
Construct an abstract functor from an abstract category and an association of object/arrow mappings, lists/associations of new objects/arrows, new composition/identity symbols and lists of new object/morphism equivalences:
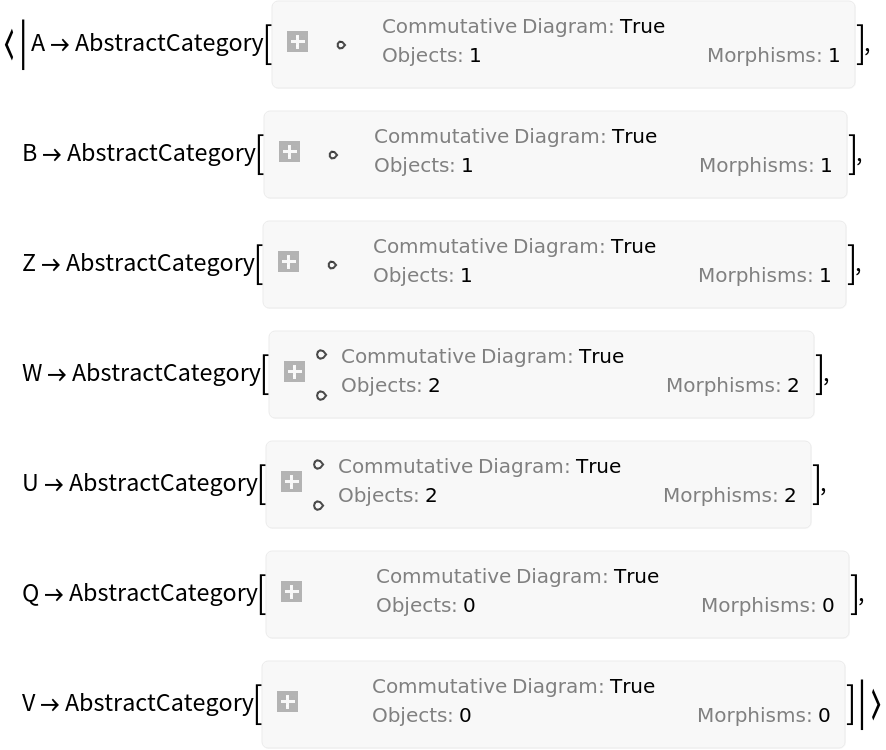
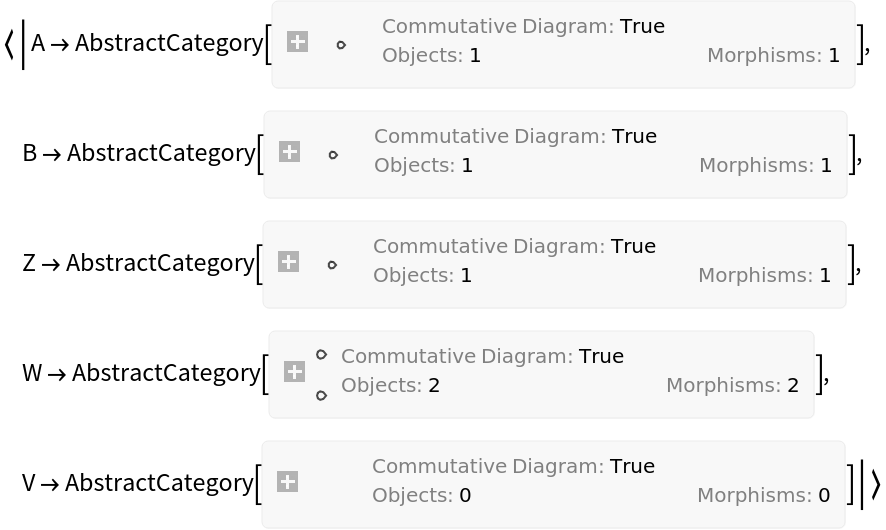
Show the list of properties:
Show the number of objects in the domain category vs. the codomain category of the abstract functor:
Show the number of morphisms in the domain category vs. the codomain category of the abstract functor:
Show the list of equivalences between objects in the codomain category of the abstract functor:
Show the number of equivalences between objects in the codomain category of the abstract functor:
Show the list of equivalences between morphisms in the codomain category of the abstract functor:
Show the number of equivalences between morphisms in the codomain category of the abstract functor:
Show the number of reduced objects (modded out by all object equivalences) in the domain category vs. the codomain category of the abstract functor:
Show the number of reduced morphisms (modded out by all object and morphism equivalences) in the domain category vs. the codomain category of the abstract functor:
Show the (binary) symbol used to denote morphism composition in the domain category vs. the codomain category of the abstract functor:
Show the (unary) symbol used to denote identity morphisms on objects in the domain category vs. the codomain category of the abstract functor:
Show the list of new objects in the codomain category that have no counterpart in the domain category of the abstract functor:
Show the number of new objects in the codomain category that have no counterpart in the domain category of the abstract functor:
Show the reduced list of new objects (modded out by all object equivalences) in the codomain category that have no counterpart in the domain category of the abstract functor:
Show the number of reduced new objects (modded out by all object equivalences) in the codomain category that have no counterpart in the domain category of the abstract functor:
Show the association of new morphisms in the codomain category that have no counterpart in the domain category of the abstract functor:
Show the number of new morphisms in the codomain category that have no counterpart in the domain category of the abstract functor:
Show the reduced association of new morphisms (modded out by all object and morphism equivalences) in the codomain category that have no counterpart in the domain category of the abstract functor:
Show the number of reduced new morphisms (modded out by all object and morphism equivalences) in the codomain category that have no counterpart in the domain category of the abstract functor:
Show the association of mappings between objects in the domain category and corresponding objects in the codomain category of the abstract functor:
Show the number of mappings between objects in the domain category and corresponding objects in the codomain category of the abstract functor:
Show the reduced association of mappings (modded out by all object equivalences) between objects in the domain category and corresponding objects in the codomain category of the abstract functor:
Show the number of reduced mappings (modded out by all object equivalences) between objects in the domain category and corresponding objects in the codomain category of the abstract functor:
Show the association of mappings between arrows in the underlying quiver of the domain category and corresponding arrows in the underlying quiver of the codomain category of the abstract functor:
Show the number of mappings between arrows in the underlying quiver of the domain category and corresponding arrows in the underlying quiver of the codomain category of the abstract functor:
Show the association of mappings between morphisms in the domain category and corresponding morphisms in the codomain category of the abstract functor:
Show the number of mappings between morphisms in the domain category and corresponding morphisms in the codomain category of the abstract functor:
Show the reduced association of mappings (modded out by all object and morphism equivalences) between morphisms in the domain category and corresponding morphisms in the codomain category of the abstract functor:
Show the number of reduced mappings (modded out by all object and morphism equivalences) between morphisms in the domain category and corresponding morphisms in the codomain category of the abstract functor:
Show the domain of the abstract functor (represented as an abstract category):
Show the codomain of the abstract functor (represented as an abstract category):
Determine whether the abstract functor is an endofunctor (i.e. a functor from an abstract category to itself):
Determine whether the abstract functor is an identity functor (i.e. an endofunctor that maps every object and every morphism to itself):
Determine whether the abstract functor is a constant functor/selection functor (i.e. a functor mapping every object to some fixed object in the codomain category, and every morphism to the identity morphism on that fixed object):
Determine whether the abstract functor is a full functor (i.e. a surjective function mapping sets of morphisms between pairs of objects in the domain category to corresponding sets of morphisms between corresponding pairs of objects in the codomain category):
Determine whether the abstract functor is a faithful functor (i.e. an injective function mapping sets of morphism between pairs of objects in the domain category to corresponding sets of morphisms between corresponding pairs of objects in the codomain category):
Determine whether the abstract functor is a fully faithful functor (i.e. a bijective function mapping sets of morphisms between pairs of objects in the domain category to corresponding sets of morphisms between corresponding pairs of objects in the codomain category):
Determine whether the abstract functor is injective on objects (i.e. an injective function mapping the set of objects in the domain category to the corresponding set of objects in the codomain category):
Determine whether the abstract functor is an essentially injective functor (i.e. a function mapping the set of objects in the domain category to the corresponding set of objects in the codomain category that is injective up to isomorphism):
Determine whether the abstract functor is surjective on objects (i.e. a surjective function mapping the set of objects in the domain category to the corresponding set of objects in the codomain category):
Determine whether the abstract functor is an essentially surjective functor (i.e. a function mapping the set of objects in the domain category to the corresponding set of objects in the codomain category that is surjective up to isomorphism):
Determine whether the abstract functor is bijective on objects (i.e. a bijective function mapping the set of objects in the domain category to the corresponding set of objects in the codomain category):
Determine whether the abstract functor is an essentially bijective functor (i.e. a function mapping the set of objects in the domain category to the corresponding set of objects in the codomain category that is bijective up to isomorphism):
Determine whether the abstract functor is conservative (i.e. if a morphism in the codomain category is an isomorphism, then the corresponding morphism in the domain category is necessarily an isomorphism):
Determine whether the abstract functor yields an equivalence of categories (i.e. a functor that is fully faithful and essentially surjective):
Compute the association of fibers/fiber categories for each object in the codomain category of the abstract functor (i.e. the objects/morphisms in the domain category that project onto a given object/identity morphism in the codomain category):
Compute the association of fibers/fiber categories for each object in the codomain category of the abstract functor (i.e. the objects/morphisms in the domain category that project onto a given object/identity morphism in the codomain category), modded out by all object and morphism equivalences:
Determine whether the abstract functor corresponds to a discrete fibration (i.e. a special case of a Grothendieck fibration in which the fibers are discrete categories):
Determine whether the abstract functor corresponds to an inclusion functor for a subcategory (i.e. a functor for which the objects/morphisms in the domain category form a subset of the objects/morphisms in the codomain category):
Determine whether the abstract functor corresponds to a full inclusion functor for a subcategory (i.e. an inclusion functor that is also a full functor):
Determine whether the abstract functor is an embedding functor (i.e. a functor that is faithful and injective on objects):
Determine whether the abstract functor is a full embedding functor (i.e. a functor that is fully faithful and injective on objects):
Swap the variance of the abstract functor (i.e. return a contravariant version of the abstract functor if it was originally covariant, and likewise return a covariant version of the abstract functor if it was originally contravariant):
Determine whether the abstract functor is a covariant functor (i.e. a functor that preserves the source/target objects of morphisms and the direction of morphism composition):
Determine whether the abstract functor is a contravariant functor (i.e. a functor that swaps the source/target objects of morphisms and reverses the direction of morphism composition):
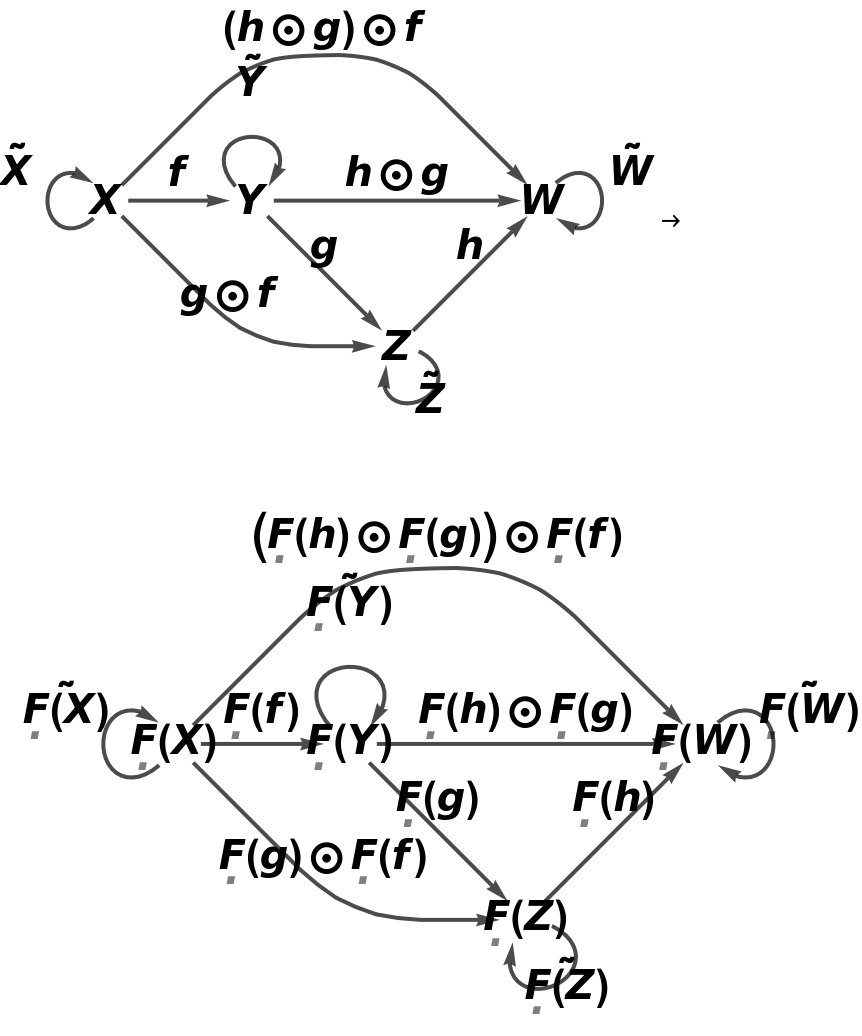
Show the abstract functor represented as a map between full directed graphs with labels on the morphisms:
Show the abstract functor represented as a map between full directed graphs without labels on the morphisms:
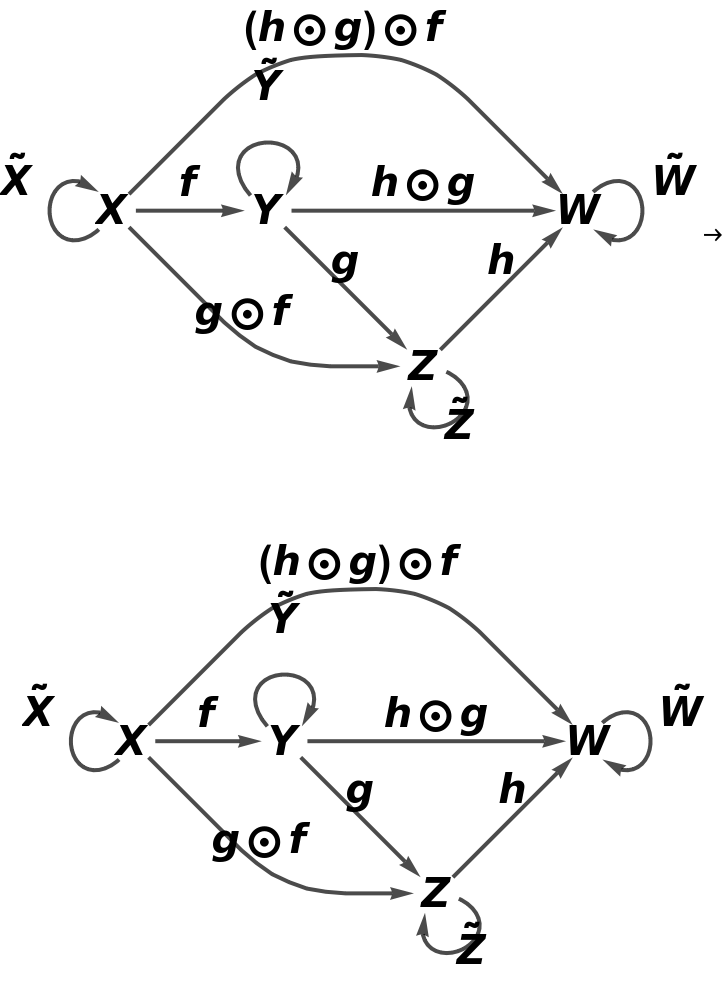
Show the abstract functor represented as a map between reduced directed graphs, with all equivalences between objects and morphisms imposed and with labels on the morphisms:
Show the abstract functor represented as a map between reduced directed graphs, with all equivalences between objects and morphisms imposed and without labels on the morphisms:
Show the abstract functor represented as a map between simple directed graphs, with all self-loops and multiedges removed and with labels on the morphisms:
Show the abstract functor represented as a map between simple directed graphs, with all self-loops and multiedges removed and without labels on the morphisms:
Show the abstract functor represented as a map between reduced simple directed graphs, with all self-loops and multiedges removed, plus all object and morphism equivalences modded out and with labels on the morphisms:
Show the abstract functor represented as a map between reduced simple directed graphs, with all self-loops and multiedges removed, plus all object and morphism equivalences modded out and without labels on the morphisms:
Show the explicit association form of the functor:
![]() :
:
![category = ResourceFunction["AbstractCategory"][<|f -> {X, Y}, g1 -> {Y, Z}, g2 -> {Y, Z}, h -> {Y, U}, i -> {Y, V}|>]](https://www.wolframcloud.com/obj/resourcesystem/images/b62/b62a62d8-81b0-454a-aea8-4bb718ddc82d/6c37fd6c4eea23fe.png)
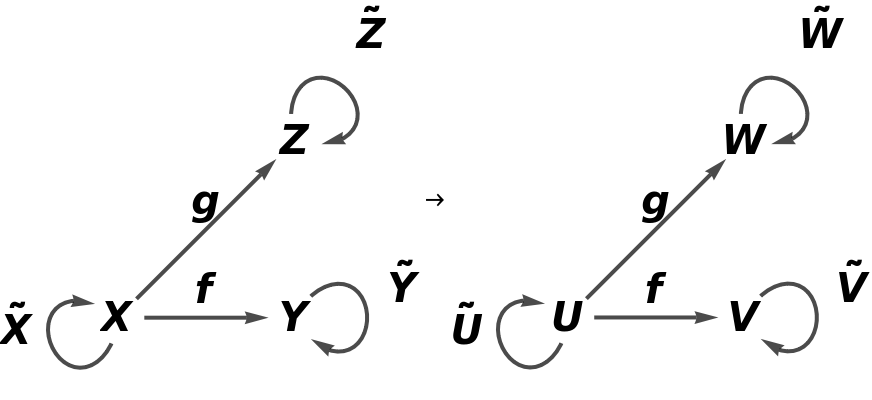
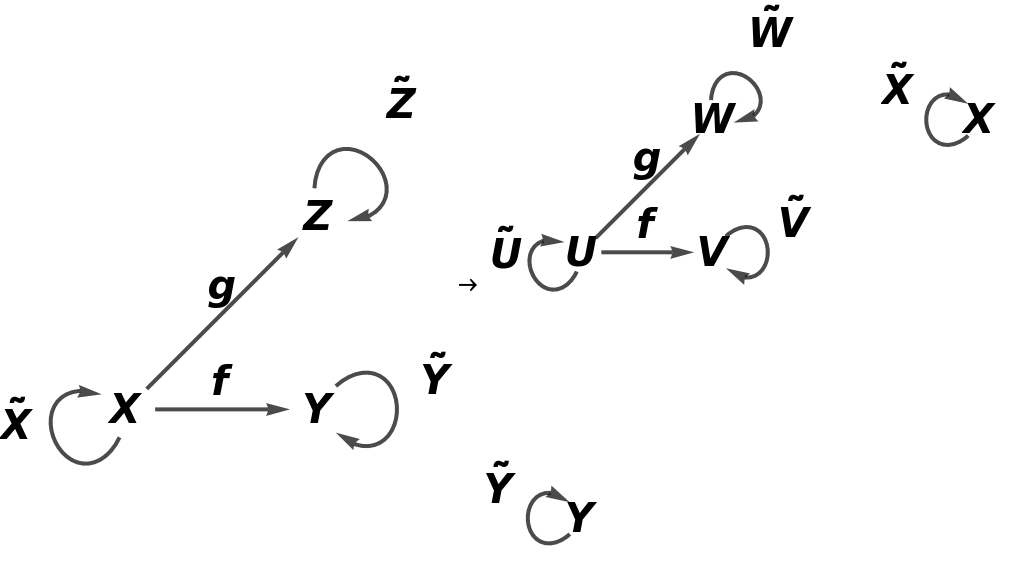
![functor3 = ResourceFunction["AbstractFunctor"][
category, <|X -> U, Y -> V, Z -> W|>, <||>, {X, Y}, <|j -> {X, W}, j2 -> {W, X}, k -> {Y, V}, k2 -> {V, Y}|>, {}, {CircleDot[j, j2] == OverTilde[W], CircleDot[j2, j] == OverTilde[X], CircleDot[k, k2] == OverTilde[V],
CircleDot[k2, k] == OverTilde[Y]}]](https://www.wolframcloud.com/obj/resourcesystem/images/b62/b62a62d8-81b0-454a-aea8-4bb718ddc82d/0833426bdf91b2d0.png)
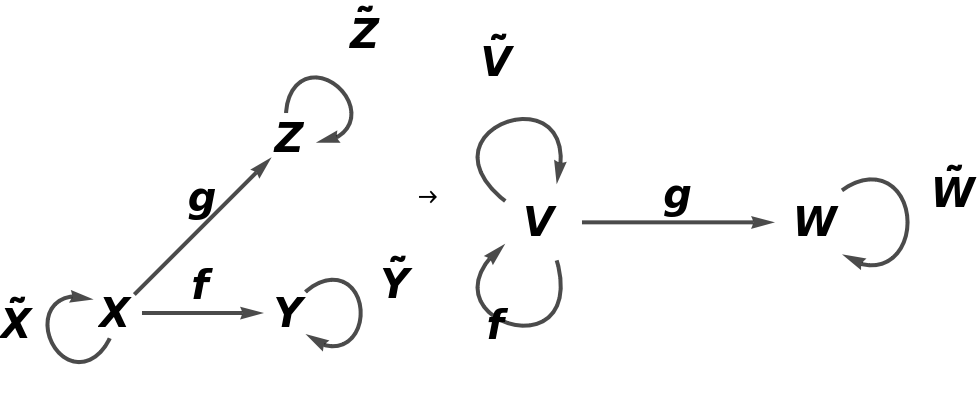
![functor = ResourceFunction["AbstractFunctor"][
category, <||>, <||>, {}, <||>, {X == Y, W == U, Z == W}, {i == OverTilde[U], f == OverTilde[Y], h == OverTilde[U], CircleDot[OverTilde[U], OverTilde[U]] == OverTilde[U]}]](https://www.wolframcloud.com/obj/resourcesystem/images/b62/b62a62d8-81b0-454a-aea8-4bb718ddc82d/054bf5037a4ace08.png)

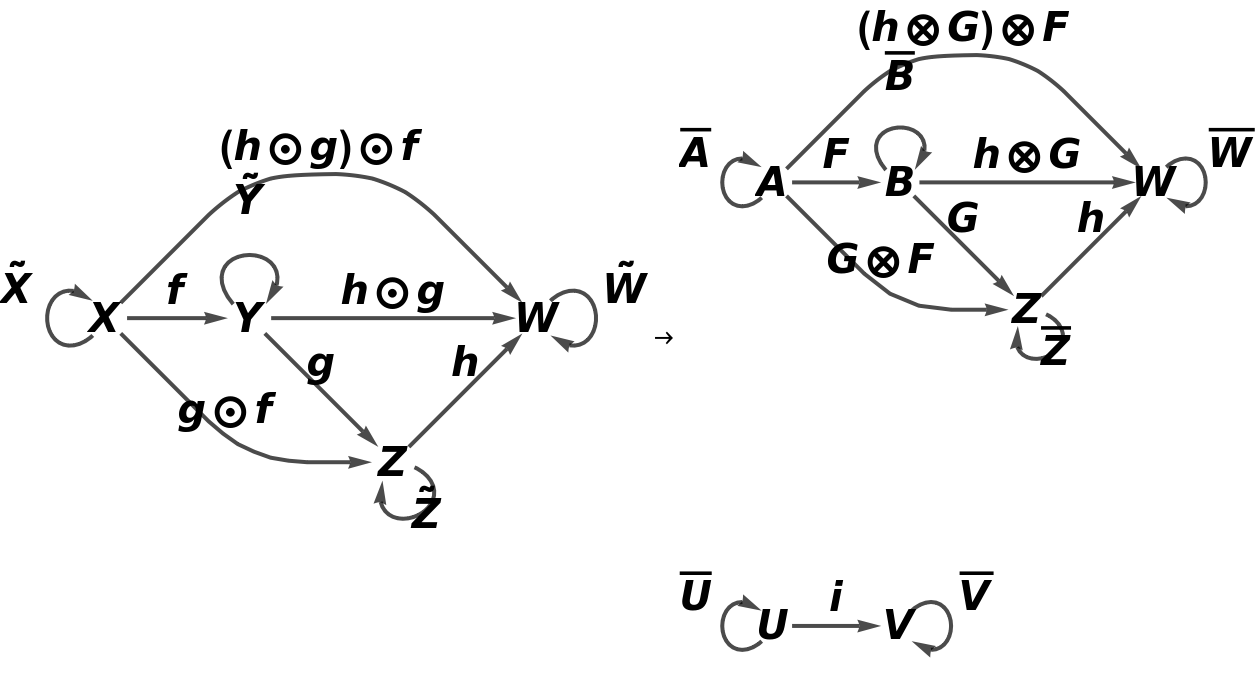
![functor5 = ResourceFunction["AbstractFunctor"][
category, <|X -> A, Y -> B|>, <|f -> F, g -> G|>, {U, V}, <|
i -> {U, V}|>, CircleTimes, OverBar, {Z == W}, {CircleTimes[G, F] == CircleTimes[CircleTimes[h, G], F]}]](https://www.wolframcloud.com/obj/resourcesystem/images/b62/b62a62d8-81b0-454a-aea8-4bb718ddc82d/24197c5b49105eb5.png)
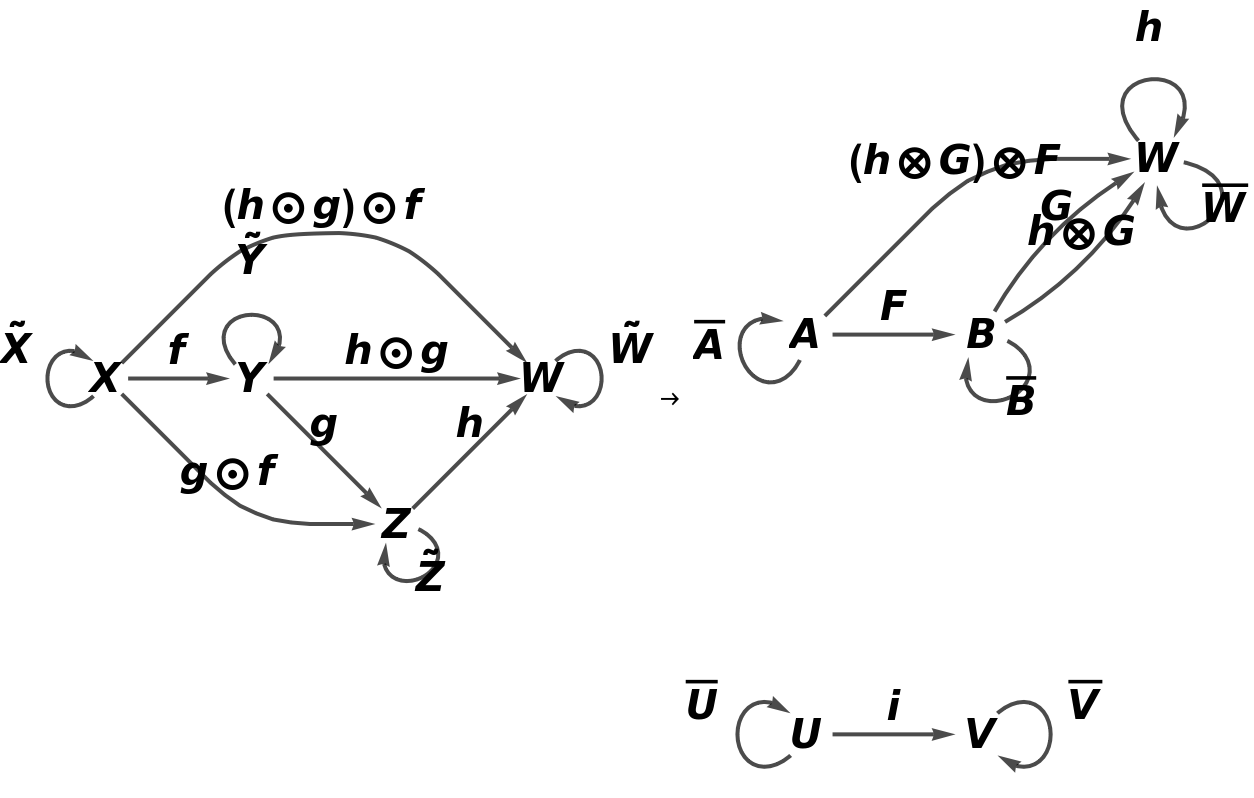
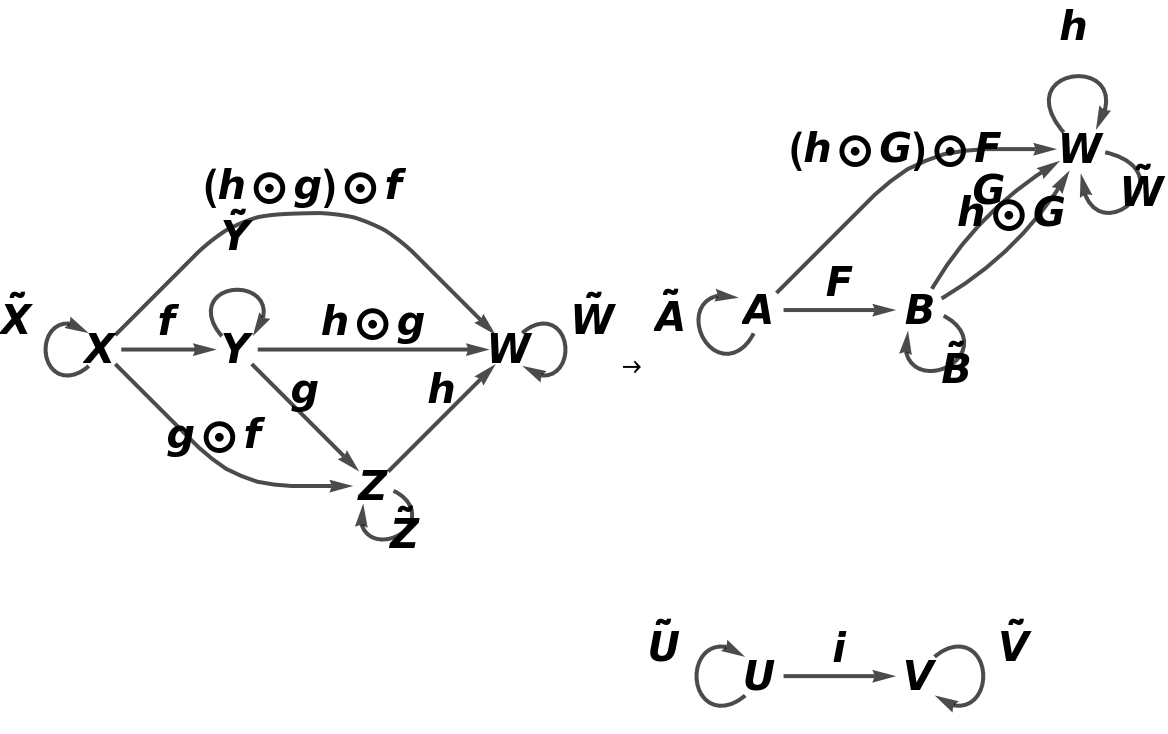
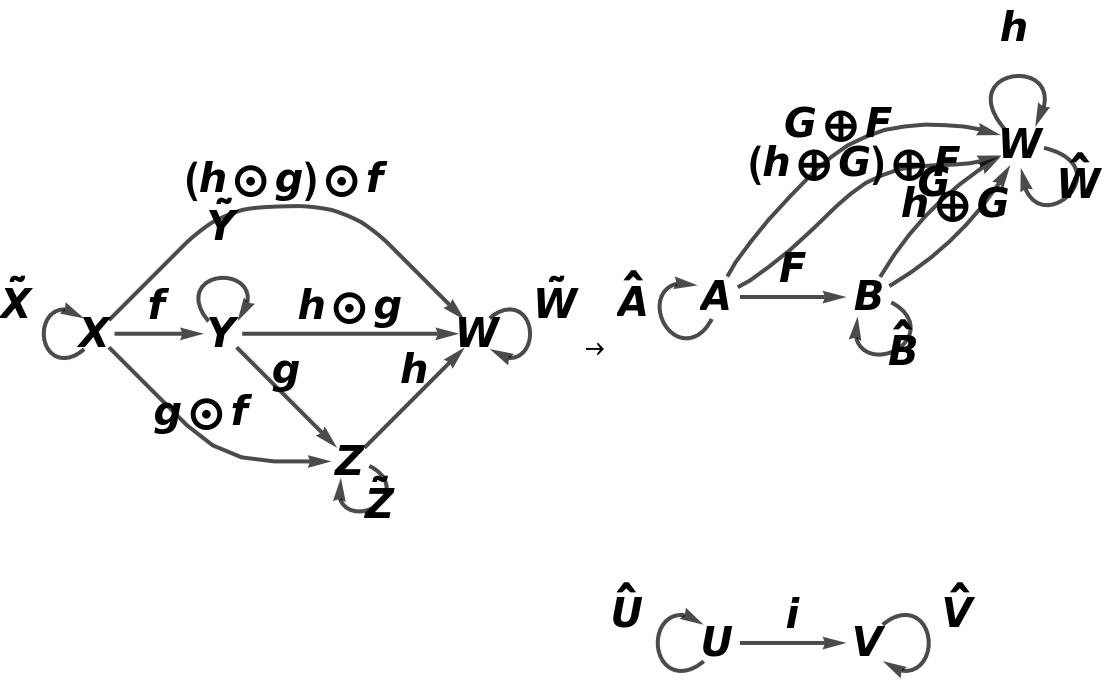
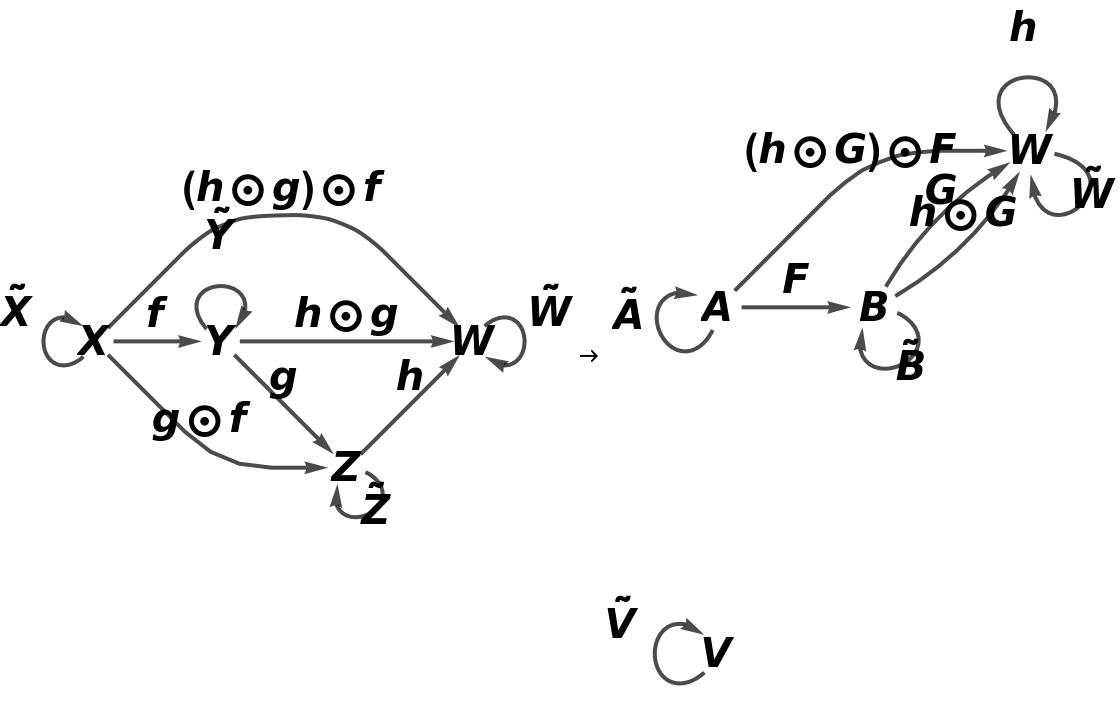
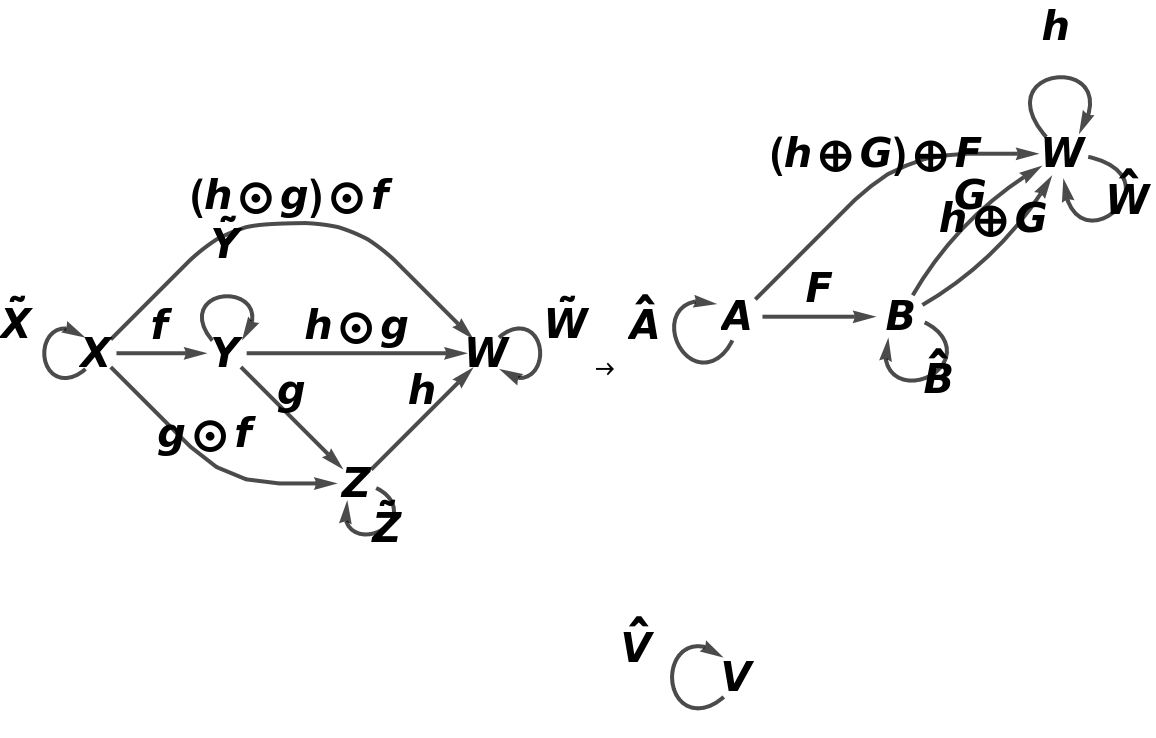
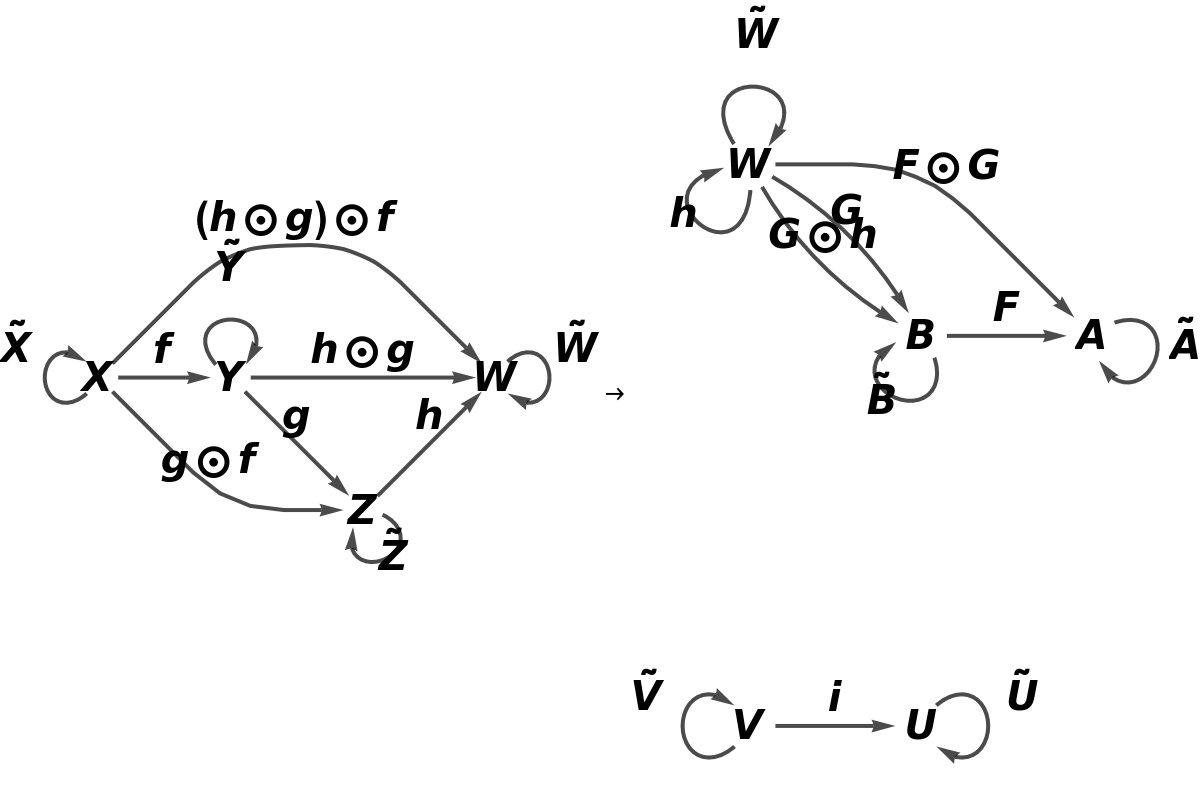
![functor11 = ResourceFunction[
"AbstractFunctor"][<|"Covariant" -> False, "Category" -> category, "ObjectMappings" -> <|X -> A, Y -> B|>, "ArrowMappings" -> <|f -> F, g -> G|>, "NewObjects" -> {U, V}, "NewArrows" -> <|i -> {V, U}|>, "NewCompositionSymbol" -> CircleDot, "NewIdentitySymbol" -> OverTilde, "ObjectEquivalences" -> {Z == W},
"MorphismEquivalences" -> {CircleDot[CircleDot[F, G], h] == CircleDot[F, G]}|>]](https://www.wolframcloud.com/obj/resourcesystem/images/b62/b62a62d8-81b0-454a-aea8-4bb718ddc82d/18bf620c0974d74c.png)
![category = ResourceFunction["AbstractCategory"][<|f -> {X, Y}, g -> {Y, Z}, h -> {Y, W}, i -> {Z, U}, j -> {Z, W}|>, {U == W}, {CircleDot[i, g] == h, CircleDot[j, g] == h}]](https://www.wolframcloud.com/obj/resourcesystem/images/b62/b62a62d8-81b0-454a-aea8-4bb718ddc82d/5483badf44f7a82b.png)
![functor = ResourceFunction["AbstractFunctor"][
category, <|X -> A, Y -> B|>, <|f -> F, g -> G|>, {Q, V}, <|
k -> {Q, V}, l -> {Z, Q}|>, CircleTimes, OverBar, {Q == V}, {CircleTimes[l, G] == CircleTimes[CircleTimes[k, l], G]}]](https://www.wolframcloud.com/obj/resourcesystem/images/b62/b62a62d8-81b0-454a-aea8-4bb718ddc82d/5c715f2b837b5dfc.png)