Function Repository Resource:

AberrancyCurve

Compute the curve of aberrancy of a plane curve

Contributed by: Jan Mangaldan

ResourceFunction["AberrancyCurve"][c,t]

computes the curve of aberrancy of the plane curve c parametrized by variable t.

Details

The curve of aberrancy is also known as the affine evolute.

The curve of aberrancy is the envelope of the lines that are parallel to the axes of a plane curve's osculating parabolas and pass through their point of contact with the plane curve.

The curve of aberrancy is the locus of the centers of aberrancy of a plane curve.

Examples

Basic Examples (2)

Define the parametric equations for an astroid:

In[1]:=

$astroid[a_, t_] := {a Cos[t]^3, a Sin[t]^3}$

Compute its curve of aberrancy:

In[2]:=

Out[2]=

Plot the astroid and its curve of aberrancy:

In[3]:=

$\[Alpha] = astroid[1, t]; \[Delta] = Simplify[ResourceFunction["AberrancyCurve"][astroid[1, t], t]]; ParametricPlot[Evaluate[{\[Alpha], \[Delta]}], {t, -3, 3}]$

Out[3]=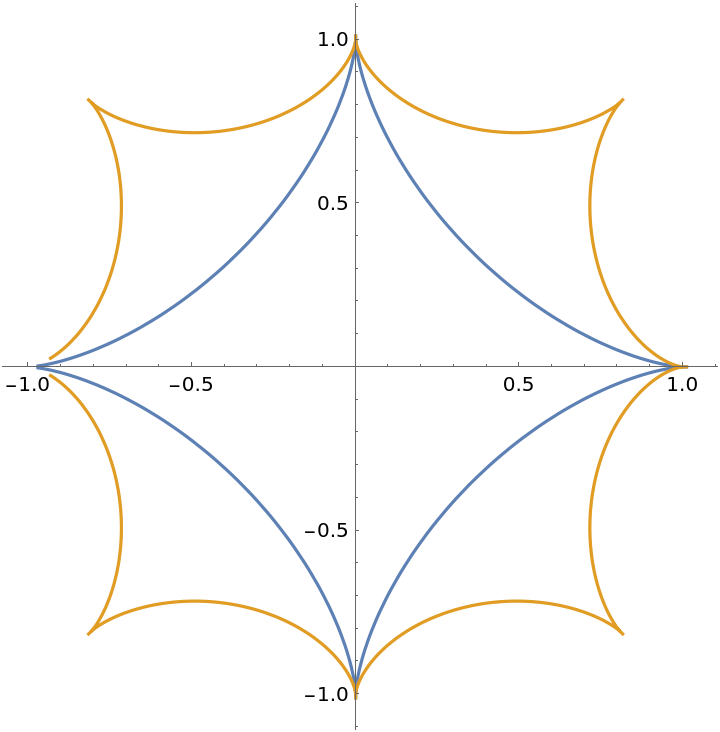

Compute the implicit equation for the curve of aberrancy of a quartic:

In[4]:=

$Eliminate[{x, y} == ResourceFunction["AberrancyCurve"][{t, t^4}, t], t]$

Out[4]=

Properties and Relations (1)

The curve of aberrancy of a plane curve involves third and fourth derivatives:

In[5]:=

Out[5]=

Version History

1.0.0 – 04 March 2021

Source Metadata

Citation:
- Gordon R.A., "The Aberrancy of Plane Curves." The Mathematical Gazette, vol. 89, no. 516, 424-436, 2005. DOI: 10.1017/S0025557200178271
- Schot S.H., "Aberrancy: Geometry of the Third Derivative." Mathematics Magazine, vol. 51, no. 5, 259-275, 1978. DOI: 10.1080/0025570X.1978.11976728
- Walker, A., "The differential equation of a conic and its relation to aberrancy." American Mathematical Monthly, vol. 59, 531–539, 1952. DOI: 10.1080/00029890.1952.11988184

Related Resources

License Information

This work is licensed under a Creative Commons Attribution 4.0 International License