Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 DihedralCanonicalization

Source Notebook

Return a canonical rotation/reflection for a point set

Contributed by: Ed Pegg Jr

ResourceFunction["DihedralCanonicalization"][points]

find a canonical rotation, reflection and ordering for 2D pointset points.

Details

This function is intended for usage in symmetry breaking. When a function on a set of points has a costly run time, symmetry breaking with ResourceFunction["DihedralCanonicalization"] can eliminate equivalent inputs.
Points with low norm and off lines of symmetry (x≠y≠0) will be sorted earlier.

Examples

Basic Examples (3) 

Canonicalize a set of points:

In[1]:=
pts = Reverse /@ {{-1, 4}, {2, -4}, {-3, 3}, {-4, -2}, {4, 2}, {3, -1}, {-2, -3}, {1, 1}}; canon = ResourceFunction["DihedralCanonicalization"][pts]
Out[1]=

Verify that applying the function to a canonicalized set returns the same set:

In[2]:=
ResourceFunction["DihedralCanonicalization"][canon]
Out[2]=

Show before/after to reveal the pattern has rotated counterclockwise:

In[3]:=
{Framed[Graphics[{Rectangle /@ pts}]], Framed[Graphics[{Rectangle /@ canon}]]}
Out[3]=

Scope (3) 

Find invariant pairs of points:

In[4]:=
pairs1 = Subsets[Tuples[Range[-1, 1], {2}], {2}]; invariants1 = Union[ResourceFunction["DihedralCanonicalization"] /@ pairs1]
Out[5]=

Find invariant pairs of points with maximal absolute value 2:

In[6]:=
pairs2 = Subsets[Tuples[Range[-2, 2], {2}], {2}]; invariants2 = Complement[ Union[ResourceFunction["DihedralCanonicalization"] /@ pairs2], invariants1]
Out[7]=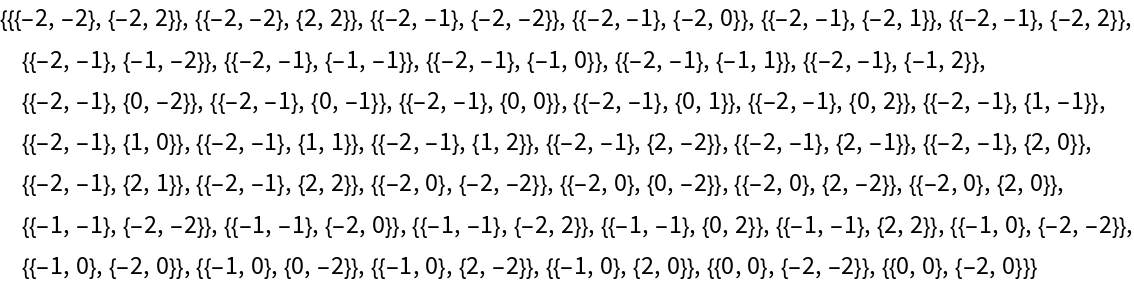

There are a few hundred of pairs2:

In[8]:=
Length[pairs2]
Out[8]=

The canonical invariants are a much smaller set:

In[9]:=
Length[invariants2]
Out[9]=

Count the number of invariants with maximal absolute value n:

In[10]:=
pairs7 = Subsets[Tuples[Range[-7, 7], {2}], {2}]; invariants7 = Union[ResourceFunction["DihedralCanonicalization"] /@ pairs7]; Length /@ GatherBy[SortBy[invariants7, Max[Abs[Flatten[#]]] &], Max[Abs[Flatten[#]]] &]
Out[11]=

Obtain values for a related cubic:

In[12]:=
Table[-1 + 5 n + 4 n^3, {n, 1, 10}]
Out[12]=

Find invariant triples:

In[13]:=
trip1 = Subsets[Tuples[Range[-1, 1], {2}], {3}]; invariants1 = Union[ResourceFunction["DihedralCanonicalization"] /@ trip1]
Out[14]=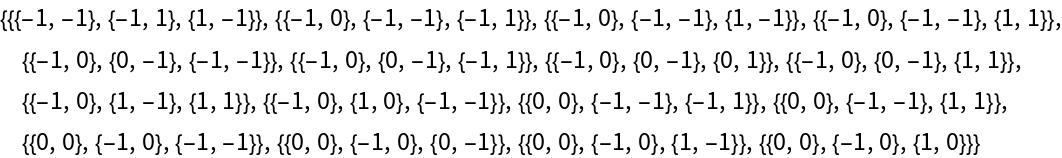

Show the 16 invariant triples:

In[15]:=
Grid[Partition[ Graphics[{EdgeForm[Black], {White, Rectangle[{-1.1, -1.1}, {1.1, 1.1}]}, Point[#], Circle[{0, 0}, .1]}, ImageSize -> 80] & /@ invariants1, 4]]
Out[15]=

Curiously, the number of invariant triples grows as follows:

In[16]:=
Table[(3 - 11 n + 24 n^2 + 8 n^3 + 24 n^5)/3, {n, 1, 10}]
Out[16]=

Possible Issues (1) 

Repeated points will be tossed out:

In[17]:=
points = RandomChoice[Tuples[Range[-1, 1], {2}], 10]
Out[17]=
In[18]:=
ResourceFunction["DihedralCanonicalization"][points]
Out[18]=

Requirements

Wolfram Language 14.0 (January 2024) or above

Version History

  • 1.0.0 – 12 May 2025

Related Resources

License Information