Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 UnitNormal

Source Notebook

Compute the unit normal of a surface

Contributed by: Alfred Gray

ResourceFunction["UnitNormal"][s,{u,v}]

gives the unit normal vector field to the surface s parametrized by variables u,v.

Details and Options

ResourceFunction["UnitNormal"] effectively computes the Gauss map of s that maps every point on a surface to a corresponding point on the unit sphere.

Examples

Basic Examples (3) 

Define a torus surface:

In[1]:=
torus = Entity["Surface", "Torus"]["ParametricEquations"][2, 3][u, v]
Out[1]=

Get the unit normals of the surface:

In[2]:=
normals = ResourceFunction["UnitNormal"][torus, {u, v}] // FullSimplify
Out[2]=

Plot the vector field:

In[3]:=
Show[ParametricPlot3D[torus, {u, 0, \[Pi]}, {v, -\[Pi], \[Pi]}, PlotStyle -> Opacity[.5]], Graphics3D[{Arrowheads[0.02], Arrow /@ Table[{torus, torus + normals}, {u, 0, \[Pi], 2 \[Pi]/20}, {v, -\[Pi], \[Pi], 2 \[Pi]/20}]}]]
Out[3]=

Scope (2) 

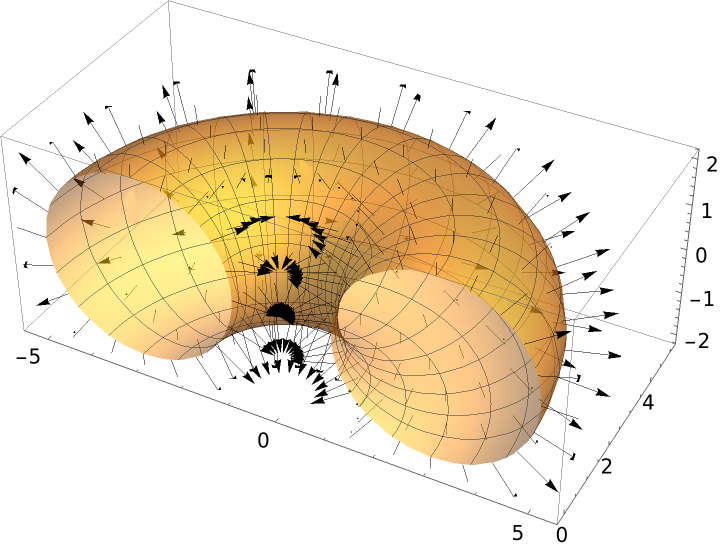Define a Möbius strip:

In[4]:=
mobius = Entity["Surface", "MoebiusStrip"]["ParametricEquations"][2, 3][u, v]
Out[4]=

Get the unit normals of the surface:

In[5]:=
normals = ResourceFunction["UnitNormal"][mobius, {u, v}] // FullSimplify
Out[5]=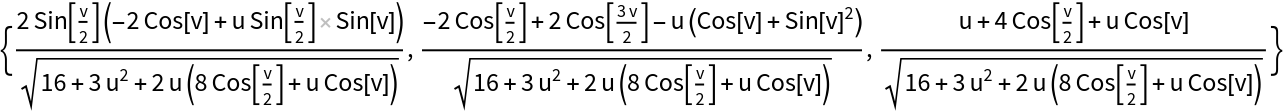

A Gauss map is not well defined on the whole surface, as unit normal vectors are only defined up to sign and there is no way to consistently decide the direction of the normal vector:

In[6]:=
Show[ParametricPlot3D[mobius, {u, 0, 2}, {v, 0, 4 \[Pi]}, PlotPoints -> 40], Graphics3D[{Arrowheads[0.02], Arrow /@ Table[{mobius, mobius + normals}, {u, 0, 2, .5}, {v, -2 \[Pi], 2 \[Pi], 2 \[Pi]/20}]}]]
Out[6]=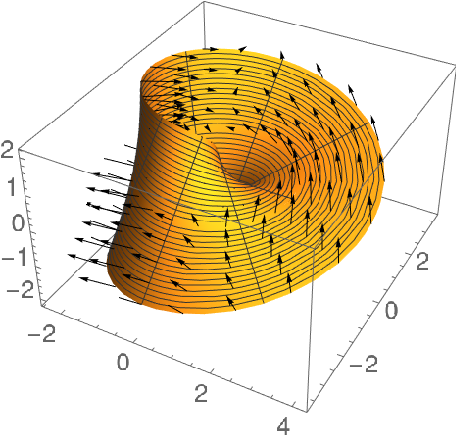

Define a sine surface:

In[7]:=
sine = Entity["Surface", "SineSurface"]["ParametricEquations"][1][u, v]
Out[7]=

Plot the sine surface:

In[8]:=
ParametricPlot3D[sine, {u, 0, 2 \[Pi]}, {v, 0, 2 \[Pi]}, PlotStyle -> Opacity[.5], Mesh -> None, PlotPoints -> 40]
Out[8]=

The parametrization of the unit normals of the sine surface:

In[9]:=
normals = ResourceFunction["UnitNormal"][sine, {u, v}] // FullSimplify
Out[9]=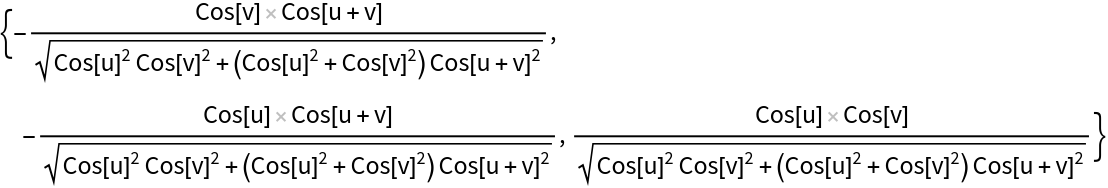

A Gauss map shows where the normals "live" inside the unit sphere:

In[10]:=
Show[Graphics3D[{Arrowheads[0.02], Arrow /@ Table[{{0, 0, 0}, normals /. u -> 1}, {v, 0.01, 2 \[Pi], 2 \[Pi]/40}], Opacity[.5], Sphere[]}], ParametricPlot3D[normals, {u, .8, 1.2}, {v, 0, 2 \[Pi]}, PlotStyle -> Opacity[.5], PlotPoints -> 40]]
Out[10]=

Publisher

Enrique Zeleny

Version History

  • 1.0.0 – 30 March 2020

Source Metadata

  • Citation:
    • Gray, A., Modern Differential Geometry of Curves and Surfaces with Mathematica, 2nd ed. Boca Raton, FL: CRC Press, 1997.

License Information