Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Generate an orthonormal basis from a given 3D vector
ResourceFunction["BasisFromVector"][v] generates an orthonormal basis from the numerical three-dimensional vector v. |
Generate an orthonormal basis from a real vector:
| In[1]:= |
|
| Out[1]= |
|
Verify orthonormality:
| In[2]:= |
|
| Out[2]= |
|
Generate an orthonormal basis from a complex vector:
| In[3]:= |
|
| Out[3]= |
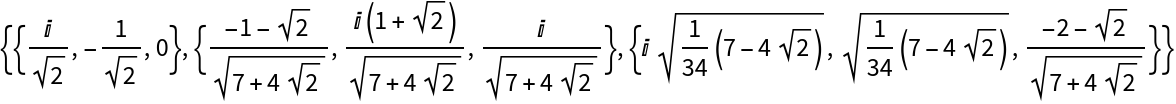
|
Verify orthonormality:
| In[4]:= |
|
| Out[4]= |
|
A rational-valued vector:
| In[5]:= |
|
| Out[5]= |
|
An exact complex vector:
| In[6]:= |
|
| Out[6]= |

|
An approximate MachinePrecision real vector:
| In[7]:= |
|
| Out[7]= |
|
An approximate MachinePrecision complex vector:
| In[8]:= |
|
| Out[8]= |
|
An approximate arbitrary-precision real vector:
| In[9]:= |
|
| Out[9]= |

|
An approximate arbitrary-precision complex vector:
| In[10]:= |
|
| Out[10]= |

|
Generate a random point on the sphere:
| In[11]:= |
|
| Out[11]= |
|
Construct the orthonormal basis:
| In[12]:= |
|
| Out[12]= |
|
Visualize the basis vectors:
| In[13]:= |
|
| Out[13]= |

|
BasisFromVector only generates one out of many possible orthonormal bases:
| In[14]:= |
|
| Out[14]= |
|
BasisFromVector always generates a right-handed basis:
| In[15]:= |
|
| Out[15]= |
|
| In[16]:= |
|
| Out[16]= |
|
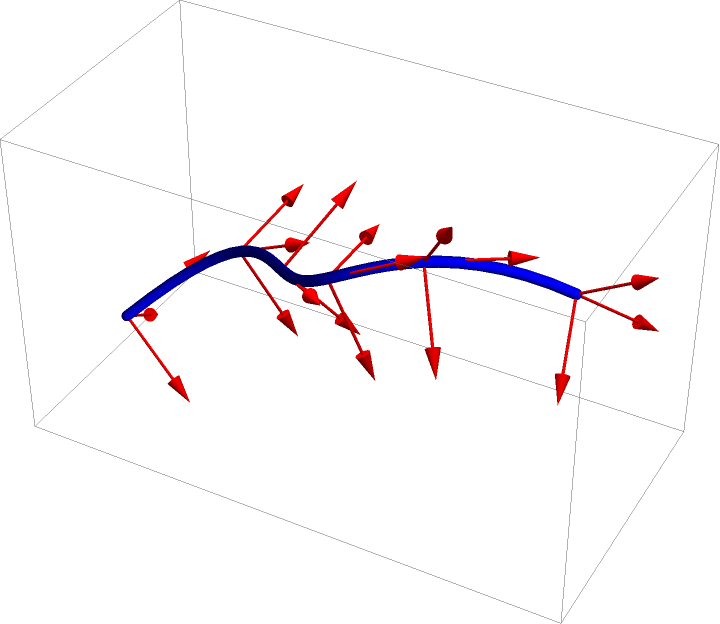
Generate a set of orthonormal frames along a curve:
| In[17]:= |
![cpts = {{0, 0, 0}, {1, 1, 1}, {2, -1, 1}, {3, 0, 2}, {4, 1, 1}};
bf = BSplineFunction[cpts];
pts = Table[bf[t], {t, 0, 1, 1/5}];
bList = Table[
TranslationTransform[bf[t]][
ResourceFunction["BasisFromVector"][bf'[t]]], {t, 0, 1, 1/5}];
Graphics3D[{{Blue, Tube[BSplineCurve[cpts], 1/20]}, {Red, MapThread[
Map[Function[v, Arrow[Tube[{#1, v}]]], #2] &, {pts, bList}]}}]](https://www.wolframcloud.com/obj/resourcesystem/images/9e9/9e957eb0-e391-43b8-a5ee-81a2e7aeb96c/5d511d4065c014ad.png)
|
| Out[17]= |
|
This work is licensed under a Creative Commons Attribution 4.0 International License