Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 EisensteinIntegers

Source Notebook

Support arithmetic operations for pairs of Eisenstein integers

Contributed by: Daniel Lichtblau

ResourceFunction["EisensteinIntegers"][n,"operator"]

returns the result of applying unary operation "operator" to the Eisenstein integer n.

ResourceFunction["EisensteinIntegers"][n1,n2,"operator"]

returns the result of applying binary operation "operator" to n1 and n2.

ResourceFunction["EisensteinIntegers"][n1,…,ω,"operator"]

uses ω to represent the Eisenstein ring extension element .

Details

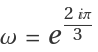
The ring of Eisenstein integers is ℤ[ω], where is a primitive third root of unity.
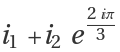
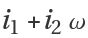
ResourceFunction["EisensteinIntegers"] supports two representations: an Eisenstein integer can be given either as a pair {i1,i2}, which denotes , or as . In the latter case, the symbol used to denote the extension element, ω, must be given explicitly in all operations.
The norm of an Eisenstein integer is defined as the product of the integer with its complex conjugate. The conjugate of ω is .
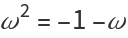
There are six units in the ring of Eisenstein integers: {±1,±ω,±ω2=∓(1+ω)}. An Eisenstein integer is a unit if and only if its norm is 1.
Supported unary operations are "Re", "Im", "ReIm", "Conjugate", "Norm", "Abs", "Reciprocal", "UnitQ", "PrimeQ" and "FactorInteger".
The conjugate of ω is ω2. This is equal to -1-ω due to the fundamental identity ω2+ω+1=0. ResourceFunction["EisensteinIntegers"] always reduces by this identity, so ω2 is never used in a result (and is not supported in input).
Supported binary operations are "Plus", "Times", "Power", "Dot", "Quotient", "Remainder", "QuotientRemainder", "AssociatesQ", "DividesQ","IntegerExponent", "GCD" and "ExtendedGCD".
Except where specified otherwise, all supported operations in effect do what the corresponding functions do with ordinary or Gaussian integers.
ResourceFunction["EisensteinIntegers"] supports "Power" when the second argument is an explicit nonnegative integer.
Ordinary multiplication is used in "Dot", that is, no conjugation takes place.
ResourceFunction["EisensteinIntegers"] also supports "ListPlus" and "ListTimes" so one can give a list of arguments for adding or multiplying.
ResourceFunction["EisensteinIntegers"] also supports "PowerMod". The power must be a nonnegative integer. The modulus must be an Eisenstein integer.
ResourceFunction["EisensteinIntegers"] regards the multiplier of the extension element as the "imaginary" part, even though it has both a real and an imaginary component in the complex plane.
The Eisenstein integer a+b ω has norm a2+b2-ab. The absolute value is the square root of the norm.
Unary operations and binary operations that do not use division allow symbolic input—that is, Eisenstein numbers that are not expressed using explicit integers.
The reciprocal operation will in general return an Eisenstein rational rather than an integer. All other operations return integers when given explicit Eisenstein integer inputs.

Examples

Basic Examples (6) 

Find the norm of an Eisenstein integer:

In[1]:=
e = 3 + 7 w; ResourceFunction["EisensteinIntegers"][e, w, "Norm"]
Out[1]=

Find its conjugate:

In[2]:=
ce = ResourceFunction["EisensteinIntegers"][e, w, "Conjugate"]
Out[2]=

Verify that the norm is the product of the number and its conjugate:

In[3]:=
ResourceFunction["EisensteinIntegers"][e, ce, w, "Times"]
Out[3]=

The absolute value of an Eisenstein number is the same as that of the complex number equivalent:

In[4]:=
{ResourceFunction["EisensteinIntegers"][{3, 7}, "Abs"], Abs[3 + 7 Exp[2*I*Pi/3]]}
Out[4]=

Find the reciprocal of an Eisenstein integer:

In[5]:=
r = ResourceFunction["EisensteinIntegers"][9 - 11 w, w, "Reciprocal"]
Out[5]=

Verify that it is the reciprocal:

In[6]:=
ResourceFunction["EisensteinIntegers"][9 - 11 w, r, w, "Times"]
Out[6]=

Multiply a pair of Eisenstein integers:

In[7]:=
e0 = 3 + 7 w; e1 = 2 - 7 w; eprod = ResourceFunction["EisensteinIntegers"][e0, e1, w, "Times"]
Out[7]=

The product cannot be a prime:

In[8]:=
ResourceFunction["EisensteinIntegers"][eprod, w, "PrimeQ"]
Out[8]=

Show that both factors are prime:

In[9]:=
Map[ResourceFunction["EisensteinIntegers"][#, w, "PrimeQ"] &, {e0, e1}]
Out[9]=

Divide a pair of Eisenstein integers:

In[10]:=
ResourceFunction["EisensteinIntegers"][9 - 11 w, 3 + 7 w, w, "Quotient"]
Out[10]=

Find the quotient and remainder of a pair of Eisenstein integers:

In[11]:=
{quo, rem} = ResourceFunction["EisensteinIntegers"][9 - 11 w, 3 + 7 w, w, "QuotientRemainder"]
Out[11]=

Recover the dividend from divisor, quotient and remainder:

In[12]:=
ResourceFunction["EisensteinIntegers"][ ResourceFunction["EisensteinIntegers"][3 + 7 w, quo, w, "Times"], rem, w, "Plus"]
Out[12]=

Scope (6) 

Use the ordered pair representation:

In[13]:=
ResourceFunction[ "EisensteinIntegers"][{9, -11}, {3, 7}, "QuotientRemainder"]
Out[13]=

Multiply a pair of Eisenstein numbers with symbolic values for real and imaginary parts:

In[14]:=
ResourceFunction[ "EisensteinIntegers"][(a + w b), (c + w d), w, "Times"]
Out[14]=

Form the dot product of two vectors of Eisenstein integers:

In[15]:=
ResourceFunction[ "EisensteinIntegers"][{3 + w, 2 + 3 w, 4 + 7 w}, {-2 - w, w, 3 + 5 w}, w, "Dot"]
Out[15]=

Repeat, using the list representation for the Eisenstein integers:

In[16]:=
ResourceFunction[ "EisensteinIntegers"][{{3, 1}, {2, 3}, {4, 7}}, {{-2, -1}, {0, 1}, {3, 5}}, "Dot"]
Out[16]=

Compute the GCD of a pair of Eisenstein integers:

In[17]:=
e0 = 3 + 7 w; e1 = ResourceFunction["EisensteinIntegers"][e0, 4 + 5 w, w, "Times"]; e2 = ResourceFunction["EisensteinIntegers"][e0, 6 - 7 w, w, "Times"]; g = ResourceFunction["EisensteinIntegers"][e1, e2, w, "GCD"]
Out[17]=

Check that it divides both inputs:

In[18]:=
Map[ResourceFunction["EisensteinIntegers"][g, #, w, "DividesQ"] &, {e1, e2}]
Out[18]=

Compute the extended GCD of this pair:

In[19]:=
eg = ResourceFunction["EisensteinIntegers"][e1, e2, w, "ExtendedGCD"]
Out[19]=

Show that we recover the GCD from the Bezout relation:

In[20]:=
ResourceFunction["EisensteinIntegers"][{e1, e2}, eg[[2]], w, "Dot"]
Out[20]=

Check that the GCD is an associate of the common factor used to form the inputs:

In[21]:=
ResourceFunction["EisensteinIntegers"][g, e0, w, "AssociatesQ"]
Out[21]=

Raise 11-7w to power 20 modulo 14+9w:

In[22]:=
ResourceFunction["EisensteinIntegers"][11 - 7*w, 20, 14 + 9 w, w, "PowerMod"]
Out[22]=

Create some Eisenstein primes:

In[23]:=
SeedRandom[1234]; enums = RandomInteger[{-5, 5}, {16, 2}]; eprims = Select[enums, ResourceFunction["EisensteinIntegers"][#, "PrimeQ"] &]
Out[23]=

No pair are associates:

In[24]:=
Table[ResourceFunction["EisensteinIntegers"][eprims[[i]], eprims[[j]], "AssociatesQ"], {i, Length[eprims] - 1}, {j, i + 1, Length[eprims]}] // Flatten
Out[24]=

Raise these primes to successive powers:

In[25]:=
primepowers = MapIndexed[ ResourceFunction["EisensteinIntegers"][#1, #2[[1]], "Power"] &, eprims]
Out[25]=

Take the product of these powers:

In[26]:=
powerprod = ResourceFunction["EisensteinIntegers"][primepowers, "ListTimes"]
Out[26]=

Now factor it:

In[27]:=
pfacs = ResourceFunction["EisensteinIntegers"][powerprod, "FactorInteger"]
Out[27]=

Check that each factor after the initial unit is an Eisenstein prime:

In[28]:=
Map[ResourceFunction["EisensteinIntegers"][#, "PrimeQ"] &, pfacs[[2 ;;, 1]]]
Out[28]=

Expand the factors to their specified powers:

In[29]:=
pows = Map[ ResourceFunction["EisensteinIntegers"][#[[1]], #[[2]], "Power"] &, pfacs]
Out[29]=

Check that expanding the factorization recovers the product:

In[30]:=
ResourceFunction["EisensteinIntegers"][pows, "ListTimes"] == powerprod
Out[30]=

Neat Examples (2) 

The GCD implementation for EisensteinIntegers uses an asymptotically fast method that performs better than the standard Euclidean sequence method:

In[31]:=
(* Evaluate this cell to get the example input *) CloudGet["https://www.wolframcloud.com/obj/9cdc71b5-7ff3-427e-bcab-ffb73207ea80"]
Out[31]=

Here is a version of the Euclidean sequence method:

In[32]:=
(* Evaluate this cell to get the example input *) CloudGet["https://www.wolframcloud.com/obj/e2593eb2-8fa1-4441-90d8-dad97f8e723a"]

Time it on the same example:

In[33]:=
Timing[gcd2 = EisensteinEuclideanGCD[e1, e2];]
Out[33]=

Check that the results are equivalent:

In[34]:=
ResourceFunction["EisensteinIntegers"][gcd, gcd2, "AssociatesQ"]
Out[34]=

Double the size and repeat the timing:

In[35]:=
(* Evaluate this cell to get the example input *) CloudGet["https://www.wolframcloud.com/obj/284cccfd-853a-411b-83f1-c7f538dfc27c"]
Out[35]=

Now repeat the Euclidean sequence computation:

In[36]:=
Timing[gcd2 = EisensteinEuclideanGCD[e1, e2];]
Out[36]=

Do this again:

In[37]:=
(* Evaluate this cell to get the example input *) CloudGet["https://www.wolframcloud.com/obj/bea72e8a-276f-44cb-9277-aecc98f4175f"]
Out[37]=

Again repeat the Euclidean sequence computation:

In[38]:=
Timing[gcd2 = EisensteinEuclideanGCD[e1, e2];]
Out[38]=

Check that the known factor e0 is a divisor of the GCD:

In[39]:=
ResourceFunction["EisensteinIntegers"][e0, gcd, "DividesQ"]
Out[39]=

Show the first 18 powers of 7/6+ω:

In[40]:=
Graphics[RegularPolygon[ReIm[#], {1/2, \[Pi]/2}, 6] & /@ Table[ResourceFunction["EisensteinIntegers"][7/6 + \[Omega], n, \[Omega], "Power"], {n, 18}] /. \[Omega] -> Exp[2 Pi I/3]]
Out[40]=

Version History

  • 1.1.1 – 02 June 2021

Source Metadata

  • Citation:
    • Agarwal, S., Frandsen, G.S., "A new GCD Algorithm for Quadratic Number Rings with Unique Factorization." In: Correa, J.R., Hevia, A., Kiwi, M. (eds), LATIN 2006: Theoretical Informatics: 7th Latin American Symposium, Valdivia, Chile, March 20-24, 2006. Proceedings. Lecture Notes in Computer Science 3887, 30-42. Berlin, Heidelberg: Springer-Verlag, 2006. https://link.springer.com/chapter/10.1007/11682462_8

Related Resources

Author Notes

The method for computing GCDs of Eisenstein integers has complexity of . This is the soft-oh notation that indicates presence of logarithmic factors, which in this case would be log2n log log n.
The half-GCD style method has similar complexity when implemented with an optimal lattice reduction method, albeit with a heftier multiplicative constant in the . The method used in the actual GCD code is substantially similar to the one described in "A new GCD Algorithm for Quadratic Number Rings with Unique Factorization" by Saurabh Agarwal and Gudmund Skovbjerg Frandsen. That method is difficult to adapt for extended GCDs because the size of the Bezout multipliers is not well controlled. So a half-GCD approach is taken, using a reasonably fast lattice reduction. It is considerably faster than a Euclidean remainder sequence.

License Information