Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Approximate the surface area of a molecule
ResourceFunction["MoleculeBuriedResiduesIndex"][mol] approximates the internal interface surface area of mol in relative terms. |
Compute the internal surface area of a water molecule:
| In[1]:= |
| Out[1]= |
Approximate the internal surface area of two different molecules to compare them:
| In[2]:= | ![molecule1 = Molecule[Entity["Chemical", "Caffeine"]];
molecule2 = Molecule[Entity["Chemical", "Water"]];](https://www.wolframcloud.com/obj/resourcesystem/images/9d8/9d81ee34-2f6c-42c5-95e1-e005f3649658/6f1b1aa9015ea04e.png) |
| In[3]:= |
| Out[3]= |
| In[4]:= |
| Out[4]= |
The more complex molecule has greater internal surface area, as expected. See the molecules to understand why caffeine has more internal area than water:
| In[5]:= |
| Out[5]= | 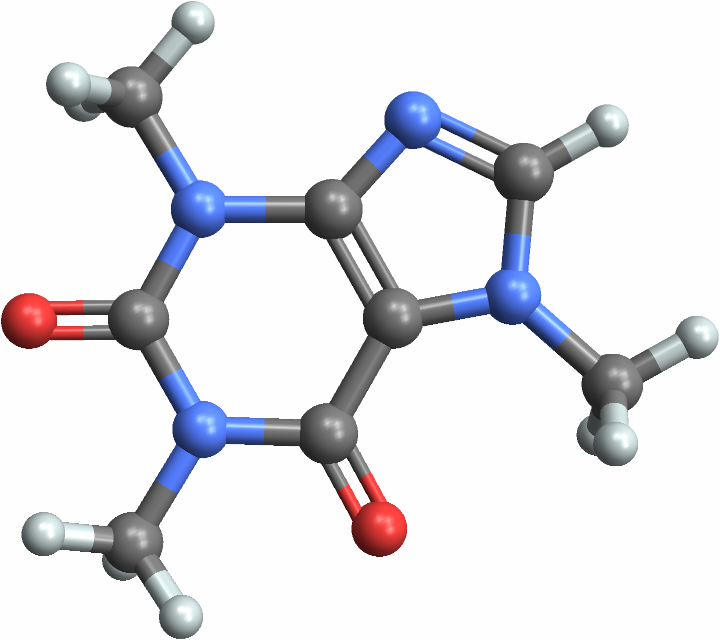 |
| In[6]:= |
| Out[6]= | 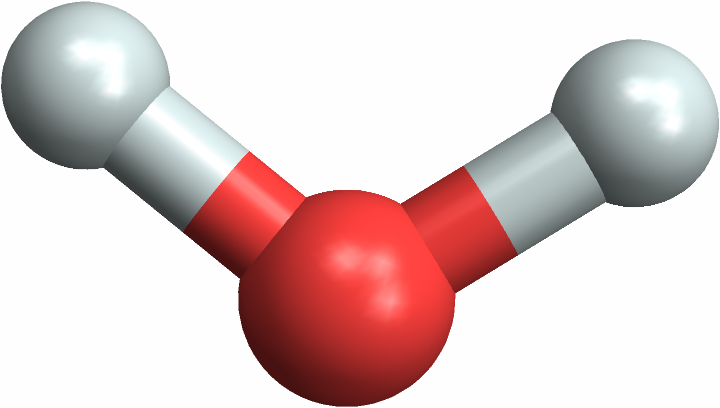 |
Increasing the density (of the distribution of test points in the molecule) will increase accuracy, but also increase time cost:
| In[7]:= |
| Out[7]= |
| In[8]:= | ![AbsoluteTiming /@ {ResourceFunction["MoleculeBuriedResiduesIndex"][
testingMolecule, Density -> 2],
ResourceFunction["MoleculeBuriedResiduesIndex"][testingMolecule, Density -> 8]}](https://www.wolframcloud.com/obj/resourcesystem/images/9d8/9d81ee34-2f6c-42c5-95e1-e005f3649658/42094f807d16c4d1.png) |
| Out[8]= |
Wolfram Language 13.0 (December 2021) or above
This work is licensed under a Creative Commons Attribution 4.0 International License