Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 RowSpaceBasis

Source Notebook

Return a basis for the subspace spanned by the rows of the matrix

Contributed by: Dennis M Schneider

ResourceFunction["RowSpaceBasis"][mat]

returns the reduced-echelon basis of the row space of mat.

Details and Options

The vectors returned by ResourceFunction["RowSpaceBasis"] are the nonzero rows in the reduced echelon form of the matrix. In general, these vectors will be different from the rows of the matrix, but they will span the same subspace as the rows of the matrix.
To find a basis for the row space comprised of rows of the original matrix, use the fact that the row space of a matrix is equal to the column space of the transpose of the matrix. Since ColumnSpaceBasis[Transpose[mat]] returns a subset of the original columns of Transpose[mat] that span the column space, these basis vectors will span the rowspace of mat.

Examples

Basic Examples (2) 

Compute the row space basis of an input matrix:

In[1]:=
ResourceFunction[ "RowSpaceBasis"][{{1, 3, -2, 1}, {2, 6, -2, 8}, {-1, -3, 8, 17}}]
Out[1]=

Check that the reduced echelon forms have the same nonzero vectors:

In[2]:=
RowReduce[{{1, 3, -2, 1}, {2, 6, -2, 8}, {-1, -3, 8, 17}}]
Out[2]=
In[3]:=
RowReduce[{{1, 3, 0, 7}, {0, 0, 1, 3}}]
Out[3]=

Basic Scope (3) 

Define a matrix with complex entries:

In[4]:=
(mat = {{2, 1, 1 - I, 1 + I, 1 + I, 2 + 2 I}, {I, -I, 2 + 2 I, 1 + 2 I, 1 + I, 2 - I}, {-I, 1, -1 + I, -I, -1 + I, 2 - I}, {13 + 5 I, -1 + 6 I, 14 - 18 I, 5 - 3 I, 5 + I, -15 + 9 I}}) // MatrixForm
Out[4]=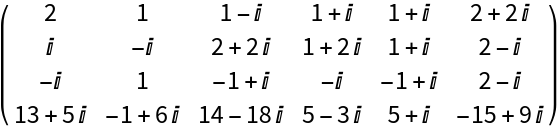

Find the row space basis of it:

In[5]:=
ResourceFunction["RowSpaceBasis"][mat]
Out[5]=

Check the result:

In[6]:=
RowReduce[mat]
Out[6]=
In[7]:=
RowReduce[ResourceFunction["RowSpaceBasis"][mat]]
Out[7]=

Publisher

Dennis M Schneider

Version History

  • 1.0.0 – 08 August 2019

Related Resources

License Information