Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Evaluate the Clausen function
ResourceFunction["ClausenCl"][n,z] gives the Clausen function Cln(z). |
Evaluate numerically:
| In[1]:= |
| Out[1]= |
Plot the first few Clausen functions:
| In[2]:= |
| Out[2]= | 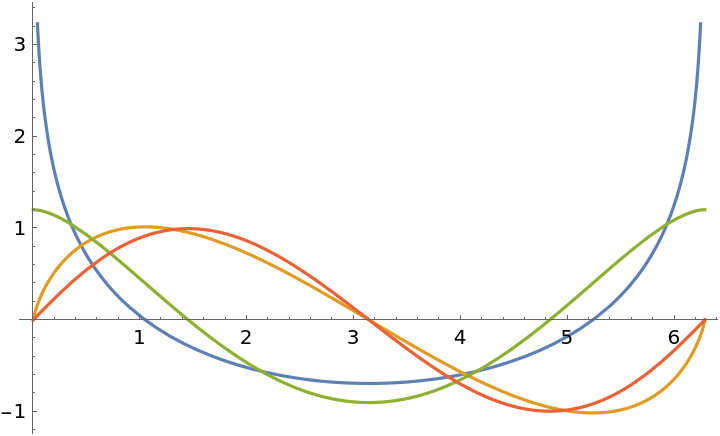 |
Evaluate for complex arguments and parameters:
| In[3]:= |
| Out[3]= |
Evaluate to high precision:
| In[4]:= |
| Out[4]= |
The precision of the output tracks the precision of the input:
| In[5]:= |
| Out[5]= |
Simple exact values are generated automatically:
| In[6]:= |
| Out[6]= |
| In[7]:= |
| Out[7]= |
ClausenCl threads elementwise over lists:
| In[8]:= |
| Out[8]= |
Parity transformations and periodicity relations are automatically applied:
| In[9]:= |
| Out[9]= |
| In[10]:= |
| Out[10]= |
| In[11]:= |
| Out[11]= |
Plots of the Clausen function in the complex plane:
| In[12]:= |
| Out[12]= | 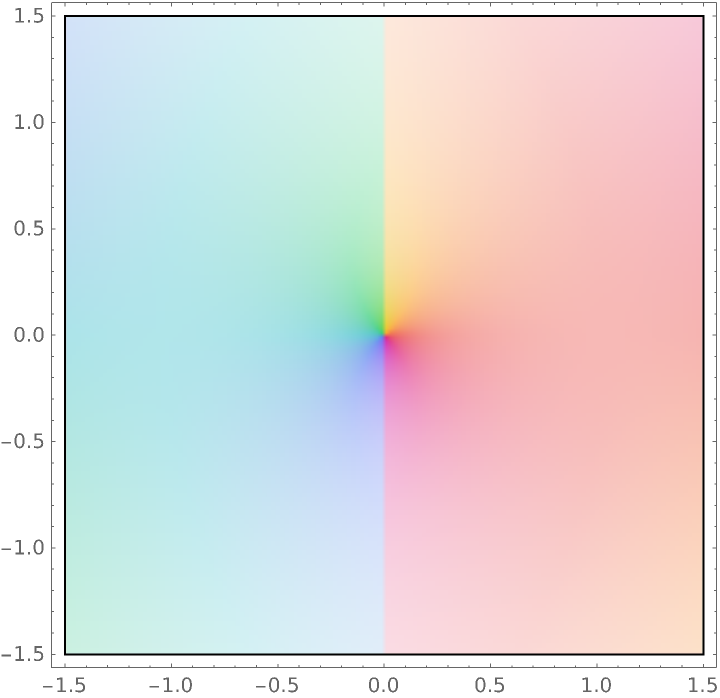 |
| In[13]:= | ![Plot3D[Im[ResourceFunction["ClausenCl"][1, x + I y]], {x, -1.5, 1.5}, {y, -1.7, 1.7}, ColorFunction -> "DarkRainbow", Mesh -> 20, MeshFunctions -> (#3 &), PlotPoints -> 30]](https://www.wolframcloud.com/obj/resourcesystem/images/9a0/9a0e9a32-1e72-49d7-a59d-d45d71b9c31d/32c8325f3f359f96.png) |
| Out[13]= | 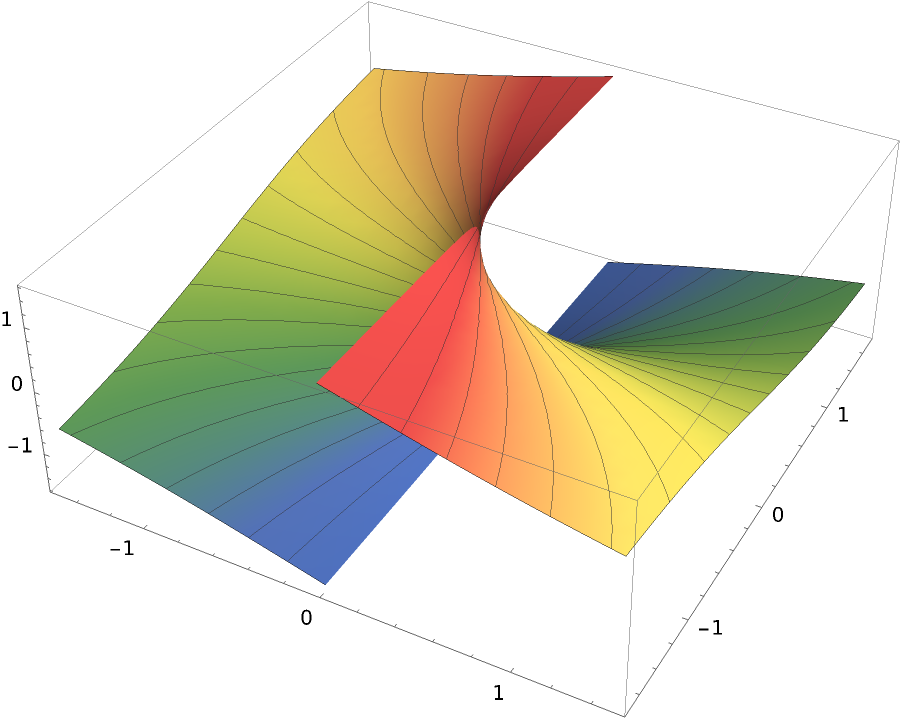 |
The Clausen function can be expressed in terms of PolyLog:
| In[14]:= | ![Table[ResourceFunction["ClausenCl"][n, z] == If[OddQ[n], (PolyLog[n, E^(I z)] + PolyLog[n, E^(-I z)])/2, (
PolyLog[n, E^(I z)] - PolyLog[n, E^(-I z)])/(2 I)] /. z -> RandomComplex[WorkingPrecision -> 20], {n, 1, 9}]](https://www.wolframcloud.com/obj/resourcesystem/images/9a0/9a0e9a32-1e72-49d7-a59d-d45d71b9c31d/588ebfd5d5537922.png) |
| Out[14]= |
The Clausen function appears in the reflection formula for BarnesG:
| In[15]:= | ![Log[BarnesG[1 + z]/BarnesG[1 - z]] == z Log[\[Pi] Csc[\[Pi] z]] - ResourceFunction["ClausenCl"][2, 2 \[Pi] z]/(2 \[Pi]) /. z -> RandomReal[WorkingPrecision -> 20]](https://www.wolframcloud.com/obj/resourcesystem/images/9a0/9a0e9a32-1e72-49d7-a59d-d45d71b9c31d/702ff8693a6f288d.png) |
| Out[15]= |
Verify a relationship between the Clausen function and the inverse tangent integral:
| In[16]:= | ![ResourceFunction["ArcTanIntegral"][2, Tan[u]] == u Log[Tan[u]] + (
ResourceFunction["ClausenCl"][2, 2 u] + ResourceFunction["ClausenCl"][2, \[Pi] - 2 u])/2 /. u -> RandomReal[WorkingPrecision -> 20]](https://www.wolframcloud.com/obj/resourcesystem/images/9a0/9a0e9a32-1e72-49d7-a59d-d45d71b9c31d/6b19ea805ccc5bdb.png) |
| Out[16]= |
Verify the duplication theorem:
| In[17]:= |
| Out[17]= |
Values of the Clausen function at rational multiples of π can be expressed in terms of PolyGamma:
| In[18]:= | ![With[{p = 3, q = 7}, Table[N[ResourceFunction["ClausenCl"][m, (\[Pi] p)/q] == (-1)^
Binomial[m + 1, 2]/((2 q)^m (m - 1)!) \!\(
\*UnderoverscriptBox[\(\[Sum]\), \(j = 1\), \(q\)]\(Sin[
\*FractionBox[\(\[Pi]\ p\), \(q\)] j +
\*FractionBox[\(m\ \[Pi]\), \(2\)]] \((PolyGamma[m - 1,
\*FractionBox[\(j\), \(2 q\)]] +
\*SuperscriptBox[\((\(-1\))\), \(p\)] PolyGamma[m - 1,
\*FractionBox[\(j + q\), \(2 q\)]])\)\)\), 20], {m, 10}]]](https://www.wolframcloud.com/obj/resourcesystem/images/9a0/9a0e9a32-1e72-49d7-a59d-d45d71b9c31d/46cf265c4d7f8198.png) |
| Out[18]= |
Wolfram Language 11.3 (March 2018) or above
This work is licensed under a Creative Commons Attribution 4.0 International License