Basic Examples (2)
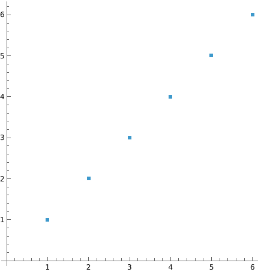
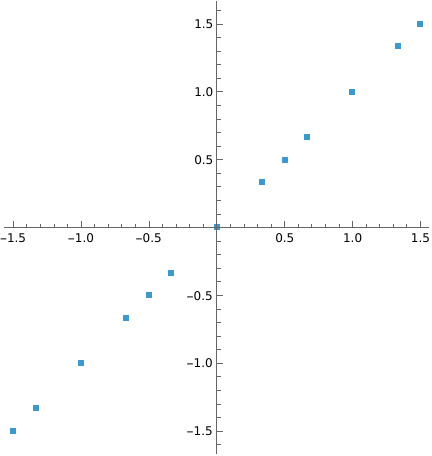
Create a linear range between two complex numbers:
Visualize it in the complex plane:
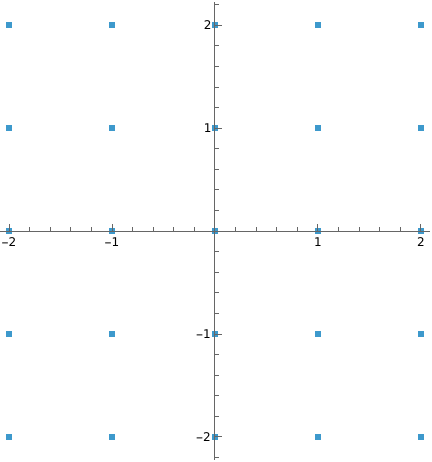
Create a rectangular range between two complex numbers:
Visualize it in the complex plane:
Scope (5)
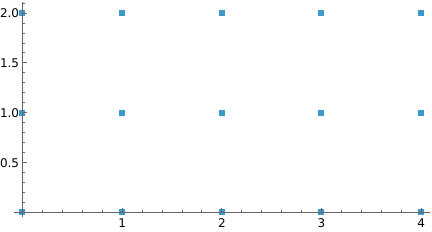
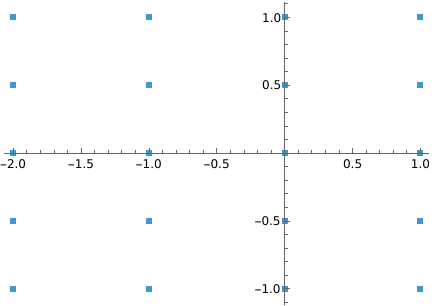
Create a rectangular range between 0 and a given complex number:
Visualize it in the complex plane:
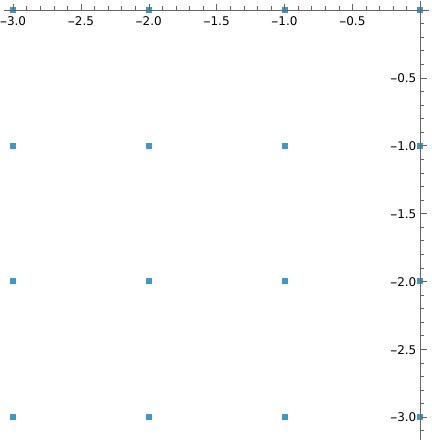
The range can be in any quadrant of the complex plane:
The step subdivisions can be specified as a complex number:
Alternatively, the third argument can be a list of the real and imaginary steps:
It is also possible to create a linear range, by wrapping the first two arguments in a list:
Options (6)
IncrementFirst (3)
By default, the imaginary part is incremented first:
To increment first the real part, use the option "IncrementFirst" → Re:
Of course, their Union is the same:
FareyRange (3)
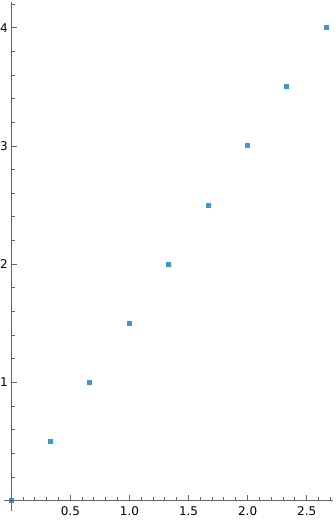
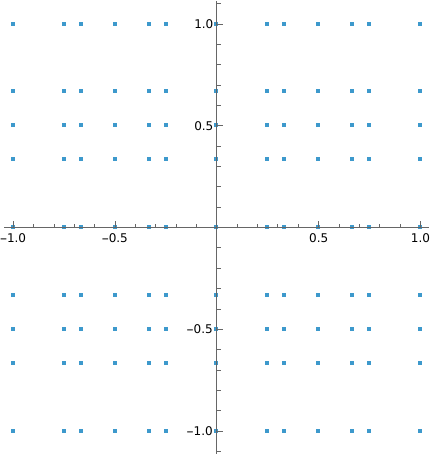
It is possible to specify a special range, namely the complex generalization of the resource function FareyRange:
The third argument is then the third argument of the resource function FareyRange, possibly different for the real and imaginary parts:
If the third argument is not a list of integers, a failure is returned:
Properties and Relations (3)
ComplexRange[z1,z2,z3] can be realized by combining Range and Outer. That is, ComplexRange[z1,z2,z3] is equivalent to Flatten@Outer[#1+ⅈ#2&,Range[Re[z1],Re[z2],Re[z3]],Range[Im[z1],Im[z2],Im[z3]]]:
ComplexRange[z1,z2,z3] can be also realized by combining Range and Tuples. That is, ComplexRange[z1,z2,z3] is equivalent to Plus@@@Tuples[{Range[Re[z1],Re[z2],Re[z3], ⅈRange[Im[z1],Im[z2],Im[z3]]}]:
ComplexRange[z1,z2,z3] can be also realized through CoordinateBoundsArray. That is, ComplexRange[z1,z2,z3] is equivalent to Plus@@@MapAt[# ⅈ&,Flatten[CoordinateBoundsArray[{{Re[z1],Re[z2]},{Im[z1],Im[z2]}},{Re[z3],Im[z3]}],1],{All,2}]:
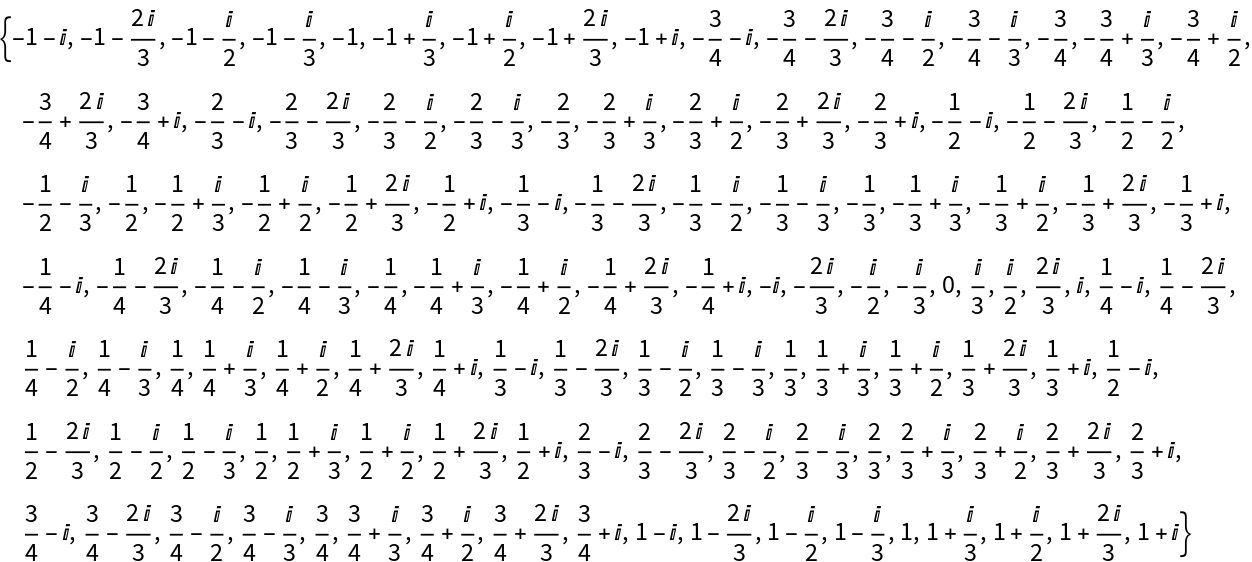
![ComplexListPlot[
{ResourceFunction["ComplexRange"][-3 - 3 I, 3 + 3 I, {3, 3}, "FareyRange" -> True],
ResourceFunction["ComplexRange"][-3 - 3 I, 3 + 3 I],
ResourceFunction["ComplexRange"][-5/2 - 5/2 I, 5/2 + 5/2 I],
ResourceFunction["ComplexRange"][-3 - 3 I, 3 + 3 I, {1/2, 1/2}]},
PlotMarkers ->
{{Automatic, Small}, {Automatic, Small}, {Automatic, Medium}, {Automatic, Tiny}},
Background -> Black, ImageSize -> Large]](https://www.wolframcloud.com/obj/resourcesystem/images/98b/98b27f81-d789-4689-a84d-9b8b61e06308/36a43f6568753d48.png)
