Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Perform multiple operations on an input in a neural net
ResourceFunction["NetParallelOperator"][{net1,net2,…}] represents a net with a single input and multiple outputs which correspond to applying the different networks to the input. | |
ResourceFunction["NetParallelOperator"][<|out1→ net1,out2→net2,…|>] specifies that the output of neti should be linked to output port outi. | |
ResourceFunction["NetParallelOperator"][spec, cat] uses a layer or net to combine the outputs into a single array again. | |
ResourceFunction["NetParallelOperator"][spec,Automatic] catenates the outputs sequentially using CatenateLayer[0]. |
Define a net that computes the Sin, Cos and Tan of an input:
| In[1]:= | ![net = ResourceFunction[
"NetParallelOperator"][{ElementwiseLayer[Sin], ElementwiseLayer[Cos], ElementwiseLayer[Tan] }]](https://www.wolframcloud.com/obj/resourcesystem/images/980/9808d3e0-eb5b-4acd-8981-74b86f648375/6aef9eb7288bbfb6.png) |
| Out[1]= | 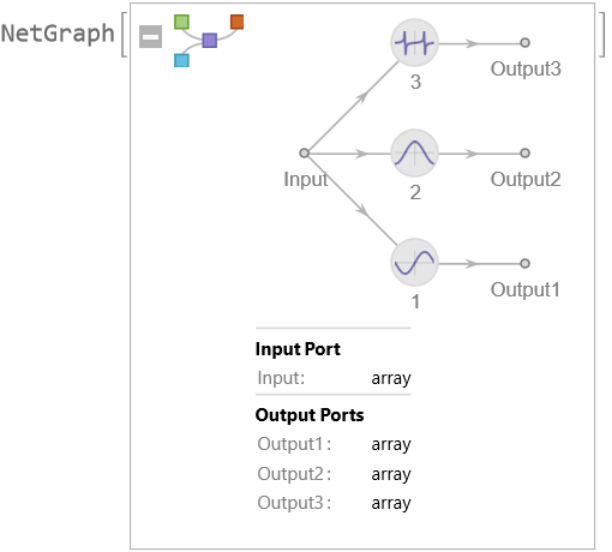 |
Apply it to one or more values:
| In[2]:= |
| Out[2]= |
| In[3]:= |
| Out[3]= |  |
Specify custom names for the output ports:
| In[4]:= | ![net = ResourceFunction[
"NetParallelOperator"][<|"sin" -> ElementwiseLayer[Sin], "cos" -> ElementwiseLayer[Cos], "tan" -> ElementwiseLayer[Tan]|>]](https://www.wolframcloud.com/obj/resourcesystem/images/980/9808d3e0-eb5b-4acd-8981-74b86f648375/46619da33542c046.png) |
| Out[4]= | 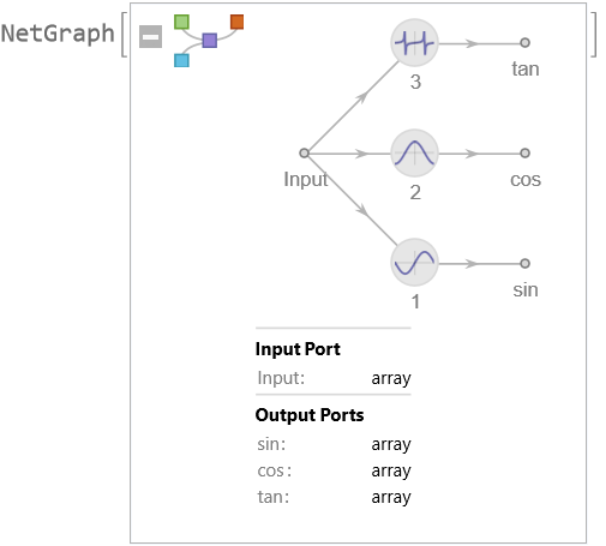 |
| In[5]:= |
| Out[5]= |
Convert the output to a single array again by joining the results:
| In[6]:= | ![net = ResourceFunction["NetParallelOperator"][
{ElementwiseLayer[Sin], ElementwiseLayer[Cos], ElementwiseLayer[Tan] },
Automatic
]](https://www.wolframcloud.com/obj/resourcesystem/images/980/9808d3e0-eb5b-4acd-8981-74b86f648375/526619e4feede365.png) |
| Out[6]= |
| In[7]:= |
| Out[7]= |
| In[8]:= |
| Out[8]= |
Use a different operation for combining the results into tuples:
| In[9]:= | ![net = ResourceFunction["NetParallelOperator"][
{ElementwiseLayer[Sin], ElementwiseLayer[Cos], ElementwiseLayer[Tan] },
NetChain[{CatenateLayer[0], TransposeLayer[]}]
]](https://www.wolframcloud.com/obj/resourcesystem/images/980/9808d3e0-eb5b-4acd-8981-74b86f648375/3cf328d1ebd89532.png) |
| Out[9]= |
| In[10]:= |
| Out[10]= |
Create a network that can find a matrix with specific row and column sums while keeping the size of the elements as small as possible. NetParallelOperatorcan be used to calculate the required sums:
| In[11]:= | ![net = ResourceFunction["NetParallelOperator"][
<|
"RowSums" -> AggregationLayer[Total, 2],
"ColumnSums" -> AggregationLayer[Total, 1],
"SumOfSquares" -> NetChain[{
ElementwiseLayer[0.01*#^2 &],(* Multiply this with a small scaling factor to make sure the row and column losses are treated with higher priority during training *)
AggregationLayer[Total, All]
}] |>
]](https://www.wolframcloud.com/obj/resourcesystem/images/980/9808d3e0-eb5b-4acd-8981-74b86f648375/0e6a020a6dbdfb6d.png) |
| Out[11]= |
Define a training net with a learnable matrix:
| In[12]:= | ![trainingNet = NetGraph[
<|
"mat" -> NetArrayLayer[],
"sums" -> net,
"mse1" -> MeanSquaredLossLayer[],
"mse2" -> MeanSquaredLossLayer[]
|>,
{
"mat" -> "sums",
{NetPort["RowSums"], NetPort["sums", "RowSums"]} -> "mse1" -> NetPort["RowLoss"],
{NetPort["ColumnSums"], NetPort["sums", "ColumnSums"]} -> "mse2" -> NetPort["ColumnLoss"],
NetPort["sums", "SumOfSquares"] -> NetPort["SumOfSquaresLoss"]
}
]](https://www.wolframcloud.com/obj/resourcesystem/images/980/9808d3e0-eb5b-4acd-8981-74b86f648375/729a82012a0a3333.png) |
| Out[12]= |  |
Train the net to find a matrix with the given row and column sums:
| In[13]:= | ![input = <|"RowSums" -> {{5, 3, 2}}, "ColumnSums" -> { {1, 2, 3, 4}}|>;
trainedNet = NetTrain[trainingNet,
input,
LossFunction -> {"RowLoss", "ColumnLoss", "SumOfSquaresLoss"},
TimeGoal -> 10
]](https://www.wolframcloud.com/obj/resourcesystem/images/980/9808d3e0-eb5b-4acd-8981-74b86f648375/7a472d09fa7fab45.png) |
| Out[14]= | 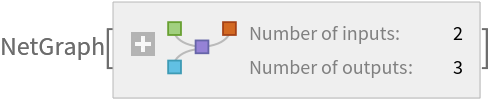 |
Extract the matrix found by the model:
| In[15]:= |
| Out[15]= |
Check the losses of the row and column deviations:
| In[16]:= |
| Out[16]= |
This work is licensed under a Creative Commons Attribution 4.0 International License