Basic Examples (1) 

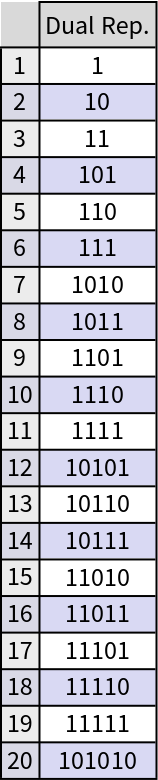
The dual Zeckendorf representation of first 20 integers (OEIS: A104326):

In[1]:=

Out[1]=

In[2]:=

Out[2]=

Scope (6) 

By definition, one can directly find dual Zeckendorf representation by eliminating binary string with "00":

In[3]:=

Out[3]=

Recover a number from its dual representation:

In[4]:=

Out[4]=

In[5]:=

Out[5]=

In[6]:=

Out[6]=

In[7]:=

Out[7]=

In the dual representation, the largest index of Fibonacci number has the following property:

In[8]:=

Out[9]=

In[10]:=

Out[10]=

Thus input falls precisely the gap between the sum of F_i for i = 2 to 28 and from 2 to 29=28+1:

In[11]:=

Out[11]=

The second largest value, 26, is found in the similar way by definition:

In[12]:=

Out[12]=

For any input n, its dual Zeckendorf representation is {1,1, … ,1} or zero-free if and only if n= F_k-2, where F_k is the k-th item in regular Fibonacci sequence with k>=4:

In[13]:=

Out[13]=

For any input n, its dual Zeckendorf representation is {1,0,1,0 … ,0|1} or alternating pattern (the ending in 0 or 1 depends on the parity of bit length) if and only if n= F_k-1, where F_k is the k-th item in regular Fibonacci sequence with k>=4:

In[14]:=

Out[14]=

On modern computers, it takes around 3 seconds to finding the dual Zeckendorf representation for the first 100K numbers:

In[15]:=

Out[16]=

Applications (2) 

Recover a Fibonacci number from the dual Zeckendorf representation by counting the number of k-bit vectors. For instance F(17)-2 = F(2)+F(3)+…+ F(15) where 15 = 17 -2:

In[17]:=

Out[17]=

In[18]:=

Out[18]=

Note that the numbers on the RHS of the rules are exactly the Fibonacci numbers:

In[19]:=

Out[19]=

This observation can be proved with a combinatorics argument.

Properties and Relations (3) 

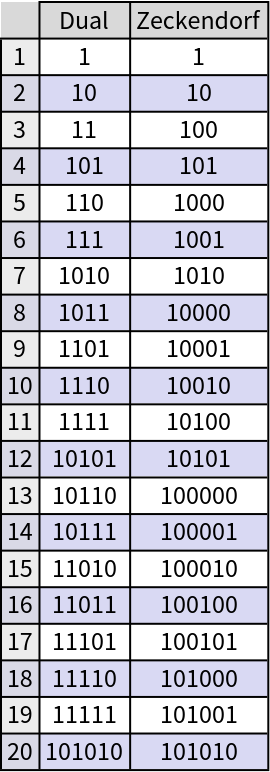
The dual Zeckendorf representation vs. Zeckendorf representation: the former does not allow consecutive zeros, meanwhile the latter does not allow consecutive ones. Check the fact with the first twenty numbers:

In[20]:=

In[21]:=

In[22]:=

Out[22]=

Fibonacci terms minus one:

In[23]:=

Out[23]=

The two representations for the numbers above 4, 7, 12, 20,… are identical:

In[24]:=

Out[24]=

Possible Issues (1) 

The input must be a positive integer. Otherwise the function returns unevaluated:

In[25]:=

Out[25]=

Neat Examples (4) 

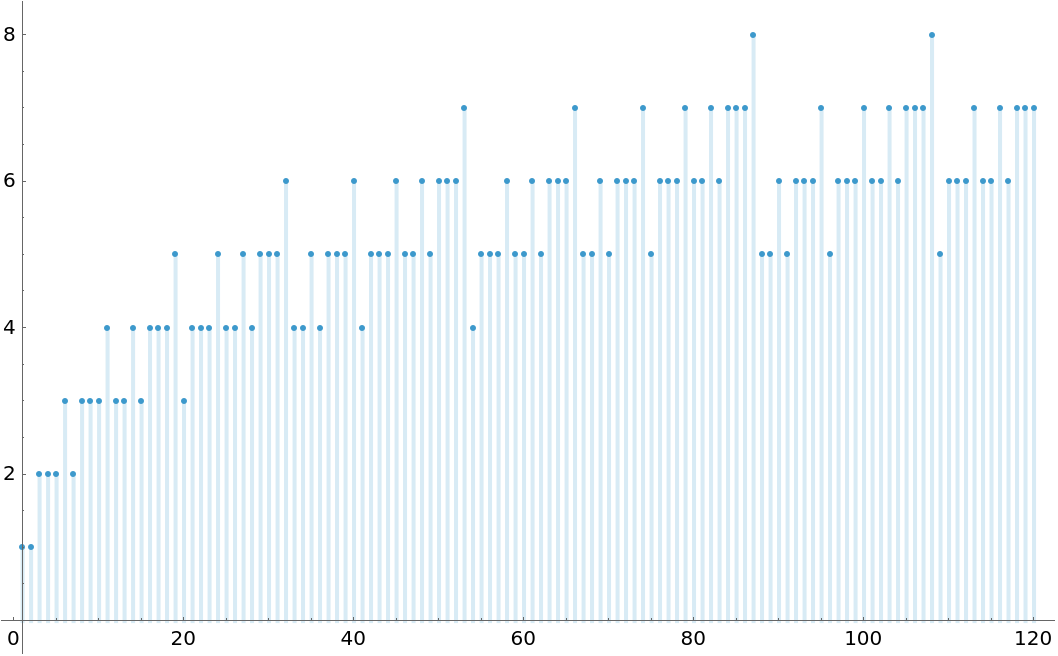
The number of ones in the dual Zeckendorf representation for first 120 numbers:

In[26]:=

Out[26]=

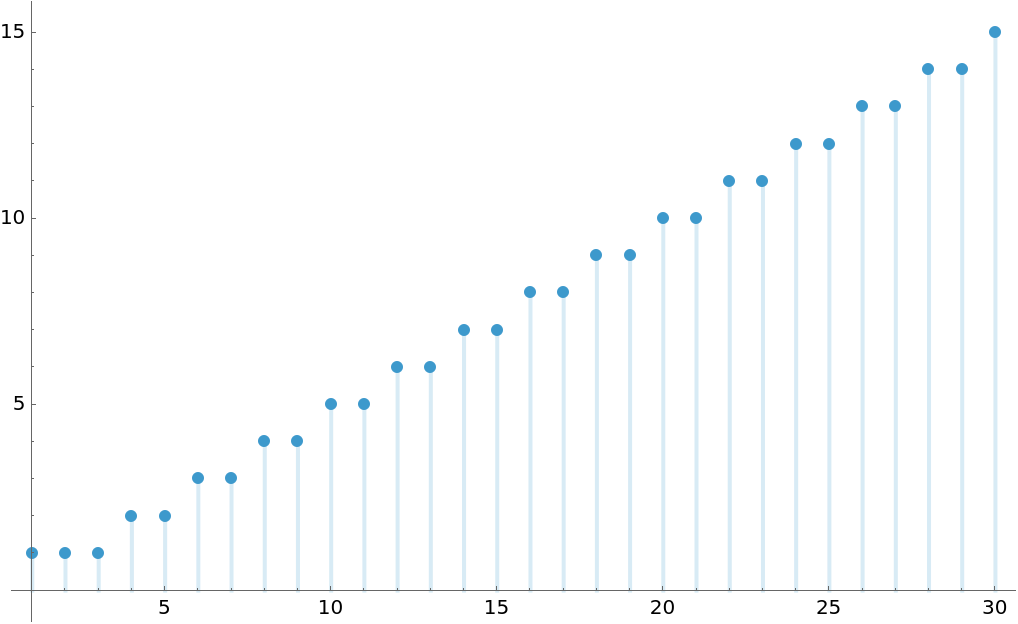
Compare the ones in the Zeckendorf and the dual representation for Fibonacci numbers:

In[27]:=

Out[27]=

In[28]:=

Out[28]=

Visualize the number of ones in the dual representation for Fibonacci number:

In[29]:=

Out[29]=

In[30]:=

Out[30]=

The sequence is OEIS A065033:

In[31]:=

Out[32]=

Because no consecutive zeros are allowed, all dual Zeckendorf representations are compact Huffman code:

In[33]:=

Out[33]=

In[34]:=

Out[34]=

This function can handle very large input:

In[35]:=

Out[36]=

Visualize the binary code with ArrayPlot:

In[37]:=

Out[37]=

Find the closed form for the average density of 1's in k-bit dual Zeckendorf representations as k approaches infinity:

In[38]:=

Out[38]=

In[39]:=

Out[39]=

The sum on the RHS of these rules has the following closed form expression (OEIS A023610):

In[40]:=

Out[41]=

In[42]:=

Out[42]=

Shift indices and find the limit as the bit length approaches infinity:

In[43]:=

Out[43]=

The result is simply (ϕ+2)/5 where ϕ is the golden ratio (use Binet's formula and ϕ²=ϕ+1 for proof):

In[44]:=

Out[44]=