Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Compute the intercepts of a function with the coordinate axes
ResourceFunction["Intercepts"][expr,{x,y,…}] finds the intercepts of the expression expr with respect to the axis variables x,y,…. | |
ResourceFunction["Intercepts"][expr,var,x] returns only the x intercepts of the graph of expr. |
Find the intercepts of a line:
| In[1]:= |
| Out[1]= |
| In[2]:= |
| Out[2]= | 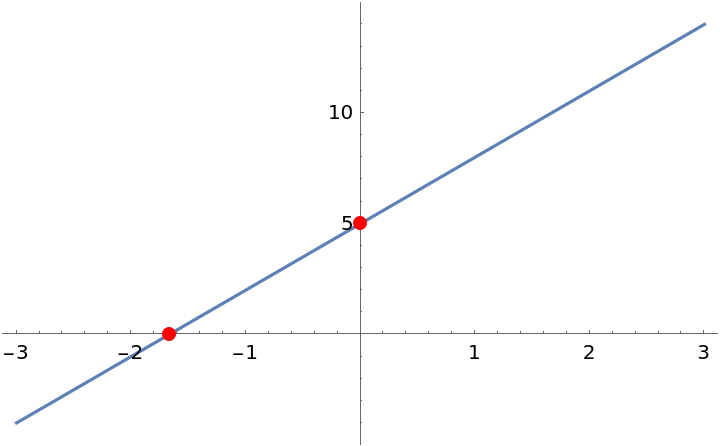 |
Find the intercepts of a parabola:
| In[3]:= |
| Out[3]= |
| In[4]:= | ![Plot[x^2 + 2 x - 3, {x, -4, 2.5}, Epilog -> Join[{Red, PointSize@Large}, Point /@ Flatten[Values[%], {1}]]
]](https://www.wolframcloud.com/obj/resourcesystem/images/95c/95cdfff4-26f4-46a1-8cc8-5ce268e7ebfd/30dc5b16a3eb15d2.png) |
| Out[4]= | 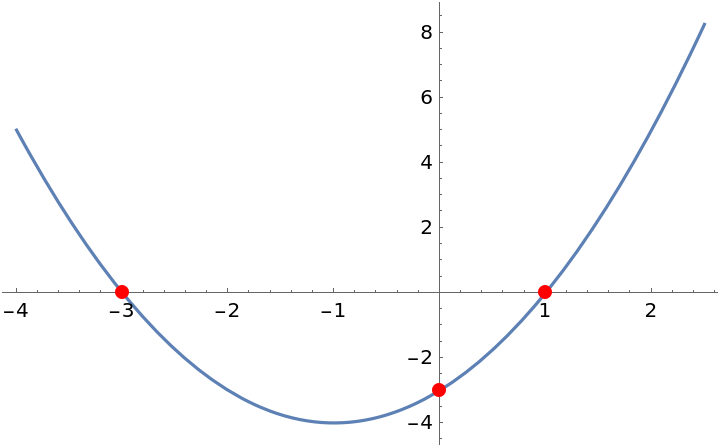 |
Find the intercepts of an implicitly defined circle:
| In[5]:= |
| Out[5]= |
| In[6]:= | ![Plot[{0.3 + Sqrt[9 - (x - 1.75)^2], 0.3 - Sqrt[9 - (x - 1.75)^2]}, {x, -5, 5}, Epilog -> Join[{Red, PointSize@Large}, Point /@ Flatten[Values[%], {1}]]
]](https://www.wolframcloud.com/obj/resourcesystem/images/95c/95cdfff4-26f4-46a1-8cc8-5ce268e7ebfd/1bcb5478545344c4.png) |
| Out[6]= | 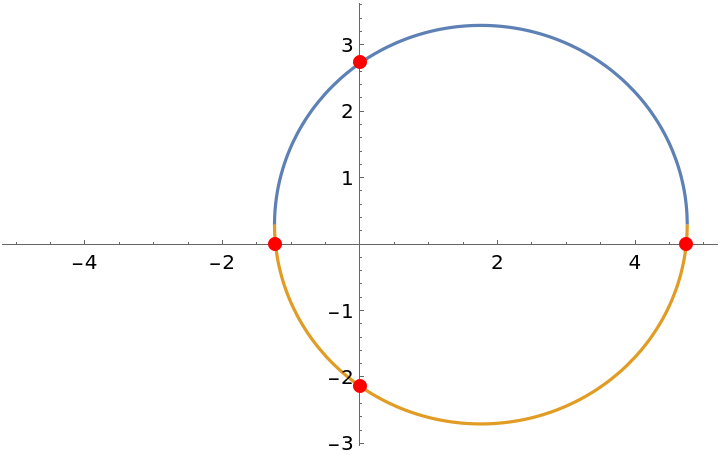 |
Intercepts[expr,…] can handle the use of symbolic parameters in expr:
| In[7]:= |
| Out[7]= |
Use the "Constraints" option to restrict the results returned:
| In[8]:= |
| Out[8]= |
With the default setting "Constraints"→True, all results are included:
| In[9]:= |
| Out[9]= |
This work is licensed under a Creative Commons Attribution 4.0 International License