Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 StrictIntegerCompositions

Source Notebook

Generate the zero-free compositions of a positive integer

Contributed by: Wolfram Staff

ResourceFunction["StrictIntegerCompositions"][n]

gives a list of all possible ways to form a composition of the integer n into smaller integers.

ResourceFunction["StrictIntegerCompositions"][n,k]

gives compositions using at most k integers.

ResourceFunction["StrictIntegerCompositions"][n,{k}]

gives compositions into exactly k integers.

ResourceFunction["StrictIntegerCompositions"][n,{kmin,kmax}]

gives compositions into between kmin and kmax integers.

ResourceFunction["StrictIntegerCompositions"][n,kspec,{s1,s2,…}]

gives compositions involving only the numbers si.

ResourceFunction["StrictIntegerCompositions"][n,kspec,sspec,m]

limits the result to using only first m partitions.

Details and Options

ResourceFunction["StrictIntegerCompositions"] includes all possible permutations of compositions given by IntegerPartitions.
ResourceFunction["StrictIntegerCompositions"][n] is equivalent to ResourceFunction["StrictIntegerCompositions"][n,All].
ResourceFunction["StrictIntegerCompositions"][n,{kmin,kmax,dk}] gives compositions into kmin, kmin+dk, … integers.
n and the si can be rational numbers, and can be negative.
In the list of compositions, those involving earlier si are given last.
In ResourceFunction["StrictIntegerCompositions"][n,kspec,sspec,m], a kspec of All corresponds to {0,Infinity}, an sspec of All corresponds to Range[n] and an m of All corresponds to Infinity.

Examples

Basic Examples (1) 

All the strict compositions of an integer:

In[1]:=
ResourceFunction["StrictIntegerCompositions"][4]
Out[1]=

Scope (6) 

All the strict compositions of 5:

In[2]:=
ResourceFunction["StrictIntegerCompositions"][5]
Out[2]=

The compositions of 5 into at most three integers:

In[3]:=
ResourceFunction["StrictIntegerCompositions"][5, 3]
Out[3]=

Compositions that involve only 1, 2 and 4:

In[4]:=
ResourceFunction["StrictIntegerCompositions"][5, All, {1, 2, 4}]
Out[4]=

Compositions of even length only:

In[5]:=
ResourceFunction["StrictIntegerCompositions"][5, {2, Infinity, 2}]
Out[5]=

Ways to form 3 from any of five given rational numbers:

In[6]:=
ResourceFunction["StrictIntegerCompositions"][3, 5, {1, 1/3, 3/4}]
Out[6]=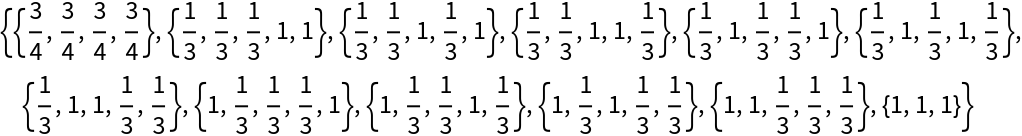

Limit the number of results:

In[7]:=
ResourceFunction["StrictIntegerCompositions"][6, All, All, 7]
Out[7]=

Properties and Relations (5) 

There are 2n-1 strict compositions of n:

In[8]:=
n = 5;
In[9]:=
ResourceFunction["StrictIntegerCompositions"][5]
Out[9]=
In[10]:=
Length[%]
Out[10]=
In[11]:=
2^(n - 1)
Out[11]=

Each composition adds up to the original number:

In[12]:=
ResourceFunction["StrictIntegerCompositions"][4]
Out[12]=
In[13]:=
Total /@ %
Out[13]=

StrictIntegerCompositions gives the permutations of compositions returned by IntegerPartitions:

In[14]:=
compositions = ResourceFunction["StrictIntegerCompositions"][4]
Out[14]=
In[15]:=
partitions = IntegerPartitions[4]
Out[15]=
In[16]:=
Union[Sort /@ compositions] === Sort /@ partitions
Out[16]=

Results of StrictIntegerCompositions do not include zeros, whereas results of the resource function IntegerCompositions do:

In[17]:=
ResourceFunction["StrictIntegerCompositions"][4, 2]
Out[17]=
In[18]:=
ResourceFunction["IntegerCompositions"][4, 2]
Out[18]=

Unlike the resource function IntegerCompositions, StrictIntegerCompositions does not necessarily give compositions in canonical order:

In[19]:=
strict = ResourceFunction["StrictIntegerCompositions"][5, 3]
Out[19]=
In[20]:=
all = ResourceFunction["IntegerCompositions"][5, 3]
Out[20]=
In[21]:=
(Sort[#] === #) & /@ {strict, all}
Out[21]=

Possible Issues (3) 

StrictIntegerCompositions cannot give an infinite list of compositions:

In[22]:=
ResourceFunction["StrictIntegerCompositions"][5, All, {1, -1}]
Out[22]=

Get a finite list instead:

In[23]:=
ResourceFunction["StrictIntegerCompositions"][5, 8, {1, -1}]
Out[23]=

There are no strict compositions of 1/2:

In[24]:=
ResourceFunction["StrictIntegerCompositions"][1/2]
Out[24]=

There are, however, compositions into rationals:

In[25]:=
ResourceFunction["StrictIntegerCompositions"][1/2, All, {1/6, 1/3}]
Out[25]=

If all items requested by the fourth argument are not present, as many as possible are returned:

In[26]:=
ResourceFunction["StrictIntegerCompositions"][3, All, All, 7]
Out[26]=

Neat Examples (1) 

A compact way to show integer compositions:

In[27]:=
Row /@ ResourceFunction["StrictIntegerCompositions"][5]
Out[27]=

Version History

  • 1.0.0 – 06 March 2020

Related Resources

License Information