Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Represent a non-negative integer as the sum of three binomial coefficients
Find the binomial number representation for the first twenty integers:
| In[1]:= |
| Out[1]= |
Find the binomial number representation for a larger non-negative integer:
| In[2]:= |
| Out[2]= |
Verify that the following sum gives back the original input:
| In[3]:= |
| Out[3]= |
By determining a tight bound for each item in the triplet before initiating the solution search, the internal algorithm allows the function to process large inputs efficiently:
| In[4]:= |
| Out[4]= |  |
| In[5]:= |
| Out[5]= |
There is a unique representation for zero:
| In[6]:= |
| Out[6]= |
It is based on the fact that Binomial[n,k] vanishes for integers n and k such that n<k:
| In[7]:= |
| Out[7]= |
For those input values exactly equal to Binomial[k,3], the returned triplets always begin with a=0 and b=1:
| In[8]:= |
| Out[8]= |
For integers from 1 to n, the subsequence formed by numbers with a=1 in the binomial number representation is OEIS A126862:
| In[9]:= |
| Out[9]= |  |
| In[10]:= |
| Out[10]= |  |
The ResourceFunction SubsetFromIndex uses a similar algorithm:
| In[11]:= |
| Out[11]= |
| In[12]:= |
| Out[12]= |
The input must be a non-negative integer. Otherwise the function returns unevaluated:
| In[13]:= |
| Out[13]= |
The uniqueness of the representation is lost if {a,b,c} is not strictly increasing:
| In[14]:= |
| Out[14]= |
Imposing the order ensures that the solution is unique. For instance:
| In[15]:= |
| Out[15]= |
| In[16]:= |
| Out[16]= |
Visualize the "digit sum" of the binomial number representation for some non-negative integers:
| In[17]:= | ![ListPlot[
Total[ResourceFunction["BinomialNumberSystemTriplet"] /@ Range[Binomial[17, 3] - 1], {2}], PlotHighlighting -> None]](https://www.wolframcloud.com/obj/resourcesystem/images/94c/94c16978-64d6-4c1b-9b58-aabd572c3800/049aca1790a5279b.png) |
| Out[17]= | 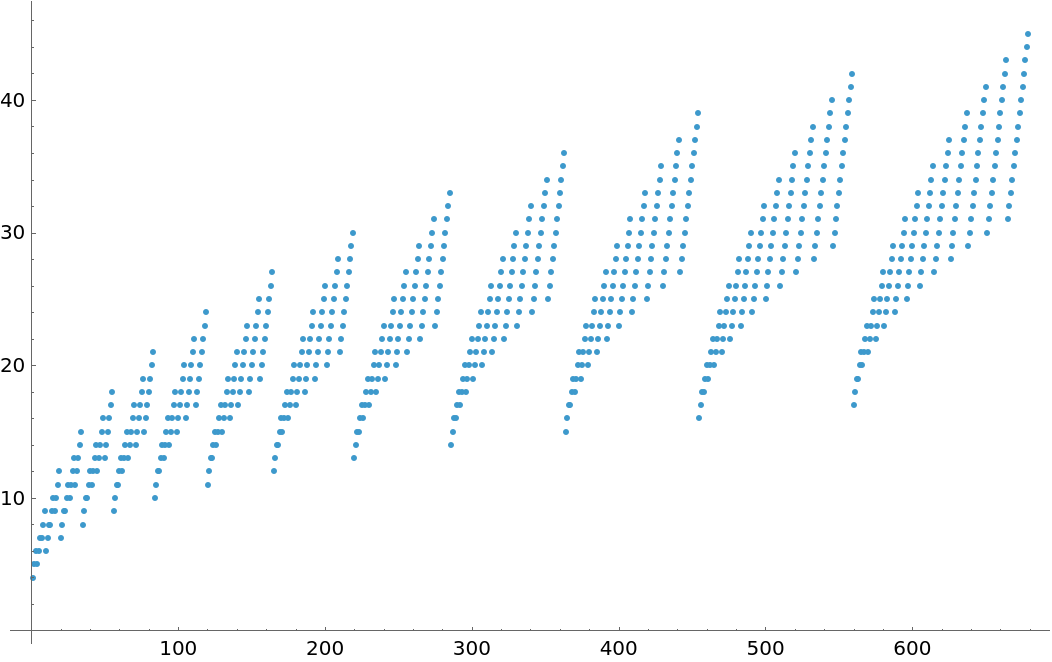 |
A graphic for the progression of triples:
| In[18]:= |
| Out[18]= | 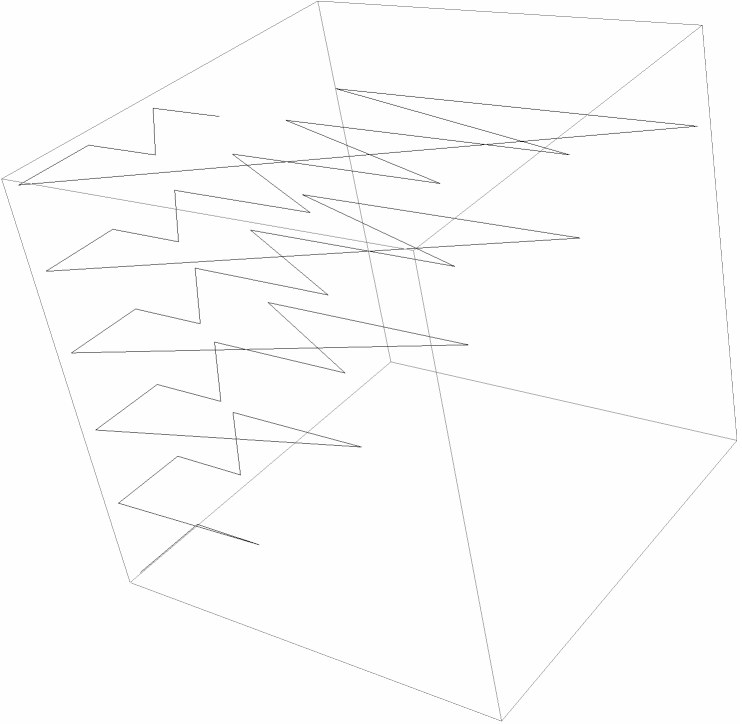 |
This work is licensed under a Creative Commons Attribution 4.0 International License