Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 KnuthBendixCompletion

Source Notebook

Compute the Knuth-Bendix completion for a given multiway system

Contributed by: Jonathan Gorard

ResourceFunction["KnuthBendixCompletion"][rules,init,n]

generates a list of Knuth-Bendix completion rules for the multiway system with the specified rules after n steps, starting with initial conditions init.

ResourceFunction["KnuthBendixCompletion"][rules→sel,init,n]

uses the function sel to select which of the events obtained at each step to include in the evolution.

Details and Options

Rules can be specified in the following ways:
{"lhs1"->"rhs1",…}string substitution system
{{l11,l12,…}->{r11,r12,..},…}list substitution system
WolframModel[rules]Wolfram Model system
CellularAutomaton[rules]cellular automaton system
"type"→rulessystem of the specified type
Supported rule types include:
"StringSubstitutionSystem"rules given as replacements on strings
"ListSubstitutionSystem"rules given as replacements on lists
"CellularAutomaton"rules given as a list of CellularAutomaton rule specifications
"WolframModel"rules given as replacements on hypergraphs
When rules are specified by an explicit association, the following elements can be included:
"StateEvolutionFunction"gives the list of successors to a given state
"StateEquivalenceFunction"determines whether two states should be considered equivalent
"StateEventFunction"gives the list of events applicable to a given state
"EventApplicationFunction"applies an event to a given state
"EventDecompositionFunction"decomposes an event into creator and destroyer events for individual elements
"SystemType"system type name
"EventSelectionFunction"determines which events should be applied to a given state
The event selection function sel in ResourceFunction["KnuthBendixCompletion"][rules→sel,…] can have the following special forms:
"Sequential"applies the first possible replacement (sequential substitution system)
"Random"applies a random replacement
{"Random",n}applies n randomly chosen replacements
"MaxScan"applies the maximal set of spatially-separated replacements (strings only)
The initial condition for ResourceFunction["KnuthBendixCompletion"] is a list of states appropriate for the type of system used.
ResourceFunction["KnuthBendixCompletion"][rules,"string",…] is interpreted as ResourceFunction["KnuthBendixCompletion"][rules,{"string"},…].
ResourceFunction["KnuthBendixCompletion"] accepts both individual rules and lists of rules, and likewise for initial conditions.
Options for ResourceFunction["KnuthBendixCompletion"] include:
"IncludeStepNumber"Falsewhether to label states and events with their respective step numbers
"IncludeStateID"Falsewhether to label states and events with unique IDs
Knuth-Bendix completion transforms an arbitrary rewrite system into a confluent (causal invariant) rewrite system by resolving critical pairs.
In the context of the multiway systems, critical (branch) pairs indicate bifurcations or ambiguities in the multiway evolution.
ResourceFunction["KnuthBendixCompletion"] gives the minimal set of rules required to force all unresolved branch pairs to converge.

Examples

Basic Examples (4) 

Generate the list of all Knuth-Bendix completion rules for two string substitution systems:

In[1]:=
ResourceFunction[ "KnuthBendixCompletion"][{"AA" -> "ABA", "AAA" -> "B"}, "AAA", 2]
Out[1]=
In[2]:=
ResourceFunction[ "KnuthBendixCompletion"][{"AA" -> "AB", "B" -> "BA"}, "AABAA", 2]
Out[2]=

Different event selection functions can lead to different lists of Knuth-Bendix completion rules:

In[3]:=
ResourceFunction[ "KnuthBendixCompletion"][{"AA" -> "ABA", "AAA" -> "B"}, "AAA", 2]
Out[3]=
In[4]:=
ResourceFunction[ "KnuthBendixCompletion"][{"AA" -> "ABA", "AAA" -> "B"} -> "Sequential", "AAA", 2]
Out[4]=

KnuthBendixCompletion can handle Wolfram models and other system types:

In[5]:=
ResourceFunction["KnuthBendixCompletion"][ "WolframModel" -> {{{2, 2, 1}, {2, 2, 2}} -> {{1, 1, 3}, {3, 3, 2}}}, {{{2, 2, 1}, {2, 2, 3}, {2, 2, 2}, {3, 3, 3}}}, 1]
Out[5]=

Provide a cellular automaton as input:

In[6]:=
ResourceFunction["KnuthBendixCompletion"][ CellularAutomaton[30], {0, 0, 1, 0, 0}, 2]
Out[6]=

Preventing identical states from being merged, by including step numbers and/or state IDs, can change the resulting Knuth-Bendix completions:

In[7]:=
ResourceFunction[ "KnuthBendixCompletion"][{"AA" -> "AB", "B" -> "BA"}, "AABAA", 2]
Out[7]=
In[8]:=
ResourceFunction[ "KnuthBendixCompletion"][{"AA" -> "AB", "B" -> "BA"}, "AABAA", 2, "IncludeStepNumber" -> True, "IncludeStateID" -> True]
Out[8]=

Scope (13) 

System Types (8) 

KnuthBendixCompletion supports both string and list substitution systems:

In[9]:=
ResourceFunction[ "KnuthBendixCompletion"][{"BB" -> "AA", "AB" -> "BA"}, "ABBA", 2]
Out[9]=

Use substitutions on lists:

In[10]:=
ResourceFunction[ "KnuthBendixCompletion"][{{1, 1} -> {0, 0}, {0, 1} -> {1, 0}}, {0, 1, 1, 0}, 2]
Out[10]=

Lists can contain arbitrary symbolic elements:

In[11]:=
(* Evaluate this cell to get the example input *) CloudGet["https://www.wolframcloud.com/obj/8a339292-802c-4510-9838-2e8b3981098f"]
Out[11]=

Give an explicit substitution system rule:

In[12]:=
ResourceFunction["KnuthBendixCompletion"][ SubstitutionSystem[{{0} -> {0, 0}, {0} -> {0, 1}}], {{0}}, 3]
Out[12]=

An alternative method of specifying that a substitution system should be used:

In[13]:=
ResourceFunction["KnuthBendixCompletion"][ "SubstitutionSystem" -> {{0} -> {0, 0}, {0} -> {0, 1}}, {{0}}, 3]
Out[13]=

KnuthBendixCompletion also supports multiway generalizations of cellular automata:

In[14]:=
ResourceFunction["KnuthBendixCompletion"][ CellularAutomaton[{170, 240}], {0, 0, 1, 0, 0}, 1]
Out[14]=

Generate a Knuth-Bendix completion for left- and right-shift cellular automaton rules after 3 steps:

In[15]:=
ResourceFunction["KnuthBendixCompletion"][ CellularAutomaton[{170, 240}], {0, 0, 1, 0, 0}, 3]
Out[15]=

Determine that the rule 30 cellular automaton is not causal invariant:

In[16]:=
ResourceFunction["KnuthBendixCompletion"][ CellularAutomaton[30], {0, 0, 1, 0, 0}, 2]
Out[16]=

KnuthBendixCompletion also supports multiway generalizations of Wolfram Models:

In[17]:=
ResourceFunction["KnuthBendixCompletion"][ "WolframModel" -> {{{0, 1}, {1, 0}} -> {{1, 2}, {2, 1}, {0, 1}}}, {{{0, 1}, {1, 0}, {0, 1}, {2, 3}}}, 1]
Out[17]=
In[18]:=
ResourceFunction["KnuthBendixCompletion"][ "WolframModel" -> {{{0, 1}} -> {{1, 2}, {2, 1}}}, {{{0, 1}, {1, 0}}}, 1]
Out[18]=

Construct a multiway evolution by explicitly specifying an association:

In[19]:=
ResourceFunction[ "KnuthBendixCompletion"][<| "StateEvolutionFunction" -> (StringReplaceList[#, {"A" -> "AA", "B" -> "AB"}] &), "StateEquivalenceFunction" -> SameQ, "StateEventFunction" -> Identity, "EventDecompositionFunction" -> Identity, "EventApplicationFunction" -> Identity, "SystemType" -> "None", "EventSelectionFunction" -> Identity|>, {"ABA"}, 3]
Out[19]=

Rules and Initial Conditions (2) 

KnuthBendixCompletion accepts both individual rules and lists of rules:

In[20]:=
ResourceFunction["KnuthBendixCompletion"]["A" -> "AA", "AAA", 1]
Out[20]=
In[21]:=
ResourceFunction[ "KnuthBendixCompletion"][{"A" -> "AB", "B" -> "BA"}, "AAABA", 1]
Out[21]=

Likewise for initial conditions:

In[22]:=
ResourceFunction[ "KnuthBendixCompletion"][{"A" -> "AB", "B" -> "BA"}, {"ABA", "AAB"}, 2]
Out[22]=

Event Selection Functions (3) 

Apply only the first possible event at each step:

In[23]:=
ResourceFunction[ "KnuthBendixCompletion"][{"A" -> "AAB", "BA" -> "A"} -> "Sequential", "A", 2]
Out[23]=

Apply the first and last possible events at each step:

In[24]:=
ResourceFunction[ "KnuthBendixCompletion"][{"A" -> "AAB", "BA" -> "A"} -> ({First[#], Last[#]} &), "ABA", 1]
Out[24]=

Use a greedy-style algorithm to apply the maximal set of non-conflicting events at each step (strings only):

In[25]:=
ResourceFunction[ "KnuthBendixCompletion"][{"A" -> "AA", "BA" -> "AB"} -> "MaxScan", "ABA", 4]
Out[25]=

Options (3) 

Explicitly specify the type of rule:

In[26]:=
ResourceFunction["KnuthBendixCompletion"][ "SubstitutionSystem" -> {"A" -> "AA", "A" -> "AB"}, {"ABA"}, 2]
Out[26]=
In[27]:=
ResourceFunction["KnuthBendixCompletion"][ "SubstitutionSystem" -> {{0} -> {0, 0}, {0} -> {0, 1}}, {{0, 1, 0}}, 2]
Out[27]=

Step Numbers and State IDs (3) 

By default, equivalent states are merged across all time steps:

In[28]:=
ResourceFunction[ "KnuthBendixCompletion"][{"A" -> "AB", "B" -> "BA"}, {"BABB"}, 1]
Out[28]=

Merging of equivalent states across different time steps can be prevented by including step numbers:

In[29]:=
ResourceFunction[ "KnuthBendixCompletion"][{"A" -> "AB", "B" -> "BA"}, {"BABB"}, 1, "IncludeStepNumber" -> True]
Out[29]=

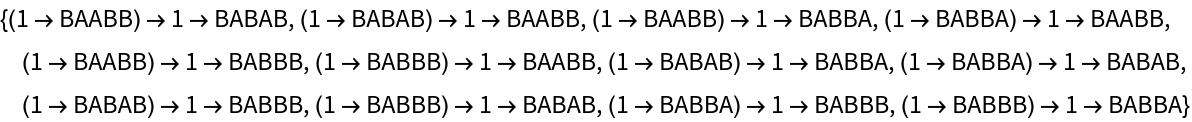
Merging of equivalent states at the same time step can be prevented by also including state IDs:

In[30]:=
ResourceFunction[ "KnuthBendixCompletion"][{"A" -> "AB", "B" -> "BA"}, {"BABB"}, 1, "IncludeStepNumber" -> True, "IncludeStateID" -> True]
Out[30]=

Applications (2) 

Causal Invariant Rules (2) 

Prove that the Xor and And functions are causal invariant (due to associativity):

In[31]:=
ResourceFunction[ "KnuthBendixCompletion"][{"TT" -> "F", "TF" -> "T", "FT" -> "T", "FF" -> "F"}, "TFTTFF", 5]
Out[31]=
In[32]:=
ResourceFunction[ "KnuthBendixCompletion"][{"TT" -> "T", "TF" -> "F", "FT" -> "F", "FF" -> "F"}, "TFTTFF", 5]
Out[32]=

On the other hand, the Nand function is not associative, so it is not total causal invariant:

In[33]:=
ResourceFunction[ "KnuthBendixCompletion"][{"TT" -> "F", "TF" -> "T", "FT" -> "T", "FF" -> "T"}, "TFTTFF", 5]
Out[33]=

Properties and Relations (1) 

KnuthBendixCompletion returning an empty list of Knuth-Bendix completion rules is a sufficient (but not necessary) condition for causal invariance:

In[34]:=
ResourceFunction[ "KnuthBendixCompletion"][{"TT" -> "F", "TF" -> "T", "FT" -> "T", "FF" -> "T"}, "TFTTFF", 5]
Out[34]=
In[35]:=
ResourceFunction[ "KnuthBendixCompletion"][{"TT" -> "F", "TF" -> "T", "FT" -> "T", "FF" -> "F"}, "TFTTFF", 5]
Out[35]=

Version History

  • 1.0.0 – 13 April 2020

Source Metadata

  • Citation:
    • Stephen Wolfram (2002), “A New Kind of Science”
    • Stephen Wolfram (2020), “A Class of Models with Potential to Represent Fundamental Physics”
    • Jonathan Gorard (2020), “Some Relativistic and Gravitational Properties of the Wolfram Model”
    • Jonathan Gorard (2020), “Some Quantum Mechanical Properties of the Wolfram Model”

Related Resources

License Information