Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Compute the Gaussian curvature of a surface
ResourceFunction["GaussianCurvature"][s,{u,v}] computes the Gaussian curvature of the surface s parameterized by u and v. | |
ResourceFunction["GaussianCurvature"][eq,{x,y,z}] computes the Gaussian curvature of the surface s given by the implicit equation eq in variables x,y and z. |
Compute the Gaussian curvature of a sphere:
| In[1]:= |
| Out[1]= |
Plot an astroidal ellipsoid:
| In[2]:= | ![ParametricPlot3D[
Evaluate[
Entity["Surface", "AstroidalEllipsoid"]["ParametricEquations"][1, 1,
1][u, v]], {u, 0, 2 \[Pi]}, {v, -(\[Pi]/2), \[Pi]/2}, PlotPoints -> 50, PlotRange -> 1]](https://www.wolframcloud.com/obj/resourcesystem/images/8f7/8f739cf2-ab2b-4fab-bf6e-34e4ac65627f/5d385aa078d7c699.png) |
| Out[2]= | 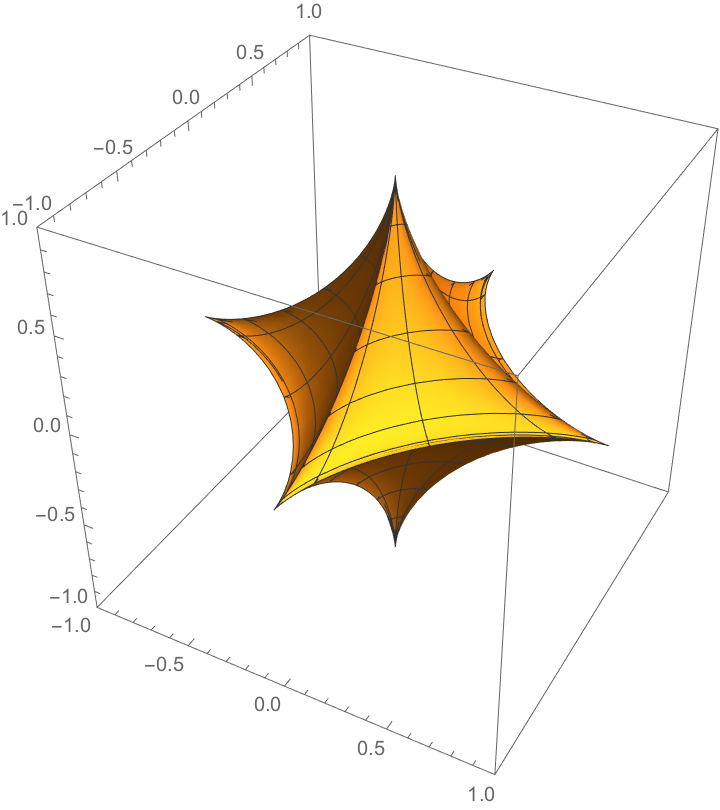 |
Now compute its Gaussian curvature:
| In[3]:= | ![ResourceFunction["GaussianCurvature"][
Entity["Surface", "AstroidalEllipsoid"]["ParametricEquations"][a, b, c][u, v], {u, v}]](https://www.wolframcloud.com/obj/resourcesystem/images/8f7/8f739cf2-ab2b-4fab-bf6e-34e4ac65627f/646bae200ea48b2a.png) |
| Out[3]= |
Plot the Gaussian curvature:
| In[4]:= | ![Plot3D[Evaluate[
ResourceFunction["GaussianCurvature"][
Entity["Surface", "AstroidalEllipsoid"]["ParametricEquations"][1, 1, 1][u, v], {u, v}]], {u, 0, 2 \[Pi]}, {v, -(\[Pi]/2), \[Pi]/2},
PlotRange -> {{0, 2 \[Pi]}, {-(\[Pi]/2), \[Pi]/2}, {0, 150}}, PlotPoints -> 50]](https://www.wolframcloud.com/obj/resourcesystem/images/8f7/8f739cf2-ab2b-4fab-bf6e-34e4ac65627f/712969ef6aae1616.png) |
| Out[4]= | 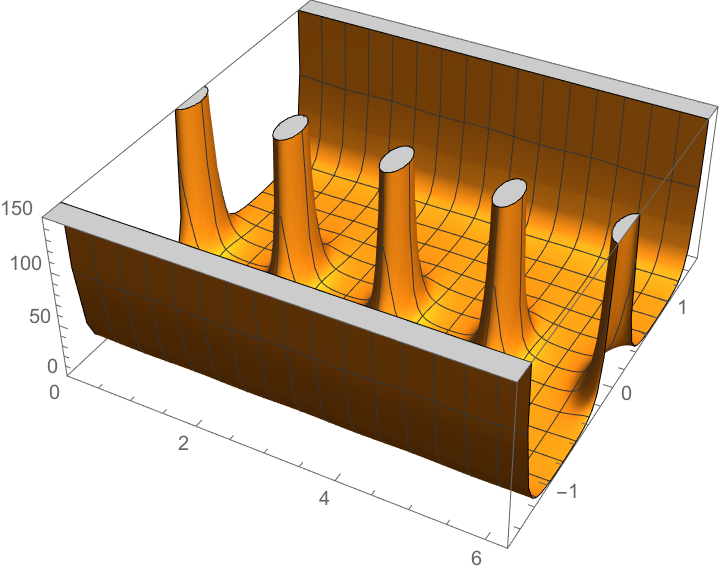 |
Define a Möbius strip:
| In[5]:= |
| Out[5]= |
Compute the Gaussian curvature:
| In[6]:= |
| Out[6]= |
Plot the Gaussian curvature:
| In[7]:= |
| Out[7]= | 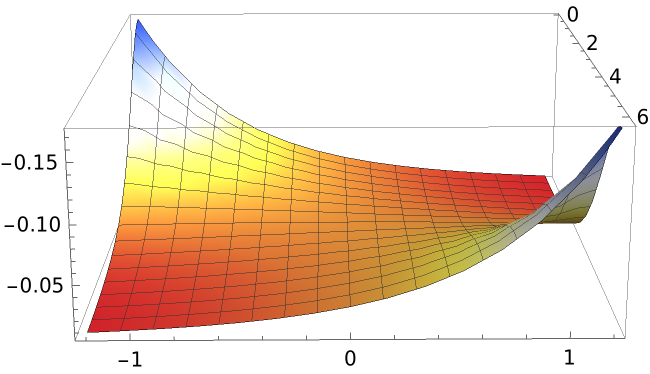 |
Plot the Möbius strip colored according to its Gaussian curvature:
| In[8]:= | ![range = Last[
PlotRange /. AbsoluteOptions[curp, PlotRange]]; ParametricPlot3D[mobius, {u, -1.2, 1.2}, {v, 0, 2 Pi}, PlotRange -> All, Boxed -> False, PlotStyle -> Opacity[0.8], PlotPoints -> {80, 20}, Mesh -> 12, MeshFunctions -> Function[{x, y, z, u, v}, Rescale[gcur, range]], ColorFunction -> Function[{x, y, z, u, v}, ColorData["TemperatureMap"][Rescale[gcur, range]]], ColorFunctionScaling -> False]](https://www.wolframcloud.com/obj/resourcesystem/images/8f7/8f739cf2-ab2b-4fab-bf6e-34e4ac65627f/500845145363f059.png) |
| Out[8]= | 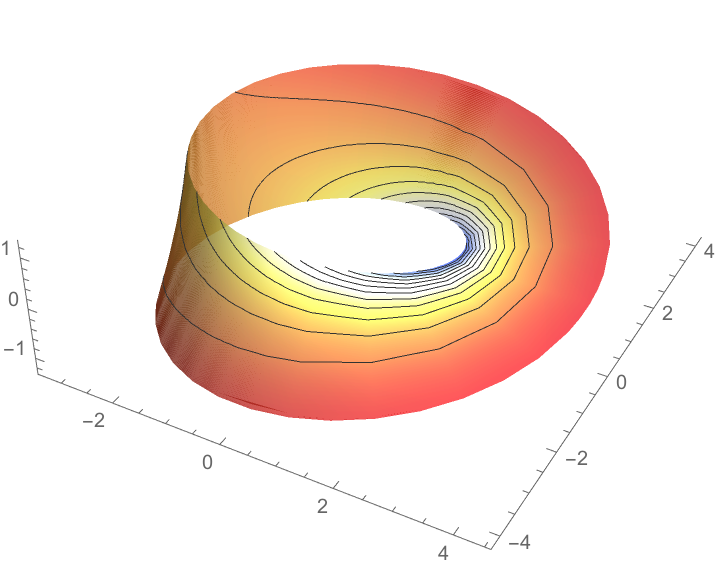 |
Here is an implicit equation for a surface:
| In[9]:= |
Plot it:
| In[10]:= |
| Out[10]= | 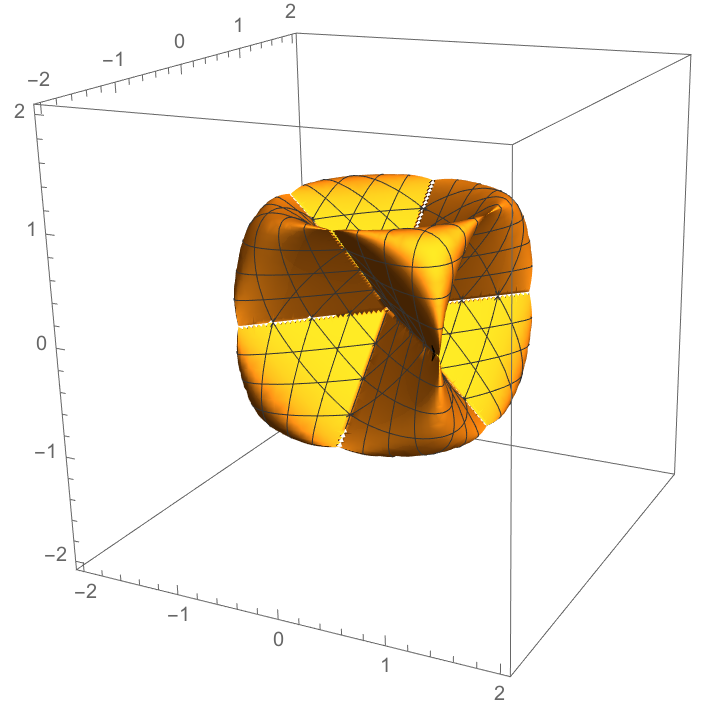 |
Compute its Gaussian curvature:
| In[11]:= |
| Out[11]= | 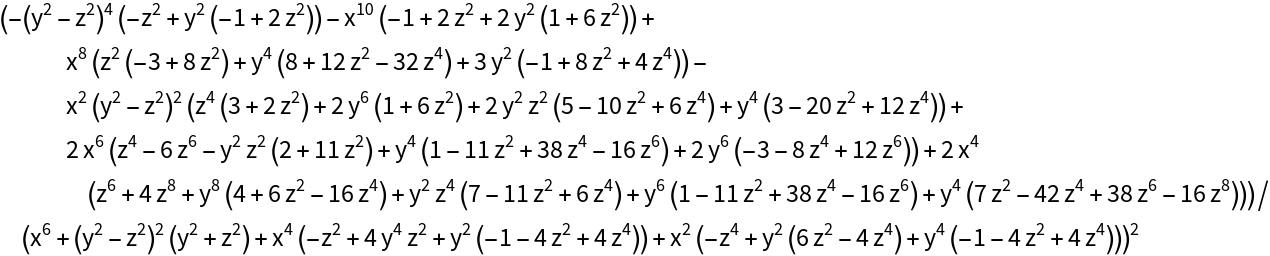 |
The curvature can be obtained for named surfaces using entities:
| In[12]:= |
| Out[12]= |
Here is the result returned by GaussianCurvature:
| In[13]:= | ![ResourceFunction["GaussianCurvature"][
Entity["Surface", "AstroidalEllipsoid"]["ParametricEquations"][a, b, c][u, v], {u, v}]](https://www.wolframcloud.com/obj/resourcesystem/images/8f7/8f739cf2-ab2b-4fab-bf6e-34e4ac65627f/0f6723683fcee235.png) |
| Out[13]= |
The expressions seem to be different, but they are equal:
| In[14]:= | ![FullSimplify[
Entity["Surface", "AstroidalEllipsoid"][
EntityProperty["Surface", "GaussianCurvature"]][a, b, c][u, v] - ResourceFunction["GaussianCurvature"][
Entity["Surface", "AstroidalEllipsoid"]["ParametricEquations"][a, b, c][u, v], {u, v}]]](https://www.wolframcloud.com/obj/resourcesystem/images/8f7/8f739cf2-ab2b-4fab-bf6e-34e4ac65627f/5ff4400560d2e9e7.png) |
| Out[14]= |
This work is licensed under a Creative Commons Attribution 4.0 International License