Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 EulerianNumberTriangle

Source Notebook

Construct a Pascal-like triangular graph representing Eulerian numbers

Contributed by: Shenghui Yang

ResourceFunction["EulerianNumberTriangle"][n]

constructs a triangle that encodes the Eulerian numbers arranged in n+1 layers with edge weights.

Details

This is a variation of the better known Pascal triangle with values multiplied by edge weights before being added together.
EulerianNumberTriangle returns a weighted Graph object.
The Eulerian number A(n,k) gives the number of permutations of {1,2,…,n} having k permutation ascents.
The Eulerian numbers A(n,k) satisfy the recurrence relation: A(n,k) = (n-k+1)A(n-1)+k A(n-1,k) with A(1,1)=1.
When numbers are greater than 1000, they are shown in format with a mouseover needed to show the number.

Examples

Basic Examples (1) 

Generate an Eulerian number triangle with 6 levels:

In[1]:=
ResourceFunction["EulerianNumberTriangle"][5]
Out[1]=

Scope (1) 

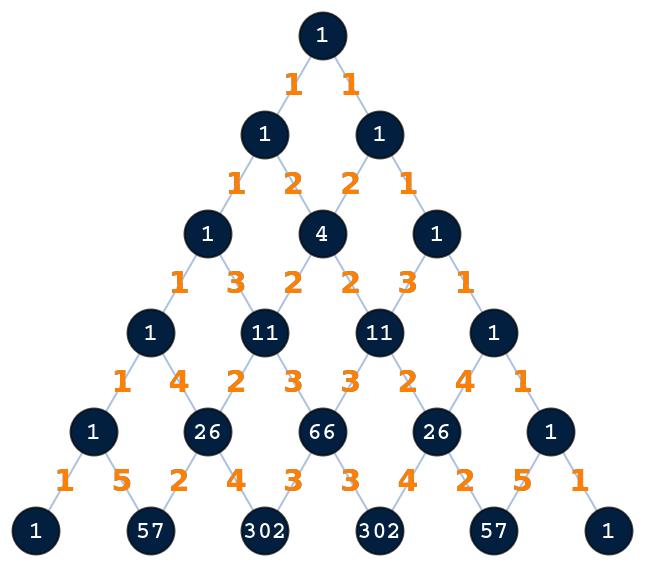Mouse over to display Eulerian numbers larger than 1000:

In[2]:=
ResourceFunction["EulerianNumberTriangle"][6]
Out[2]=

Properties and Relations (3) 

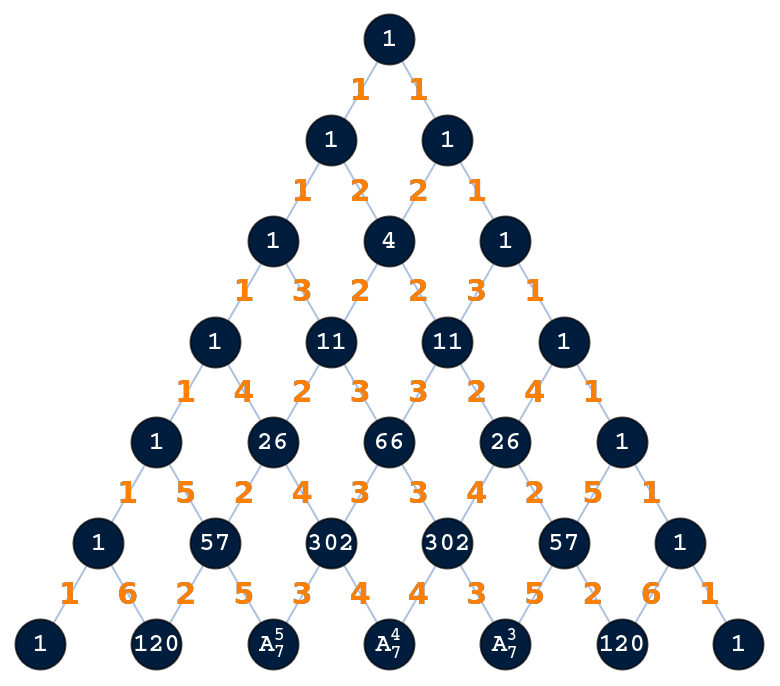EulerianNumberTriangle returns a weighed Graph object:

In[3]:=
g = ResourceFunction["EulerianNumberTriangle"][5]; {Head[g], EdgeWeightedGraphQ[g]}
Out[4]=

Each value in the node is the weighted sum of the parent items, for example, 26 = 4·1+11·2:

In[5]:=
ResourceFunction["EulerianNumberTriangle"][6]
Out[5]=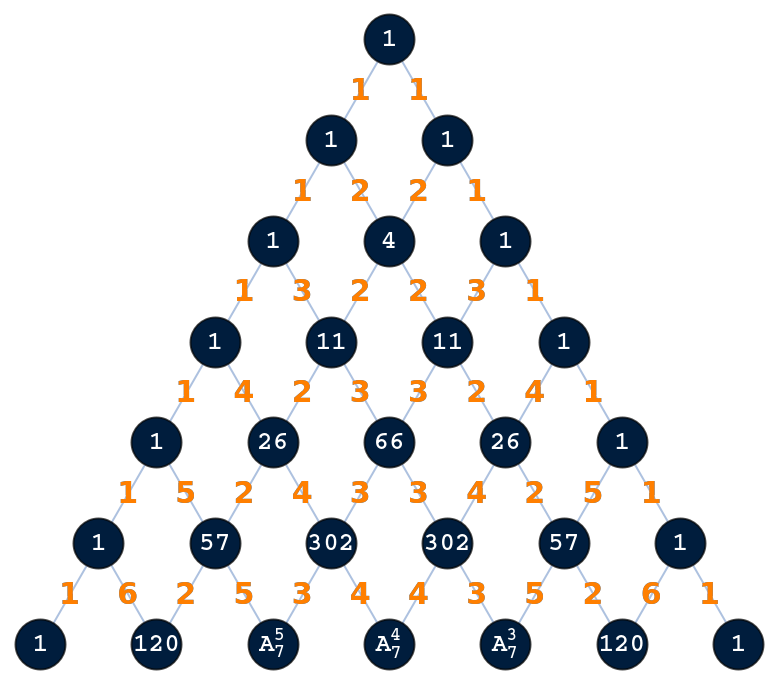

The sum of all elements in the n th row is Factorial[n], for example the 6th row:

In[6]:=
{6!, 1 + 57 + 302 + 302 + 57 + 1}
Out[6]=

Or the 7th row:

In[7]:=
{7!, 1 + 120 + 1191 + 2416 + 1191 + 120 + 1}
Out[7]=

Retrieve all numerical values from the graph nodes:

In[8]:=
n = 12; g = ResourceFunction["EulerianNumberTriangle"][n]; With[{vtx = ResourceFunction["EulerianNumber"] @@@ VertexList[g]}, Take[vtx, Binomial[#, 2] + {1, #}] & /@ Range[n]] // Column
Out[9]=

Possible Issues (1) 

Maximum visualization depth is 41 layers with n=40. For larger value the function returns unevaluated:

In[10]:=
ResourceFunction["EulerianNumberTriangle"][100]
Out[10]=

Neat Examples (2) 

The ArrayPlot of the adjacency matrix for an Eulerian number triangle:

In[11]:=
g = ResourceFunction["EulerianNumberTriangle"][10];
In[12]:=
(wm = WeightedAdjacencyMatrix[g]) // ArrayPlot
Out[12]=

All eigenvalues are real because of the matrix itself is real and symmetric:

In[13]:=
Eigenvalues[wm // N] // Chop
Out[13]=

Publisher

Shenghui Yang

Version History

  • 1.0.0 – 06 August 2025

Source Metadata

Related Resources

License Information