Basic Examples (6)
Define a Stratonovich process:
Square transformation of the process:
Start with a Stratonovich process:
Cubic transformation of a process:
Start with a geometric Brownian motion process:
Log transformation of the process:
Show the PDF of the transformed process:
Start with an Ornstein-Uhlenbeck process:
Log transformation of the process:
Define the following Stratonovich process:
Perform a reciprocal transformation:
Start with a 2D process:
Two variable linear transformation of the process:
Scope (4)
Start with an OrnsteinUhlenbeck process:
Consider the transformation y = ⅇθ t(x-μ) that is time dependent:
Check the process is drift-less for this transformation:
Define a 2D Stratonovich process:
Transform coordinates to polar:
Start with a general process with drift a and diffusion b:
Time dependent scaling:
Define a process in cylindrical coordinates:
Perform a transformation to spherical coordinates using long names notation:
Options (3)
Assumptions (3)
Start with a Stratonovich process:
Tangent/Cauchy transformation of Stratonovich process:
Specify a solving branch for 0<=x<2π:
Stratonovich process generated from a CoxIngersollRoss process:
Square root(Lamperti) transformation:
Define the following process:
Transform the process, pass the transformation in implicit form x = Log(y/1-y):
Applications (15)
2D stochastic trapping central force (5)
Define a stochastic process representing harmonic oscillator trap(including a magnetic effect) in Cartesian coordinates:
Change to polar coordinates that are more suitable to the problem:
Set up parameters and simulate 5 paths:
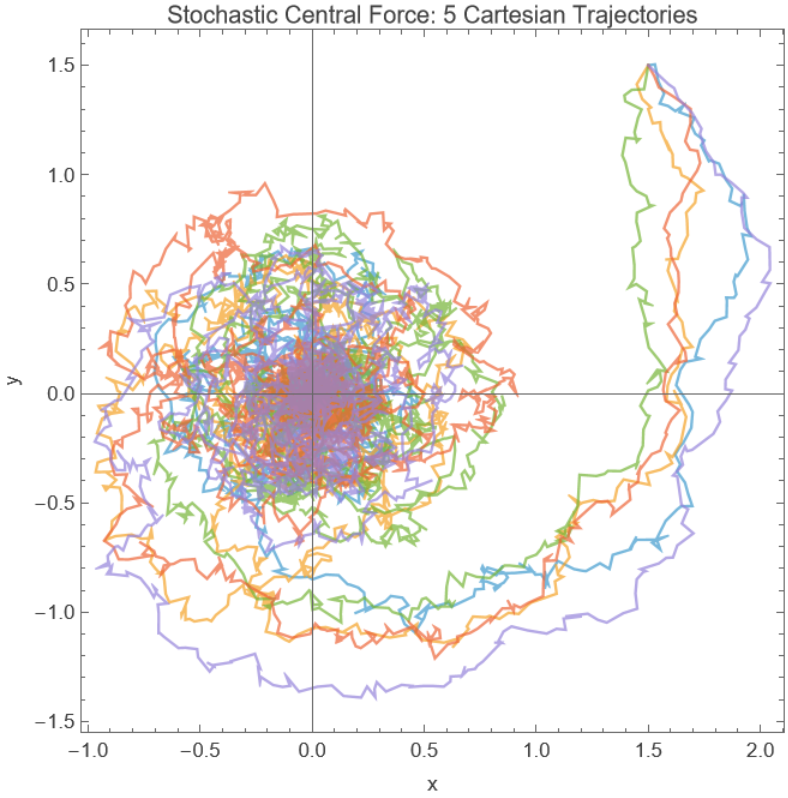
Swap back to Cartesian coordinates for plotting:
Plot the paths:
Gompertz stochastic growth (4)
Define a stochastic process representing the Gompertz growth equation with noise:
Logarithmic variable change:
The process becomes OrnsteinUhlenbeck after the transformation with parameters:
Check the PDF are the same:
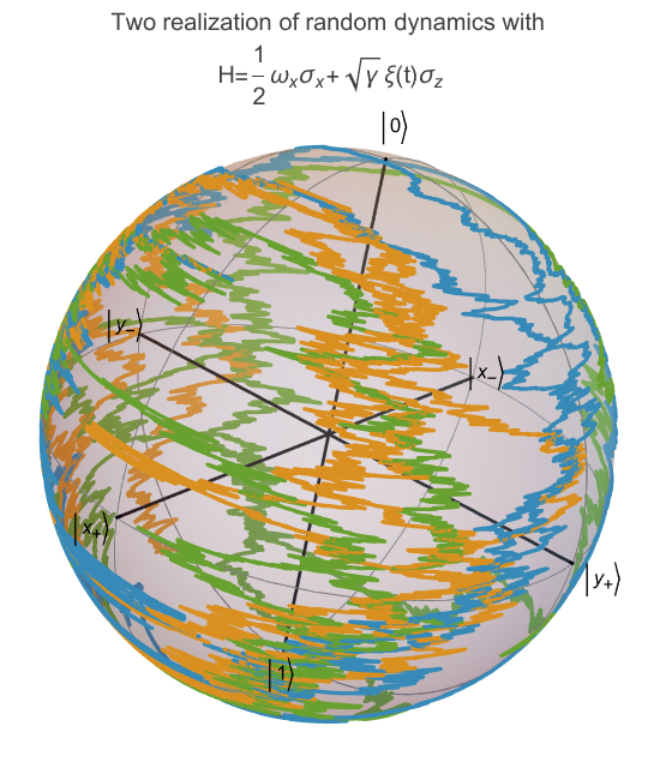
Stochastic Schrodinger equation (6)
Define the terms with ⅆt and ∘ⅆWt of the stochastic differential equation in Cartesian coordinates, the terms originate from the following equation
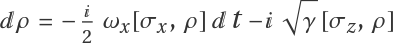 ∘ⅆWt for some density matrix ρ expressed as a Bloch vector:
∘ⅆWt for some density matrix ρ expressed as a Bloch vector:
Build the Stratonovich process:
Transform to spherical coordinates:
Generate 100 realizations for the density matrix:
Switch back to Cartesian coordinates for plotting:
Show the Bloch vector trajectories on the Bloch sphere for three realizations:

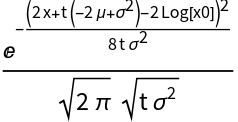

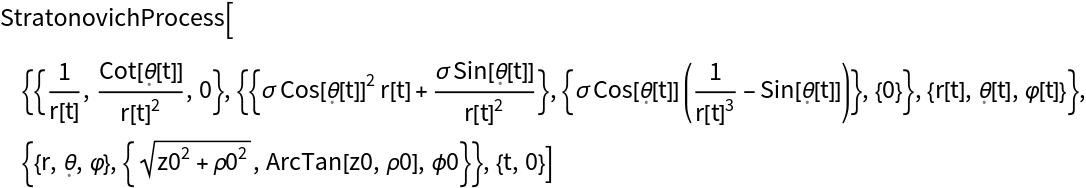
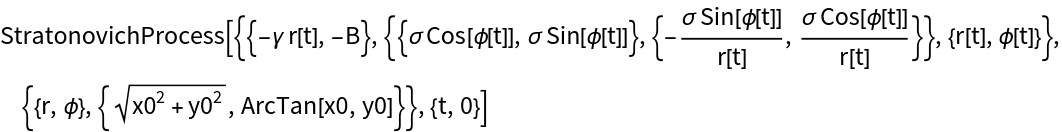
![]() ∘ⅆWt for some density matrix ρ expressed as a Bloch vector:
∘ⅆWt for some density matrix ρ expressed as a Bloch vector:![SDEnonRandom = {0, -z \[Omega]x, y \[Omega]x};
SDErandom = {-2 y Sqrt[\[Gamma]], 2 x Sqrt[\[Gamma]], 0};](https://www.wolframcloud.com/obj/resourcesystem/images/8e8/8e8e0160-7b07-4a7a-b988-316c2e257753/473ec4eaed2923c7.png)
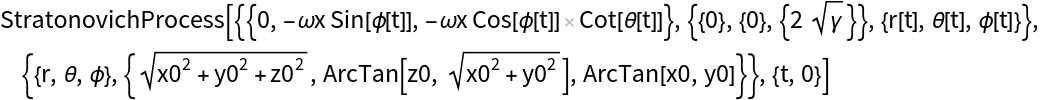
![cartesianBlochPaths = TimeSeriesMap[{#[[1]] Sin[#[[2]]] Cos[#[[3]]], #[[
1]] Sin[#[[2]]] Sin[#[[3]]], #[[1]] Cos[#[[2]]]} &, paths];](https://www.wolframcloud.com/obj/resourcesystem/images/8e8/8e8e0160-7b07-4a7a-b988-316c2e257753/26b2e9f13b51ac25.png)