Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Convert an explicit list of rules into an enumerated Turing machine specification
ResourceFunction["TuringMachineToNumber"][rules] converts rules to an enumerated Turing machine specification containing the rule number, number of states and number of colors. |
| si | initial state of the head |
| ai | initial value of the cell under the head |
| sf | final state of the head |
| af | final value of the cell under the head |
| offset | offset by which the head moves |
| n | number encoding the given rules |
| s | number of states in the Turing machine |
| k | number of tape cell colors in the Turing machine |
| 2-state, 2-color machines | 4096 |
| s-state, k-color machines | (2sk)^(sk) |
Convert a list of Turing machine rules into an enumerated specification:
| In[1]:= |
|
| Out[1]= |
|
Show that the two specifications are equivalent:
| In[2]:= |
|
| Out[2]= |
|
Generate all possible rules for a 1-state, 2-color Turing machine, ordered by rule number:
| In[3]:= |
|
| Out[3]= |
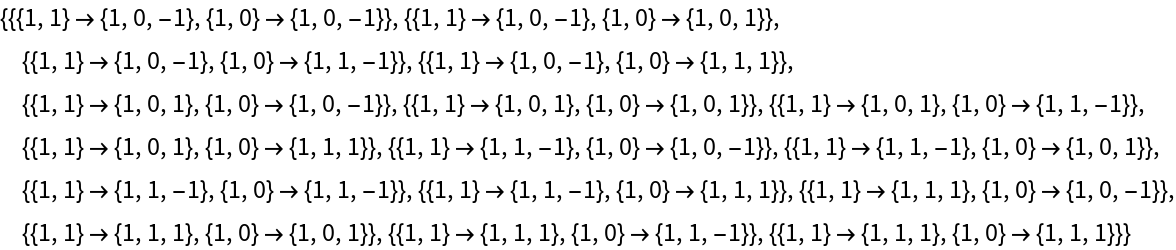
|
Convert the set of possible s = 1, k = 2 rules back to enumerated form:
| In[4]:= |
|
| Out[4]= |
|
In a valid Turing machine specification, head states must be integers greater than 0:
| In[5]:= |
|
| Out[5]= |
|
In a valid Turing machine specification, tape colors must be integers greater than or equal to 0:
| In[6]:= |
|
| Out[6]= |
|
TuringMachineToNumber cannot accept offsets with the head List:
| In[7]:= |
|
| Out[7]= |
|
TuringMachineToNumber cannot accept offsets that are not 1 or -1:
| In[8]:= |
|
| Out[8]= |
|
Turing machines that have multiple transformations for a single input configuration cannot be enumerated:
| In[9]:= |
|
| Out[9]= |
|
Turing machines that do not have a transformation for every possible input configuration cannot be enumerated:
| In[10]:= |
|
| Out[10]= |
|
This work is licensed under a Creative Commons Attribution 4.0 International License