Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Generate a tiling pattern from a set of Wang tiles
ResourceFunction["GenerateWangTiling"][tiles,{},n] covers an n× n array with edge-matching Wang tiles. | |
ResourceFunction["GenerateWangTiling"][tiles,{},{m,n}] covers an m× n array instead. | |
ResourceFunction["GenerateWangTiling"][tiles,{},size,All] lists all array coverings consistent with edge matching rules of the tiles. | |
ResourceFunction["GenerateWangTiling"][tiles,{},size,count] lists multiple coverings, up to integer count of them. | |
ResourceFunction["GenerateWangTiling"][tiles,seed,size,count] forces the seed tile to occur near the center of the pattern. |
Generate part of a Wang tiling from a set of just one tile:
| In[1]:= |
| Out[1]= |
Depict the 3×3 tiling as a Graphics object:
| In[2]:= | ![With[{wangGraphics = Function[{or, tile, colRules},
MapThread[{#,
EdgeForm[Black],
Polygon[
Append[
Map[or + #& , #2], or]]}& , {
ReplaceAll[
tile, colRules], {{{(-1)/2, (-1)/2}, {1/2, (-1)/2}}, {{1/2, (-1)/2}, {1/2, 1/2}}, {{1/2, 1/2}, {(-1)/2, 1/2}}, {{(-1)/2, 1/2}, {(-1)/2, (-1)/2}}}}, 1]]},
Show[#, ImageSize -> 150] &@MapIndexed[
Graphics@wangGraphics[
Reverse[#2 {-1, 1}], #1,
{0 -> Lighter[Red], 1 -> Lighter[Gray]}] &,
#, {2}] &@ResourceFunction["GenerateWangTiling"][
{{0, 1, 0, 1}}, {}, 3]]](https://www.wolframcloud.com/obj/resourcesystem/images/8e5/8e5a66eb-4fb3-4756-94c1-90d45daa5912/77b0ecb6897f6ef8.png) |
| Out[2]= |  |
Change the region size to 2×4:
| In[3]:= | ![With[{wangGraphics = Function[{or, tile, colRules},
MapThread[{#,
EdgeForm[Black],
Polygon[
Append[
Map[or + #& , #2], or]]}& , {
ReplaceAll[
tile, colRules], {{{(-1)/2, (-1)/2}, {1/2, (-1)/2}}, {{1/2, (-1)/2}, {1/2, 1/2}}, {{1/2, 1/2}, {(-1)/2, 1/2}}, {{(-1)/2, 1/2}, {(-1)/2, (-1)/2}}}}, 1]]},
Show[#, ImageSize -> 200] &@MapIndexed[
Graphics@wangGraphics[
Reverse[#2 {-1, 1}], #1,
{0 -> Lighter[Red], 1 -> Lighter[Gray]}] &,
#, {2}] &@ResourceFunction["GenerateWangTiling"][
{{0, 1, 0, 1}}, {}, {2, 4}]]](https://www.wolframcloud.com/obj/resourcesystem/images/8e5/8e5a66eb-4fb3-4756-94c1-90d45daa5912/677992f011caa45b.png) |
| Out[3]= | 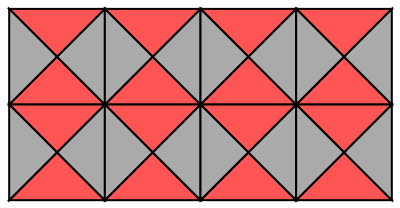 |
Plot a periodic pattern by alternating between two Wang tiles:
| In[4]:= | ![With[{wangGraphics = Function[{or, tile, colRules},
MapThread[{#,
EdgeForm[Black],
Polygon[
Append[
Map[or + #& , #2], or]]}& , {
ReplaceAll[
tile, colRules], {{{(-1)/2, (-1)/2}, {1/2, (-1)/2}}, {{1/2, (-1)/2}, {1/2, 1/2}}, {{1/2, 1/2}, {(-1)/2, 1/2}}, {{(-1)/2, 1/2}, {(-1)/2, (-1)/2}}}}, 1]], cols = {1 -> RGBColor[1, 0.75, 0], 2 -> RGBColor[0., 1., 0.5], 3 -> RGBColor[0.5, 0.5, 1.], 4 -> RGBColor[1., 0.4, 0.85]}},
Show[#, ImageSize -> 200] &@MapIndexed[
Graphics@wangGraphics[
Reverse[#2 {-1, 1}], #1, cols] &,
#, {2}] &@ResourceFunction["GenerateWangTiling"][
{{1, 3, 2, 4}, {2, 4, 1, 3}}, {1, 3, 2, 4}, 4]]](https://www.wolframcloud.com/obj/resourcesystem/images/8e5/8e5a66eb-4fb3-4756-94c1-90d45daa5912/30ed36d42c429431.png) |
| Out[4]= | 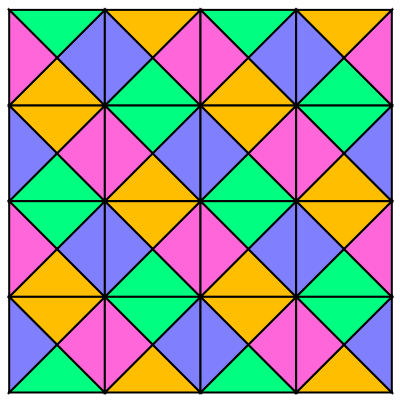 |
Shift the pattern's offset by changing the seed tile:
| In[5]:= | ![With[{wangGraphics = Function[{or, tile, colRules},
MapThread[{#,
EdgeForm[Black],
Polygon[
Append[
Map[or + #& , #2], or]]}& , {
ReplaceAll[
tile, colRules], {{{(-1)/2, (-1)/2}, {1/2, (-1)/2}}, {{1/2, (-1)/2}, {1/2, 1/2}}, {{1/2, 1/2}, {(-1)/2, 1/2}}, {{(-1)/2, 1/2}, {(-1)/2, (-1)/2}}}}, 1]], cols = {1 -> RGBColor[1, 0.75, 0], 2 -> RGBColor[0., 1., 0.5], 3 -> RGBColor[0.5, 0.5, 1.], 4 -> RGBColor[1., 0.4, 0.85]}},
Show[#, ImageSize -> 200] &@MapIndexed[
Graphics@wangGraphics[
Reverse[#2 {-1, 1}], #1, cols] &,
#, {2}] &@ResourceFunction["GenerateWangTiling"][
{{1, 3, 2, 4}, {2, 4, 1, 3}}, {2, 4, 1, 3}, 4]]](https://www.wolframcloud.com/obj/resourcesystem/images/8e5/8e5a66eb-4fb3-4756-94c1-90d45daa5912/0320a3eb12db18e1.png) |
| Out[5]= | 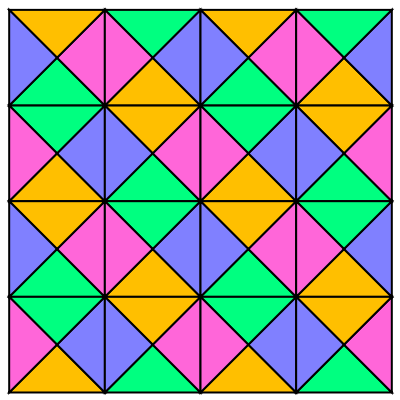 |
Verify that this tiling pattern in four colors has only two translates:
| In[6]:= |
| Out[6]= |
GenerateWangTiling can get returns for bigger tile sets with more colors:
| In[7]:= | ![With[{cols = MapIndexed[# -> Lighter[Hue[#2[[1]]/18], .5] &,
Flatten[Transpose[Partition[Range[16], 2]]]],
wangGraphics = Function[{or, tile, colRules},
MapThread[{#,
EdgeForm[Black],
Polygon[
Append[
Map[or + #& , #2], or]]}& , {
ReplaceAll[
tile, colRules], {{{(-1)/2, (-1)/2}, {1/2, (-1)/2}}, {{1/2, (-1)/2}, {1/2, 1/2}}, {{1/2, 1/2}, {(-1)/2, 1/2}}, {{(-1)/2, 1/2}, {(-1)/2, (-1)/2}}}}, 1]],
penroseTiles = {{1, 5, 3, 1}, {7, 2, 3, 1}, {1, 5, 12, 9}, {7, 2, 12, 9}, {1, 7, 12, 11}, {1, 4, 10, 16}, {1, 14, 6, 11}, {7, 10, 6, 9}, {2, 2, 4, 6}, {8, 2, 4, 1}, {2, 10, 11, 6}, {8, 10, 11, 1}, {2,
12, 11, 8}, {2, 15, 9, 3}, {2, 12, 5, 13}, {8, 10, 5, 9}, {4, 3, 2, 7}, {4, 3, 8, 4}, {10, 11, 2, 7}, {10, 11, 8, 4}, {10, 9, 2, 5}, {12, 13, 2, 2}, {5, 9, 2, 15}, {5, 11, 8, 12}, {3, 8, 1, 4}, {
3, 3, 7, 4}, {9, 8, 1, 12}, {9, 3, 7, 12}, {9, 6, 1, 10}, {11, 1, 1, 14}, {6, 16, 1, 10}, {6, 11, 7, 12}}},
Labeled[Show[#, ImageSize -> 600] &@MapIndexed[
Graphics@wangGraphics[
Reverse[#2 {-1, 1}], #1, cols] &,
#, {2}] &@ResourceFunction["GenerateWangTiling"][
penroseTiles, {}, 20],
Grid[Partition[Graphics[wangGraphics[{0, 0}, #, cols],
ImageSize -> 30] & /@ penroseTiles, 16]]]]](https://www.wolframcloud.com/obj/resourcesystem/images/8e5/8e5a66eb-4fb3-4756-94c1-90d45daa5912/4f08328a1a6db2ad.png) |
| Out[7]= |  |
GenerateWangTiling can also check boundary conditions:
| In[8]:= | ![ResourceFunction["GenerateWangTiling"][
{{1, 3, 2, 4}, {2, 4, 1, 3}}, {}, #, All,
"Boundary" -> "Periodic"] /. {
x_List :> Length[x]} & /@ Range[3, 6]](https://www.wolframcloud.com/obj/resourcesystem/images/8e5/8e5a66eb-4fb3-4756-94c1-90d45daa5912/7bd292d80e18eb8d.png) |
| Out[8]= |
Plot a section of the minimal-known aperiodic Wang tiling:
| In[9]:= | ![With[{JeandelRaoTiles = {{1, 0, 0, 0}, {1, 2, 0, 2}, {2, 3, 1, 0}, {1,
0, 1, 3}, {1, 1, 1, 3}, {3, 3, 1, 3}, {2, 0, 2, 1}, {0, 1, 2, 1}, {0, 2, 2, 2}, {2, 1, 2, 3}, {2, 3, 3, 1}}, cols = {1 -> RGBColor[1., 0.4, 0.85], 2 -> RGBColor[0.5, 0.5, 1.], 3 -> RGBColor[1, 0.75, 0], 0 -> GrayLevel[0.85]},
wangGraphics = Function[{or, tile, colRules},
MapThread[{#,
EdgeForm[Black],
Polygon[
Append[
Map[or + #& , #2], or]]}& , {
ReplaceAll[
tile, colRules], {{{(-1)/2, (-1)/2}, {1/2, (-1)/2}}, {{1/2, (-1)/2}, {1/2, 1/2}}, {{1/2, 1/2}, {(-1)/2, 1/2}}, {{(-1)/2, 1/2}, {(-1)/2, (-1)/2}}}}, 1]]},
Labeled[Show[#, ImageSize -> 600] &@MapIndexed[
Graphics@wangGraphics[
Reverse[#2 {-1, 1}], #1, cols] &,
#, {2}] &@ResourceFunction["GenerateWangTiling"][
JeandelRaoTiles, {}, 20],
Row[Graphics[wangGraphics[{0, 0}, #, cols],
ImageSize -> 30] & /@ JeandelRaoTiles,
Spacer[3]]]]](https://www.wolframcloud.com/obj/resourcesystem/images/8e5/8e5a66eb-4fb3-4756-94c1-90d45daa5912/5754688f661d39f0.png) |
| Out[9]= |  |
This work is licensed under a Creative Commons Attribution 4.0 International License