Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Enumerate the graph minors of a graph
ResourceFunction["GraphMinors"][g] gives a list of the graph minors of the graph g. |
Find the minors of a simple graph:
| In[1]:= | ![ResourceFunction["GraphMinors"][\!\(\*
GraphicsBox[
NamespaceBox["NetworkGraphics",
DynamicModuleBox[{Typeset`graph = HoldComplete[
Graph[{1, 2, 3, 4}, {Null,
SparseArray[
Automatic, {4, 4}, 0, {1, {{0, 3, 6, 9, 12}, {{2}, {3}, {4}, {1}, {3}, {4}, {
1}, {2}, {4}, {1}, {2}, {3}}}, Pattern}]}]]},
TagBox[GraphicsGroupBox[
GraphicsComplexBox[{{-1., 1.0106430996148606`*^-15}, {-7.044813998280222*^-16, 1.}, {
1., -1.133107779529596*^-15}, {
6.049014748177263*^-16, -1.}}, {
{Hue[0.6, 0.7, 0.5], Opacity[0.7], LineBox[{{1, 2}, {1, 3}, {1, 4}, {2, 3}, {2, 4}, {3, 4}}]},
{Hue[0.6, 0.2, 0.8], EdgeForm[{GrayLevel[0], Opacity[0.7]}], DiskBox[1, 0.02261146496815286], DiskBox[2, 0.02261146496815286], DiskBox[3, 0.02261146496815286], DiskBox[4, 0.02261146496815286]}}]],
MouseAppearanceTag["NetworkGraphics"]],
AllowKernelInitialization->False]],
DefaultBaseStyle->{"NetworkGraphics", FrontEnd`GraphicsHighlightColor -> Hue[0.8, 1., 0.6]},
FormatType->TraditionalForm,
FrameTicks->None]\)]](https://www.wolframcloud.com/obj/resourcesystem/images/8d4/8d409cc8-c703-4e73-a5d1-8f15d96ba50d/40fa9b544a186a17.png) |
| Out[1]= | 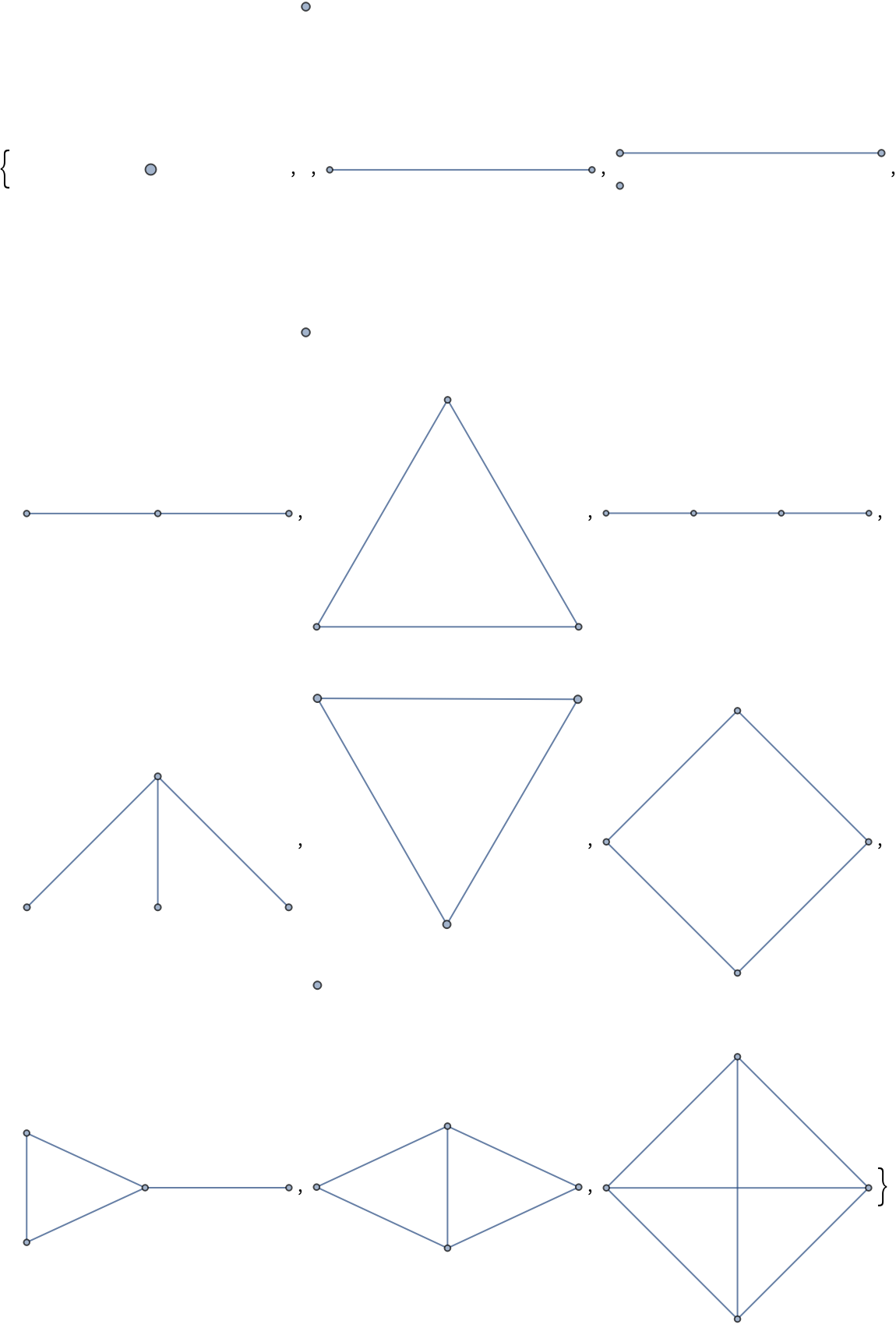 |
Minors of the octahedral graph:
| In[2]:= | ![ResourceFunction["GraphMinors"][\!\(\*
Graphics3DBox[
NamespaceBox["NetworkGraphics",
DynamicModuleBox[{Typeset`graph = HoldComplete[
Graph[{1, 2, 3, 4, 5, 6}, {Null, {{1, 2}, {2, 3}, {3, 1}, {1, 4}, {1, 5}, {2, 5}, {
2, 6}, {3, 6}, {3, 4}, {4, 5}, {5, 6}, {6, 4}}}, {GraphLayout -> {"Dimension" -> 3}}]]},
TagBox[GraphicsGroup3DBox[
GraphicsComplex3DBox[{{0.31998376993941036`, 0., 0.28523505366058577`}, {0.791662602205063, 0.19781286610305127`, 1.1447447319948134`}, {0., 0.7446635845653324, 0.8710709882885987}, {0.4437799056271618,
0.9507644413111068, 0.}, {1.2360713368032015`, 0.40416526345661496`, 0.27272421192218343`}, {
0.9150718278337522, 1.1474240714174644`, 0.8588688745086416}}, {
{Hue[0.6, 0.2, 0.8],
{Arrowheads[0.], Arrow3DBox[TubeBox[{{{0.31998376993941036`, 0., 0.28523505366058577`}, {0.791662602205063, 0.19781286610305127`, 1.1447447319948134`}}}], 0.03219195933111224]},
{Arrowheads[0.], Arrow3DBox[TubeBox[{{{0.31998376993941036`, 0., 0.28523505366058577`}, {0., 0.7446635845653324, 0.8710709882885987}}}], 0.03219195933111224]},
{Arrowheads[0.], Arrow3DBox[TubeBox[{{{0.31998376993941036`, 0., 0.28523505366058577`}, {0.4437799056271618, 0.9507644413111068, 0.}}}], 0.03219195933111224]},
{Arrowheads[0.], Arrow3DBox[TubeBox[{{{0.31998376993941036`, 0., 0.28523505366058577`}, {1.2360713368032015`, 0.40416526345661496`, 0.27272421192218343`}}}], 0.03219195933111224]},
{Arrowheads[0.], Arrow3DBox[TubeBox[{{{0.791662602205063, 0.19781286610305127`, 1.1447447319948134`}, {0., 0.7446635845653324, 0.8710709882885987}}}], 0.03219195933111224]},
{Arrowheads[0.], Arrow3DBox[TubeBox[{{{0.791662602205063, 0.19781286610305127`, 1.1447447319948134`}, {
1.2360713368032015`, 0.40416526345661496`, 0.27272421192218343`}}}], 0.03219195933111224]},
{Arrowheads[0.], Arrow3DBox[TubeBox[{{{0.791662602205063, 0.19781286610305127`, 1.1447447319948134`}, {
0.9150718278337522, 1.1474240714174644`, 0.8588688745086416}}}], 0.03219195933111224]},
{Arrowheads[0.], Arrow3DBox[TubeBox[{{{0., 0.7446635845653324, 0.8710709882885987}, {0.4437799056271618, 0.9507644413111068, 0.}}}], 0.03219195933111224]},
{Arrowheads[0.], Arrow3DBox[TubeBox[{{{0., 0.7446635845653324, 0.8710709882885987}, {0.9150718278337522, 1.1474240714174644`, 0.8588688745086416}}}], 0.03219195933111224]},
{Arrowheads[0.], Arrow3DBox[TubeBox[{{{0.4437799056271618, 0.9507644413111068, 0.}, {1.2360713368032015`, 0.40416526345661496`, 0.27272421192218343`}}}], 0.03219195933111224]},
{Arrowheads[0.], Arrow3DBox[TubeBox[{{{0.4437799056271618, 0.9507644413111068, 0.}, {0.9150718278337522, 1.1474240714174644`, 0.8588688745086416}}}], 0.03219195933111224]},
{Arrowheads[0.], Arrow3DBox[TubeBox[{{{1.2360713368032015`, 0.40416526345661496`, 0.27272421192218343`}, {
0.9150718278337522, 1.1474240714174644`, 0.8588688745086416}}}], 0.03219195933111224]}},
{Hue[0.6, 0.6, 1], SphereBox[1, 0.03219195933111224], SphereBox[2, 0.03219195933111224], SphereBox[3, 0.03219195933111224], SphereBox[4, 0.03219195933111224], SphereBox[5, 0.03219195933111224], SphereBox[6, 0.03219195933111224]}}]],
MouseAppearanceTag["NetworkGraphics"]],
AllowKernelInitialization->False]],
Boxed->False,
DefaultBaseStyle->{"NetworkGraphics", FrontEnd`GraphicsHighlightColor -> Hue[0.8, 1., 0.6]},
FormatType->TraditionalForm,
Lighting->{{"Directional",
GrayLevel[0.7],
ImageScaled[{1, 1, 0}]}, {"Point",
GrayLevel[0.9],
ImageScaled[{0, 0, 0}], {0, 0, 0.07}}}]\)]](https://www.wolframcloud.com/obj/resourcesystem/images/8d4/8d409cc8-c703-4e73-a5d1-8f15d96ba50d/1dc69d2d07050400.png) |
| Out[2]= | 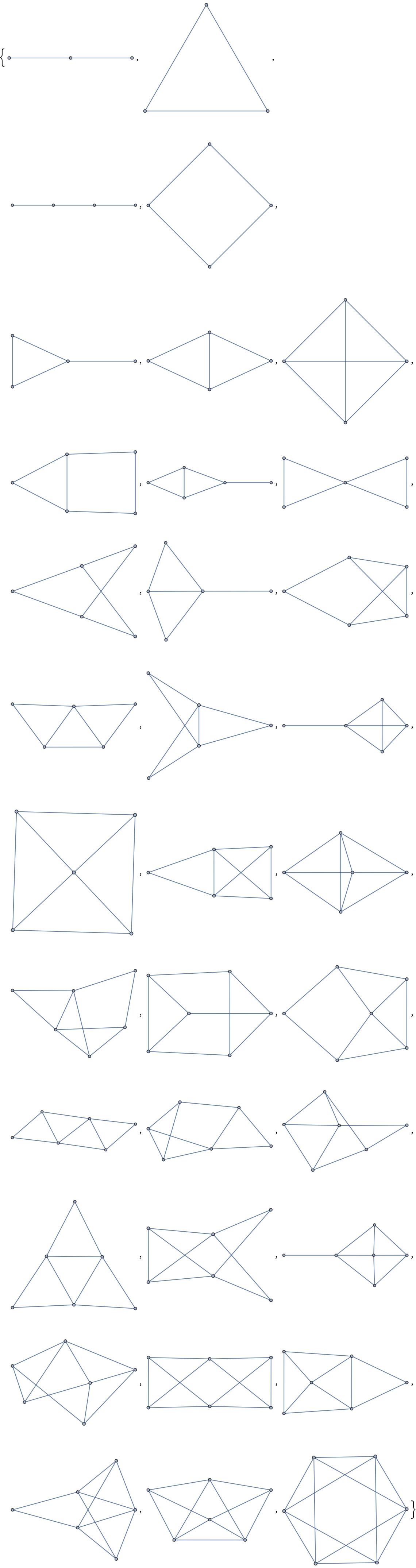 |
Demonstrate the Kuratowski reduction theorem on the 16-cell graph:
| In[3]:= |
| Out[3]= | 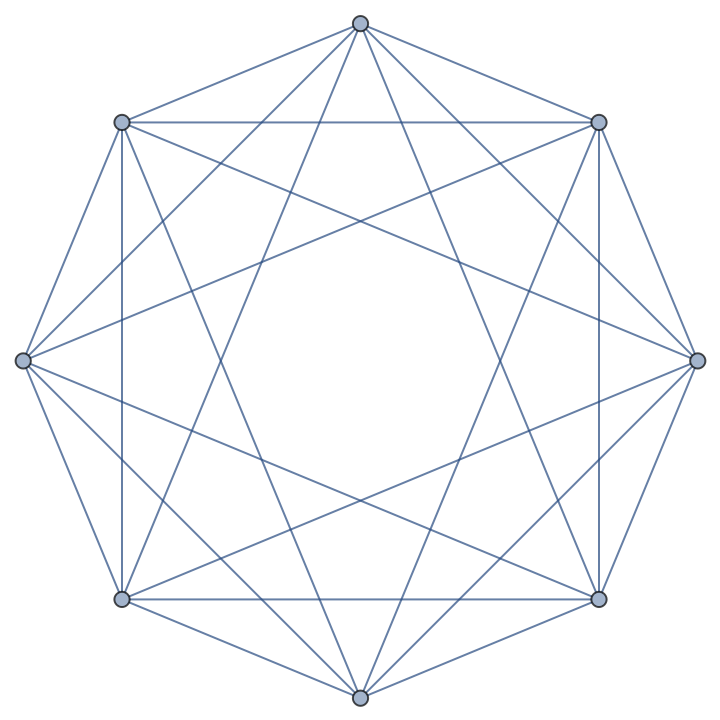 |
| In[4]:= |
| Out[4]= |
The pentatope graph is one of the graph minors:
| In[5]:= | ![MemberQ[ResourceFunction["GraphMinors"][hg], g_?GraphQ /; IsomorphicGraphQ[g, GraphData["PentatopeGraph"]]]](https://www.wolframcloud.com/obj/resourcesystem/images/8d4/8d409cc8-c703-4e73-a5d1-8f15d96ba50d/44586ab5938f2aab.png) |
| Out[5]= |
This work is licensed under a Creative Commons Attribution 4.0 International License