Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Conduct an empirically derived test that assesses randomness using the frequencies of serial combinations of 0s and 1s
ResourceFunction["SerialRandomnessTest"][sequence] conducts an empirically derived test using the frequencies of serial combinations of 0s and 1s in sequence and returns an associated p-value. | |
ResourceFunction["SerialRandomnessTest"][sequence,"properties"] conducts an empirically derived test and returns the specified property. |
| "TestStatistic" | returns the test statistic |
| "PValue" | returns the p-value associated with the test |
Generate a sequence of random integers:
| In[1]:= |
Visualize the sequence:
| In[2]:= |
| Out[2]= |  |
Apply a runs-based test:
| In[3]:= |
| Out[3]= |
| In[4]:= |
| Out[4]= |
Generate a sequence of random integers:
| In[5]:= |
| In[6]:= |
Visualize the sequence:
| In[7]:= |
| Out[7]= |  |
Attempt to reject a non-random sequence:
| In[8]:= |
| Out[8]= |
| In[9]:= |
| Out[9]= |
Test the randomness of rule 30:
| In[10]:= |
| In[11]:= |
| Out[11]= |  |
| In[12]:= |
| Out[12]= |
SerialRandomnessTest requires sequences of length 100 or more:
| In[13]:= |
Visualize the sampling distribution of the test statistic:
| In[14]:= |
| In[15]:= |
| Out[15]= | 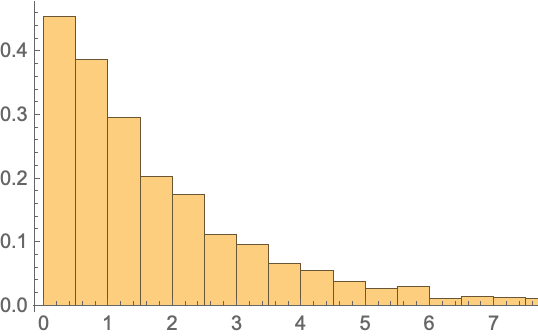 |
| In[16]:= |
| Out[16]= |
| In[17]:= |
| Out[17]= | 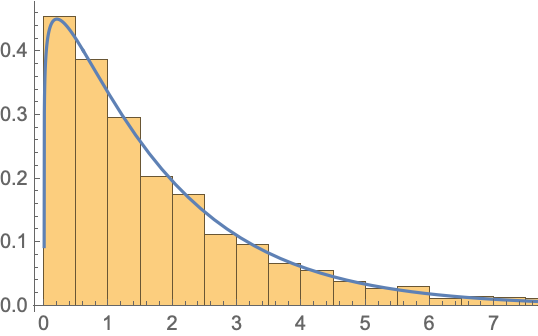 |
This work is licensed under a Creative Commons Attribution 4.0 International License