Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Find finite models consistent with the set of relations
ResourceFunction["FindFiniteModels"][rels] finds models in form of multiplication tables consistent with the relations rels for each operator in rels, assuming each variable can have one of two values. | |
ResourceFunction["FindFiniteModels"][rels,k] allows k≥2 values for each variable. | |
ResourceFunction["FindFiniteModels"][rels,k,prop] returns a specified property prop of found models. |
| "Association" | returns an association with multiplication tables as values and indices as keys for each found model (default) |
| "Indices" | returns a list of indices for models |
| "Models" | returns a list of models |
| Method | "ExpressionPrune" | the method to use |
| "Parallelize" | False | whether to run some operations in parallel |
| MaxItems | Infinity | limit the number of returned models |
| "ReverseOrdering" | False | ordering of indices |
| "ExpressionPrune" | pruned search over relations converted to a conjunction of DNFs |
| "BruteForce" | a complete search over all possible models |
| Automatic | same as "ExpressionPrune" |
Find binary models for a nullary operator:
| In[1]:= |
| Out[1]= |
Find ternary models for a nullary operator:
| In[2]:= |
| Out[2]= |
Find binary models for unary operators:
| In[3]:= |
| Out[3]= |
| In[4]:= |
| Out[4]= |
| In[5]:= |
| Out[5]= |
Find binary models for a binary operator:
| In[6]:= |
| Out[6]= |
Find ternary models for a binary operator:
| In[7]:= |
| Out[7]= |  |
Find binary models for a ternary operator:
| In[8]:= |
| Out[8]= | 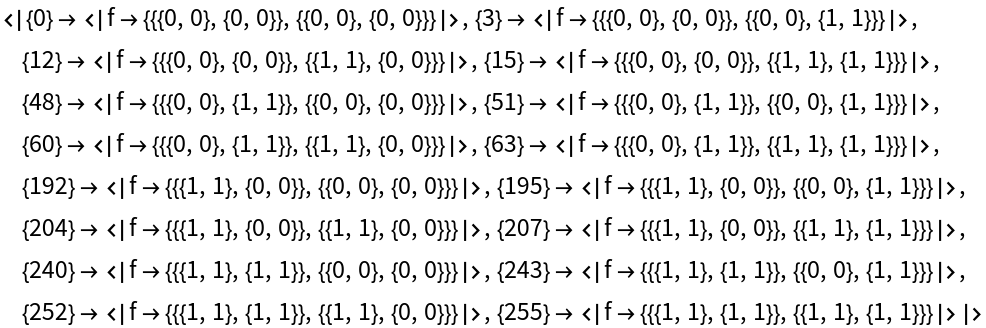 |
Include constants:
| In[9]:= |
| Out[9]= |
In absence of operators, FindFiniteModels assumes all atoms are nullary operators:
| In[10]:= |
| Out[10]= |
Multiple operators with different arities is supported:
| In[11]:= |
| Out[11]= |  |
Inequalities:
| In[12]:= |
| Out[12]= |
| In[13]:= |
| Out[13]= |
| In[14]:= |
| Out[14]= |
Alternatives:
| In[15]:= |
| Out[15]= |
Disjunctions:
| In[16]:= |
| Out[16]= | 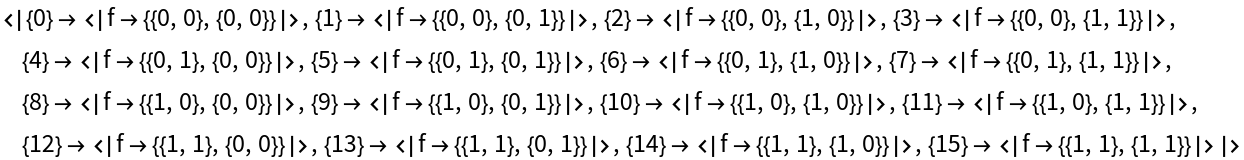 |
Quantifiers:
| In[17]:= |
| Out[17]= | 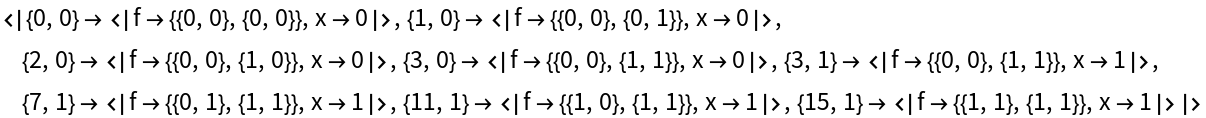 |
| In[18]:= |
| Out[18]= |
String relations have additional axioms:
| In[19]:= |
| Out[19]= |
String relations form a monoid with binary associative operator ∘ (\[SmallCircle]) and nullary identity 1:
| In[20]:= | ![ResourceFunction["FindFiniteModels"]["A" -> "AA", 3] == ResourceFunction[
"FindFiniteModels"][{"A" == "A"\[SmallCircle]"A", ("A"\[SmallCircle]"B")\[SmallCircle]"C" == "A"\[SmallCircle]("B"\[SmallCircle]"C"), "1"[]\[SmallCircle]"A" == "A", "A"\[SmallCircle]"1"[] == "A"}, 3]](https://www.wolframcloud.com/obj/resourcesystem/images/8d1/8d12c305-1d22-4292-91fb-af2dc0450641/02bf422da1af1eab.png) |
| Out[20]= |
"BruteForce" method may be useful if a relation is very general so that enumerating models and finding a small subset of them returns faster:
| In[21]:= |
| Out[21]= |
| In[22]:= |
| Out[22]= |
Setting the option "Parallelize" to True may speed up computation:
| In[23]:= |
| Out[23]= |
| In[24]:= |
| Out[24]= |
| In[25]:= |
| Out[25]= |  |
| In[26]:= |
| Out[26]= |  |
Limiting a number of returned models reduces an amount of performed computation:
| In[27]:= |
| Out[27]= |  |
By default, models are indexed by their corresponding inputs (shifted by 1). For example, a model of Not for BooleanAxioms is {1, 0} because {1, 0}[[0+1]] ==1 and {1, 0}[[1+1]] ==0:
| In[28]:= |
| Out[28]= |
For some cases, like the default ordering of truth tables for boolean expressions, the convention is to use a reversed ordering {1,0}<->{True,False}:
| In[29]:= |
| Out[29]= |
For the first {8, 14, 1}, with "ReverseOrdering"→True, model indices correspond exactly to BooleanFunction indices and models to truth tables. Here CirclePlus is a model of And:
| In[30]:= |
| Out[30]= |
| In[31]:= |
| Out[31]= | 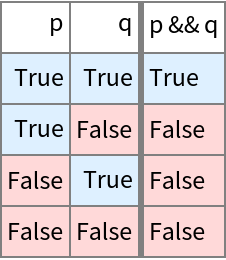 |
CircleTimes is a model of Or:
| In[32]:= |
| Out[32]= |
| In[33]:= |
| Out[33]= | 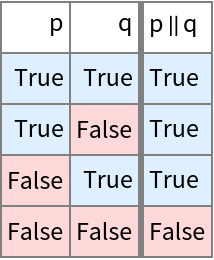 |
| In[34]:= |
| Out[34]= |
| In[35]:= |
| Out[35]= | 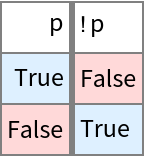 |
Define functions to be used throughout this example:
| In[36]:= | ![NestedTupleFromIndex[index_, k_, n_] := ArrayReshape[IntegerDigits[index, k, k^n], Table[k, n]]
plotRelationConstraints // ClearAll
plotRelationConstraints[expr_, k_ : 2, limit_ : Infinity, n_ : UpTo[6]] := Module[{indices = ResourceFunction["FindFiniteModels"][expr, k, "Indices", "Parallelize" -> True, MaxItems -> limit], sampleIndices, tables},
sampleIndices = Take[indices, n];
tables = Map[NestedTupleFromIndex[#[[1]], k, 2] &, sampleIndices];
Framed@Row[
Append[
ArrayPlot[#, Mesh -> True, ImageSize -> 32] & /@ tables, If[Length[sampleIndices] == 0, Row@{"(", 0, ")"}, If[Length[indices] - Length[sampleIndices] > 0, Row@{"\[Ellipsis]", "(", Length[indices], ")"}, Nothing]]
]
]
]](https://www.wolframcloud.com/obj/resourcesystem/images/8d1/8d12c305-1d22-4292-91fb-af2dc0450641/0257f1c15f791a86.png) |
Find models for abelian semigroup theory axioms:
| In[37]:= |
| Out[37]= |  |
Reproduce and extend some :
| In[38]:= | ![Scan[relation |-> Print[AbsoluteTiming@
Row[Riffle[
Prepend[plotRelationConstraints[{relation}, #] & /@ Range[2, 4],
Framed[relation, Background -> LightGray]], Spacer[8]]]], {b\[SmallCircle](a\[SmallCircle]a) == a, b\[SmallCircle](a\[SmallCircle]b) == a, b\[SmallCircle](b\[SmallCircle]a) == a}]](https://www.wolframcloud.com/obj/resourcesystem/images/8d1/8d12c305-1d22-4292-91fb-af2dc0450641/2086f90f8aac50fd.png) |

| In[39]:= | ![Scan[relation |-> Print[AbsoluteTiming@
Row[Riffle[
Prepend[plotRelationConstraints[{relation}, #] & /@ Range[2, 6],
Framed[relation, Background -> LightGray]], Spacer[8]]]], {b\[SmallCircle](a\[SmallCircle]a) == a, b\[SmallCircle](a\[SmallCircle]b) == a}]](https://www.wolframcloud.com/obj/resourcesystem/images/8d1/8d12c305-1d22-4292-91fb-af2dc0450641/3db1fcc7c56c5671.png) |


| In[40]:= | ![Scan[relation |-> Print[AbsoluteTiming@
Row[Riffle[
Prepend[plotRelationConstraints[{relation}, #, 2] & /@ Range[2, 10], Framed[relation, Background -> LightGray]], Spacer[8]]]], {b\[SmallCircle](a\[SmallCircle]a) == a, b\[SmallCircle](a\[SmallCircle]b) == a}]](https://www.wolframcloud.com/obj/resourcesystem/images/8d1/8d12c305-1d22-4292-91fb-af2dc0450641/7e669faa6c572b6a.png) |


| In[41]:= | ![Scan[relation |-> Print[AbsoluteTiming@
Row[Riffle[
Prepend[plotRelationConstraints[{relation}, #] & /@ Range[2, 3],
Framed[relation, Background -> LightGray]], Spacer[8]]]], {b\[SmallCircle](a\[SmallCircle]a) == 0}]](https://www.wolframcloud.com/obj/resourcesystem/images/8d1/8d12c305-1d22-4292-91fb-af2dc0450641/129cbe43cf7c8287.png) |
| In[42]:= | ![Scan[relation |-> Print[AbsoluteTiming@
Row[Riffle[
Prepend[plotRelationConstraints[{relation}, #] & /@ Range[2, 10], Framed[relation, Background -> LightGray]], Spacer[8]]]], {a\[SmallCircle]b == a, b\[SmallCircle]a == a}]](https://www.wolframcloud.com/obj/resourcesystem/images/8d1/8d12c305-1d22-4292-91fb-af2dc0450641/2d54a0b61fc306d8.png) |
Find models for the Wolfram axiom:
| In[43]:= |
| Out[43]= |
| In[44]:= |
| Out[44]= |
| In[45]:= |
| Out[45]= |  |
AxiomaticTheory examples:
| In[46]:= |
| Out[46]= |
| In[47]:= |
| Out[47]= |  |
| In[48]:= |
| Out[48]= |
| In[49]:= |
| Out[49]= |  |
| In[50]:= |
| Out[50]= |
| In[51]:= |
| Out[51]= |
| In[52]:= |
| Out[52]= |
This work is licensed under a Creative Commons Attribution 4.0 International License