Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
A sigmoidal interpolating rational function
ResourceFunction["RationalSmoothStep"][x] gives a rational sigmoidal function between [0,1] for a position x in [0,1]. | |
ResourceFunction["RationalSmoothStep"][n,x] is the rational smoothstep function of order n at position x. |
Interpolate at a position on a step:
| In[1]:= |
| Out[1]= |
Show rational smooth steps for multiple orders:
| In[2]:= | ![Plot[Evaluate[
Table[ResourceFunction["RationalSmoothStep"][n, x], {n, 2, 4}]], {x, -1/2, 3/2}, PlotLegends -> Range[2, 4]]](https://www.wolframcloud.com/obj/resourcesystem/images/8a2/8a2f16d3-753f-411e-b8fa-88e556b38ec0/643c0b29a27233af.png) |
| Out[2]= | 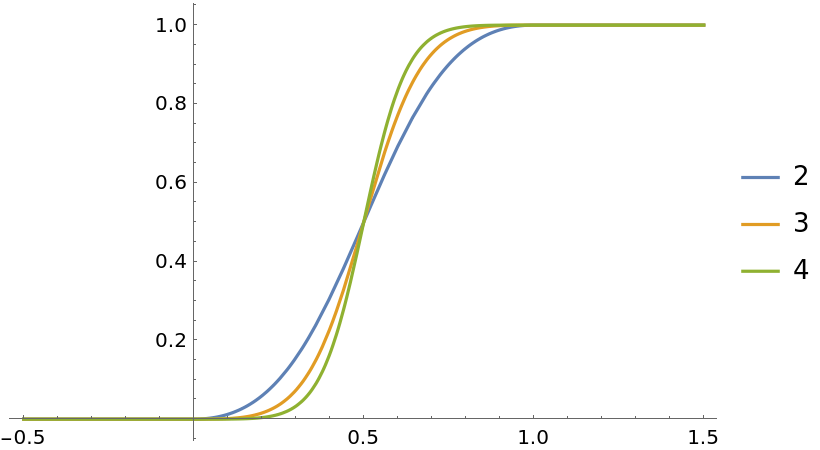 |
Evaluate at an exact position:
| In[3]:= |
| Out[3]= |
At a numeric position:
| In[4]:= |
| Out[4]= |
RationalSmoothStep threads over lists:
| In[5]:= |
| Out[5]= |
| In[6]:= |
| Out[6]= |
Use RationalSmoothStep to implement a "smooth" version of Hue (reference):
| In[7]:= | ![SmoothHue[n_Integer?NonNegative, h_?NumberQ, s_ : 1, b_ : 1] /; 0 <= s <= 1 && 0 <= b <= 1 := RGBColor[
b (1 - s + s ResourceFunction["RationalSmoothStep"][n, Clip[Abs[Mod[6 h + {0, 4, 2}, 6] - 3] - 1, {0, 1}]])]](https://www.wolframcloud.com/obj/resourcesystem/images/8a2/8a2f16d3-753f-411e-b8fa-88e556b38ec0/05c896d465170317.png) |
| In[8]:= |
| Out[8]= |
| In[9]:= |
| Out[9]= |  |
RationalSmoothStep satisfies a symmetry relation:
| In[10]:= |
| Out[10]= |
Use RationalSmoothStep to demonstrate "ease-in/ease-out":
| In[11]:= | ![Manipulate[
Graphics[
Text["Zoom!", {ResourceFunction["RationalSmoothStep"][n, x], 0}], PlotRange -> {{-.1, 1.1}, {-.1, .1}}], {{n, 2}, 1, 5, 1}, {x, -1, 2,
ControlType -> Animator, AnimationRunning -> False}]](https://www.wolframcloud.com/obj/resourcesystem/images/8a2/8a2f16d3-753f-411e-b8fa-88e556b38ec0/081ab3fa3c9b2b87.png) |
| Out[11]= |  |
This work is licensed under a Creative Commons Attribution 4.0 International License