Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 LCFGraph

Source Notebook

Return the graph specified in Lederberg–Coxeter–Fruchte notation

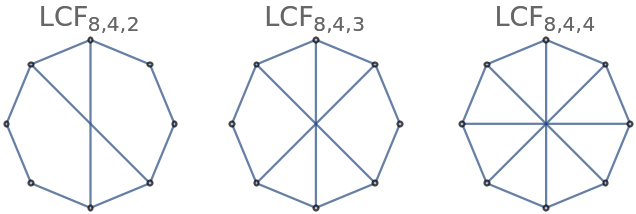
Contributed by: Alejandra Ortiz Duran

ResourceFunction["LCFGraph"][n,l,r]

returns the n vertex graph specified in LCF ([l]r) notation.

Details and Options

Lederberg-Coxeter-Fruchte (LCF) is a compressed notation used in the generation of various cubic Hamiltonian graphs of high symmetry. As a start, a cycle of size n is drawn. From there, the LCF code is used to move forward or back the given number of vertices. For example, with LCF code {4}2, two adjacent vertices are connected to the vertex forward four, twice.
LCFGraph is typically used to for the representation of cubic graphs that contain a Hamiltonian cycle.
ResourceFunction["LCFGraph"][n, l, r, DirectedEdges→True] gives a directed LCF graph.
ResourceFunction["LCFGraph"] generates a Graph object.
ResourceFunction["LCFGraph"] takes the same options as Graph.

Examples

Basic Examples (1) 

Generate the Nauru graph:

In[1]:=
ResourceFunction["LCFGraph"][24, {5, -9, 7, -7, 9, -5}, 4]
Out[1]=

Scope (2) 

LCFGraph works with undirected graphs:

In[2]:=
ResourceFunction["LCFGraph"][24, {5, -9, 7, -7, 9, -5}, 4]
Out[2]=

Directed graphs:

In[3]:=
ResourceFunction["LCFGraph"][24, {5, -9, 7, -7, 9, -5}, 4, DirectedEdges -> True]
Out[3]=

Options (11) 

AnnotationRules (2) 

Specify an annotation for vertices:

In[4]:=
ResourceFunction["LCFGraph"][10, {2}, 10, AnnotationRules -> {1 -> {VertexLabels -> "hello"}}]
Out[4]=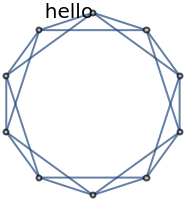

Edges:

In[5]:=
ResourceFunction["LCFGraph"][10, {2}, 10, AnnotationRules -> {1 \[UndirectedEdge] 2 -> {EdgeLabels -> "hello"}}]
Out[5]=

GraphHighlight (3) 

Highlight the vertex 1:

In[6]:=
ResourceFunction["LCFGraph"][10, {2}, 10, GraphHighlight -> {1}]
Out[6]=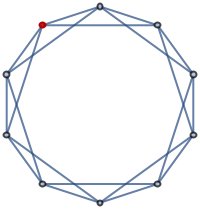

Highlight the edge 23:

In[7]:=
ResourceFunction["LCFGraph"][10, {2}, 10, GraphHighlight -> {2 \[UndirectedEdge] 3}]
Out[7]=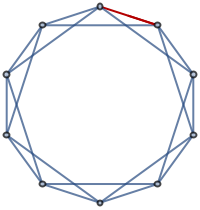

Highlight the vertices and edges:

In[8]:=
ResourceFunction["LCFGraph"][10, {2}, 10, GraphHighlight -> {1, 2, 1 \[UndirectedEdge] 3, 2 \[UndirectedEdge] 3}]
Out[8]=

PlotTheme (2) 

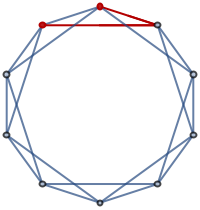Use a common base theme:

In[9]:=
ResourceFunction["LCFGraph"][10, {2}, 10, PlotTheme -> "Business"]
Out[9]=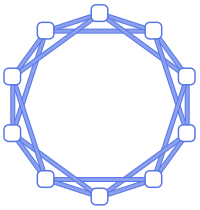

Use a monochrome theme:

In[10]:=
ResourceFunction["LCFGraph"][10, {2}, 10, PlotTheme -> "Monochrome"]
Out[10]=

VertexSize (3) 

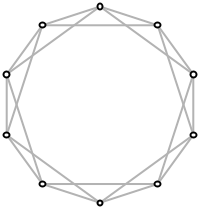By default, the size of vertices is computed automatically:

In[11]:=
ResourceFunction["LCFGraph"][10, {2}, 10, VertexSize -> Automatic]
Out[11]=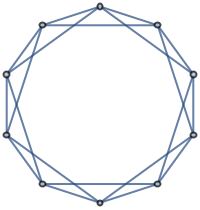

Specify the size of all vertices using symbolic vertex size:

In[12]:=
Table[ResourceFunction["LCFGraph"][10, {2}, 10, VertexSize -> s, PlotLabel -> s], {s, {Tiny, Small, Medium, Large}}]
Out[12]=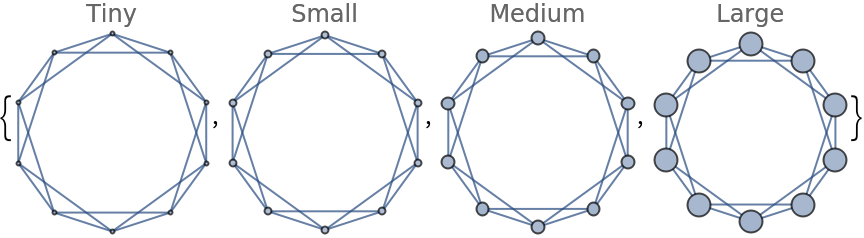

Specify the size for individual vertices:

In[13]:=
ResourceFunction["LCFGraph"][10, {2}, 10, VertexSize -> {1 -> 0.2, 2 -> 0.3}]
Out[13]=

VertexStyle (1) 

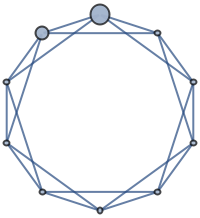Style individual vertices:

In[14]:=
ResourceFunction["LCFGraph"][10, {2}, 10, VertexStyle -> {1 -> Blue, 2 -> Red}, VertexSize -> 0.2, ImageSize -> 100]
Out[14]=

Applications (1) 

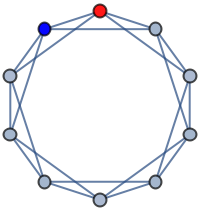Check the isomorphism of some of the standard known LCFGraphs:

In[15]:=
IsomorphicGraphQ[ResourceFunction["LCFGraph"][4, {2}, 4], GraphData["TetrahedralGraph"]]
Out[15]=
In[16]:=
IsomorphicGraphQ[ResourceFunction["LCFGraph"][6, {3}, 6], GraphData["UtilityGraph"]]
Out[16]=
In[17]:=
IsomorphicGraphQ[ResourceFunction["LCFGraph"][8, {3, -3}, 4], GraphData["CubicalGraph"]]
Out[17]=
In[18]:=
IsomorphicGraphQ[ResourceFunction["LCFGraph"][8, {4}, 8], GraphData["WagnerGraph"]]
Out[18]=
In[19]:=
IsomorphicGraphQ[ResourceFunction["LCFGraph"][8, {4, -3, 3, 4}, 2], GraphData["WagnerGraph"]]
Out[19]=
In[20]:=
IsomorphicGraphQ[ResourceFunction["LCFGraph"][12, {-5, -3, 3, 5}, 3], GraphData["FranklinGraph"]]
Out[20]=
In[21]:=
IsomorphicGraphQ[ ResourceFunction["LCFGraph"][ 12, {-5, -2, -4, 2, 5, -2, 2, 5, -2, -5, 4, 2}, 1], GraphData["FruchtGraph"]]
Out[21]=
In[22]:=
IsomorphicGraphQ[ResourceFunction["LCFGraph"][12, {2, 6, -2}, 4], GraphData["TruncatedTetrahedralGraph"]]
Out[22]=
In[23]:=
IsomorphicGraphQ[ResourceFunction["LCFGraph"][14, {-5, 5}, 7], GraphData["HeawoodGraph"]]
Out[23]=
In[24]:=
IsomorphicGraphQ[ ResourceFunction["LCFGraph"][18, {5, 7, -7, 7, -7, -5}, 3], GraphData["PappusGraph"]]
Out[24]=
In[25]:=
IsomorphicGraphQ[ResourceFunction["LCFGraph"][20, {5, -5, 9, -9}, 4], GraphData["DesarguesGraph"]]
Out[25]=
In[26]:=
IsomorphicGraphQ[ ResourceFunction["LCFGraph"][ 20, {10, 7, 4, -4, -7, 10, -4, 7, -7, 4}, 2], GraphData["DodecahedralGraph"]]
Out[26]=
In[27]:=
IsomorphicGraphQ[ResourceFunction["LCFGraph"][24, {12, 7, -7}, 8], GraphData["McGeeGraph"]]
Out[27]=
In[28]:=
IsomorphicGraphQ[ ResourceFunction["LCFGraph"][24, {2, 9, -2, 2, -9, -2}, 4], GraphData["TruncatedCubicalGraph"]]
Out[28]=
In[29]:=
IsomorphicGraphQ[ResourceFunction["LCFGraph"][24, {3, -7, 7, -3}, 6], GraphData["TruncatedOctahedralGraph"]]
Out[29]=
In[30]:=
IsomorphicGraphQ[ ResourceFunction["LCFGraph"][24, {5, -9, 7, -7, 9, -5}, 4], GraphData["NauruGraph"]]
Out[30]=
In[31]:=
IsomorphicGraphQ[ ResourceFunction["LCFGraph"][32, {5, -5, 13, -13}, 8], GraphData["DyckGraph"]]
Out[31]=
In[32]:=
IsomorphicGraphQ[ ResourceFunction["LCFGraph"][ 60, {30, \[Minus]2, 2, 21, \[Minus]2, 2, 12, \[Minus]2, 2, \[Minus]12, \[Minus]2, 2, \[Minus]21, \[Minus]2, 2, 30, \[Minus]2, 2, \[Minus]12, \[Minus]2, 2, 21, \[Minus]2, 2, \[Minus]21, \[Minus]2, 2, 12, \[Minus]2, 2}, 2], GraphData["TruncatedDodecahedralGraph"]]
Out[32]=
In[33]:=
IsomorphicGraphQ[ ResourceFunction["LCFGraph"][ 70, {\[Minus]29, \[Minus]19, \[Minus]13, 13, 21, \[Minus]27, 27, 33, \[Minus]13, 13, 19, \[Minus]21, \[Minus]33, 29}, 5], GraphData["HarriesGraph"]]
Out[33]=
In[34]:=
IsomorphicGraphQ[ ResourceFunction["LCFGraph"][ 112, {47, \[Minus]23, \[Minus]31, 39, 25, \[Minus]21, \[Minus]31, \[Minus]41, 25, 15, 29, \[Minus]41, \[Minus]19, 15, \[Minus]49, 33, 39, \[Minus]35, \[Minus]21, 17, \[Minus]33, 49, 41, 31, \[Minus]15, \[Minus]29, 41, 31, \[Minus]15, \[Minus]25, 21, 31, \[Minus]51, \[Minus]25, 23, 9, \[Minus]17, 51, 35, \[Minus]29, 21, \[Minus]51, \[Minus]39, 33, \[Minus]9, \[Minus]51, 51, \[Minus]47, \[Minus]33, 19, 51, \[Minus]21, 29, 21, \[Minus]31, \[Minus]39}, 2], GraphData["LjubljanaGraph"]]
Out[34]=
In[35]:=
IsomorphicGraphQ[ ResourceFunction["LCFGraph"][ 126, {17, 27, \[Minus]13, \[Minus]59, \[Minus]35, 35, \[Minus]11, 13, \[Minus]53, 53, \[Minus]27, 21, 57, 11, \[Minus]21, \[Minus]57, 59, \[Minus]17}, 7], GraphData["Tutte12Cage"]]
Out[35]=

Requirements

Wolfram Language 13.0 (December 2021) or above

Version History

  • 1.0.0 – 21 October 2024

Related Resources

License Information