Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 ParetoPrinciplePlot

Source Notebook

Make Pareto principle adherence plots

Contributed by: Anton Antonov

ResourceFunction["ParetoPrinciplePlot"][vec]

plots the normalized cumulative sum of the reverse-sorted list vec.

Details and Options

The adherence of the data vec to the Pareto principle can be easily verified with the plots of ResourceFunction["ParetoPrinciplePlot"].
The argument can be a numerical list, a list of numerical lists or a list of numerical lists wrapped with tooltips and callouts.
For a given numerical vector vec, the Pareto principle plot data is computed with the formula: Accumulate[ReverseSort[vec]]/Total[vec].
ResourceFunction["ParetoPrinciplePlot"] accepts all options of ListPlot, with the following additions:
"ParetoGridLines"Automaticshow Pareto-specific grid lines.
"Tooltip"Truewhether automatic Tooltip wrappers should be used
The option "ParetoGridLines" can be used to define Pareto principle–specific grid lines.
The option "Tooltip" can be used to specify the use of automatic Tooltip wrappers.

Examples

Basic Examples (2) 

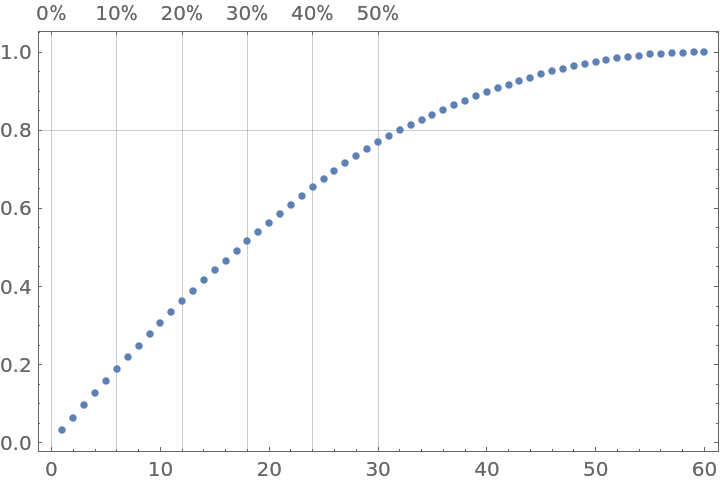
Pareto principle plot for a numerical vector:

In[1]:=
SeedRandom[2723]; ResourceFunction["ParetoPrinciplePlot"][RandomReal[1, 60]]
Out[2]=

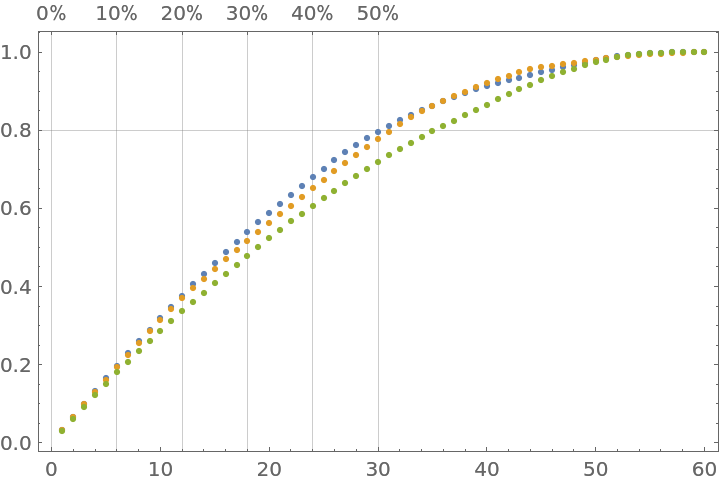
Pareto principle plot for a list of numerical vectors:

In[3]:=
SeedRandom[574]; ResourceFunction["ParetoPrinciplePlot"][RandomReal[1, {3, 60}]]
Out[4]=

Scope (3) 

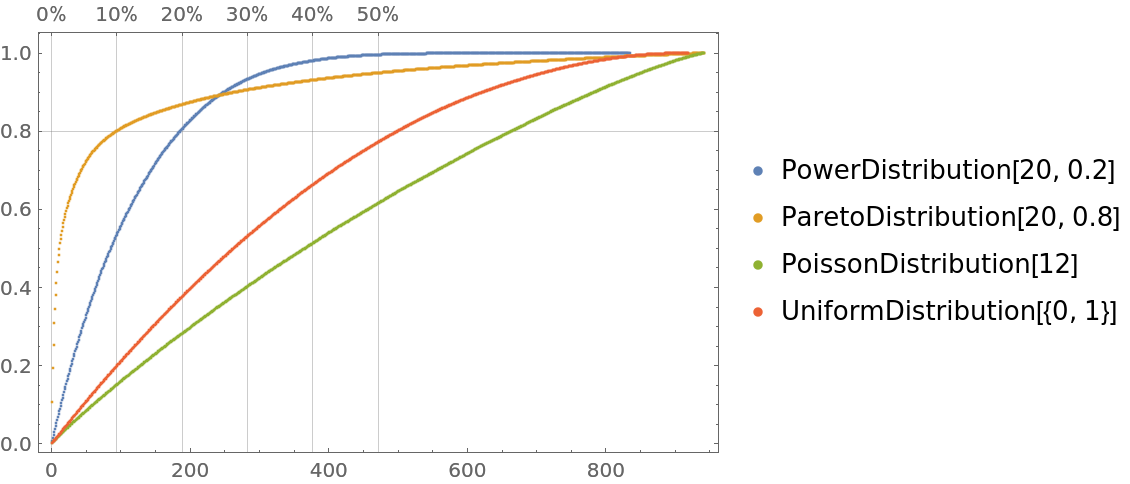
Plot a list of numerical vectors with tooltips:

In[5]:=
dists = {PowerDistribution[20, 0.2], ParetoDistribution[20, 0.8], PoissonDistribution[12], UniformDistribution[]}; ResourceFunction[ "ParetoPrinciplePlot"][ Tooltip[RandomVariate[#, RandomInteger[{800, 1000}]], #] & /@ dists, PlotRange -> All, PlotLegends -> dists]
Out[5]=

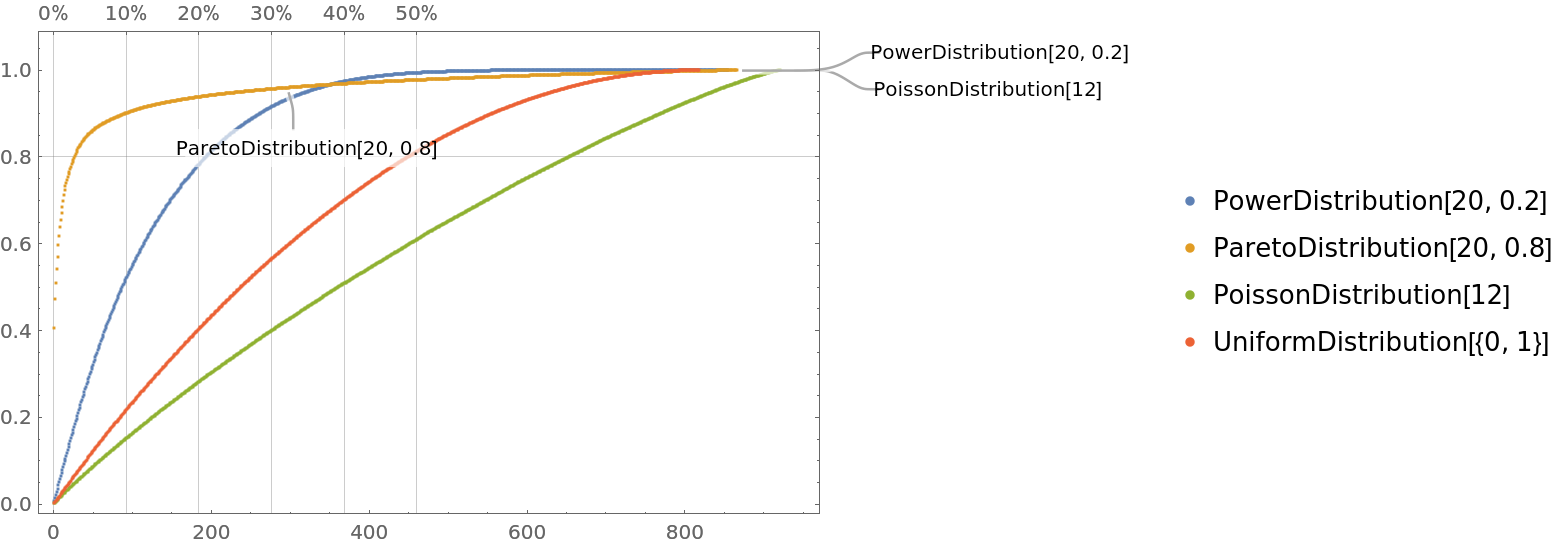
Numerical vectors with nested Tooltip and Callout specifications can be given; "wrapped" and "plain" vectors can be mixed:

In[6]:=
data = Map[ Switch[#, _ParetoDistribution, Tooltip[ Callout[RandomVariate[#, RandomInteger[{800, 1000}]], #, {300, Below}], #], _UniformDistribution, RandomVariate[#, RandomInteger[{800, 1000}]], _, Callout[ Tooltip[RandomVariate[#, RandomInteger[{800, 1000}]], #], #] ] &, dists];
In[7]:=
dists = {PowerDistribution[20, 0.2], ParetoDistribution[20, 0.8], PoissonDistribution[12], UniformDistribution[]}; ResourceFunction["ParetoPrinciplePlot"][data, PlotLegends -> dists, ImageSize -> Large, PlotRange -> All]
Out[8]=

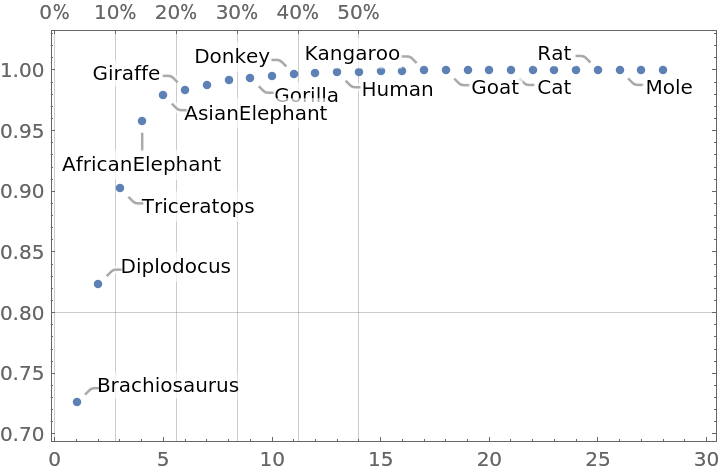
Plot an association with numerical values:

In[9]:=
data = <|"Brachiosaurus" -> 87000, "Diplodocus" -> 11700, "Triceratops" -> 9400, "AfricanElephant" -> 6654, "AsianElephant" -> 2547, "Giraffe" -> 529, "Horse" -> 521, "Cow" -> 465, "Gorilla" -> 207, "Pig" -> 192, "Donkey" -> 187.1`, "Jaguar" -> 100, "Human" -> 62, "Sheep" -> 55.5`, "Chimpanzee" -> 52.16`, "GreyWolf" -> 36.33`, "Kangaroo" -> 35, "Goat" -> 27.66`, "PotarMonkey" -> 10, "RhesusMonkey" -> 6.8`, "Cat" -> 3.3`, "Rabbit" -> 2.5`, "MountainBeaver" -> 1.35`, "GuineaPig" -> 1.04`, "Rat" -> 0.28`, "Mole" -> 0.122`, "GoldenHamster" -> 0.12`, "Mouse" -> 0.023`|>; ResourceFunction["ParetoPrinciplePlot"][data]
Out[10]=

Options (3) 

ParetoGridLines

A data vector:

In[11]:=
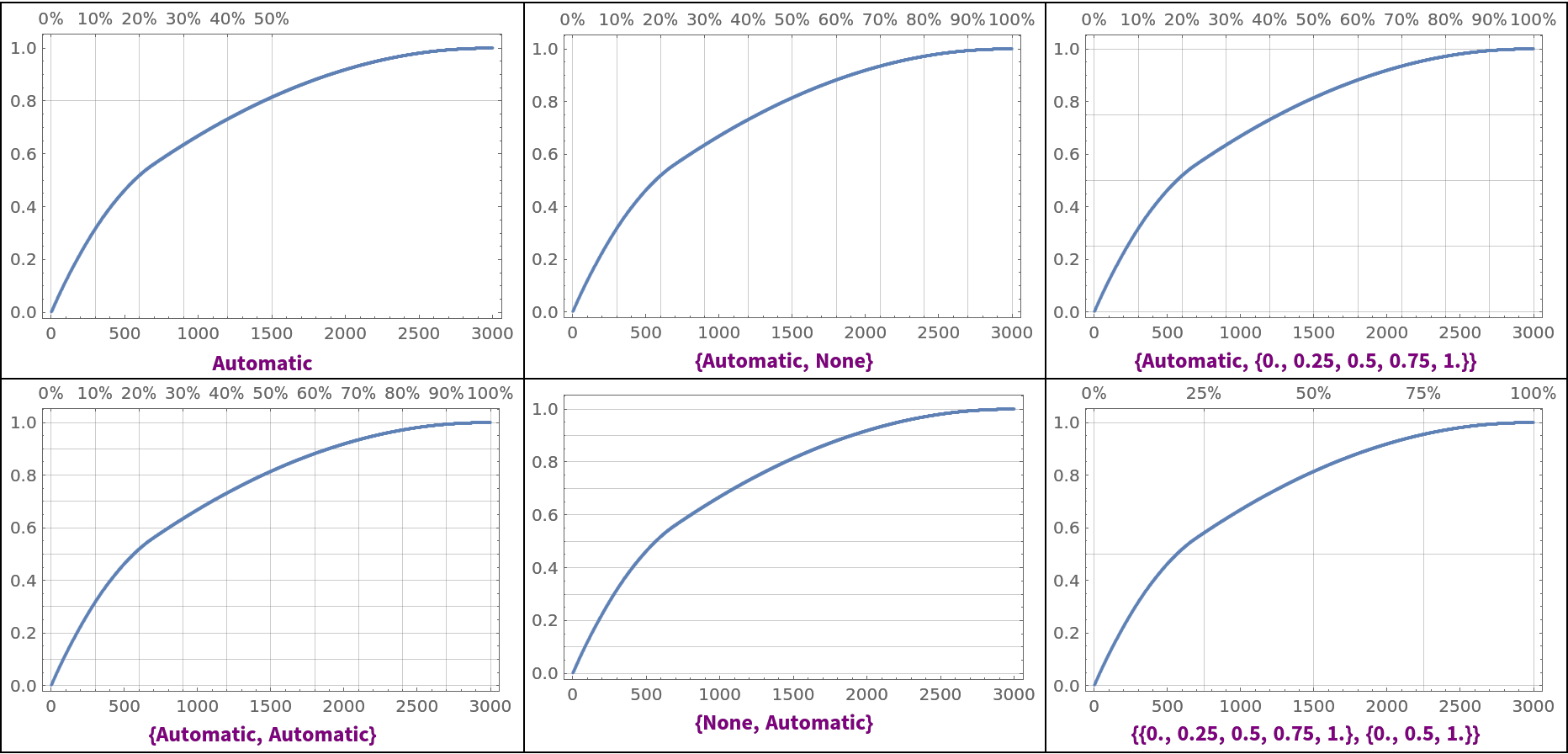
SeedRandom[232]; data = Join[RandomReal[1, 1000], RandomReal[{0, 0.3}, 2000]];

Pareto principle adherence plots with different Pareto grid lines specifications:

In[12]:=
Multicolumn[ Map[Labeled[ ResourceFunction["ParetoPrinciplePlot"][data, ImageSize -> 300, "ParetoGridLines" -> #], Style[#, Purple, Bold]] &, {Automatic, {Automatic, Automatic}, {Automatic, None}, {None, Automatic}, {Automatic, Range[0, 1, 0.25]}, {Range[0, 1, 0.25], Range[0, 1, 0.5]}}], 3, Dividers -> All]
Out[12]=

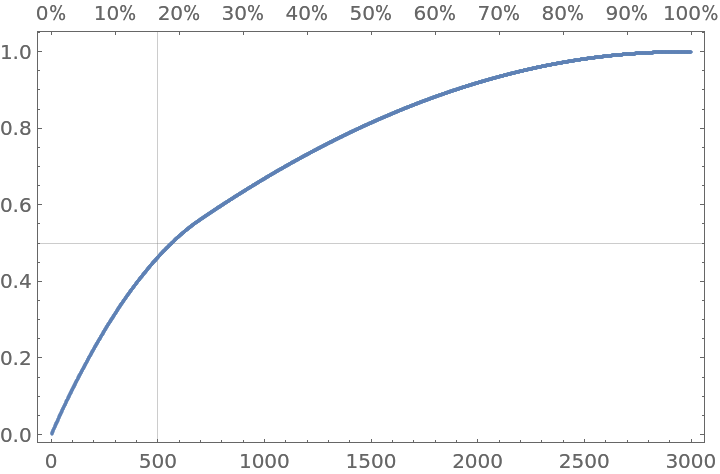
The option "ParetoGridLines" is overridden by the ListPlot option GridLines:

In[13]:=
ResourceFunction["ParetoPrinciplePlot"][data, "ParetoGridLines" -> {Automatic, Automatic}, GridLines -> {{500}, {0.5}}]
Out[13]=

Tooltip

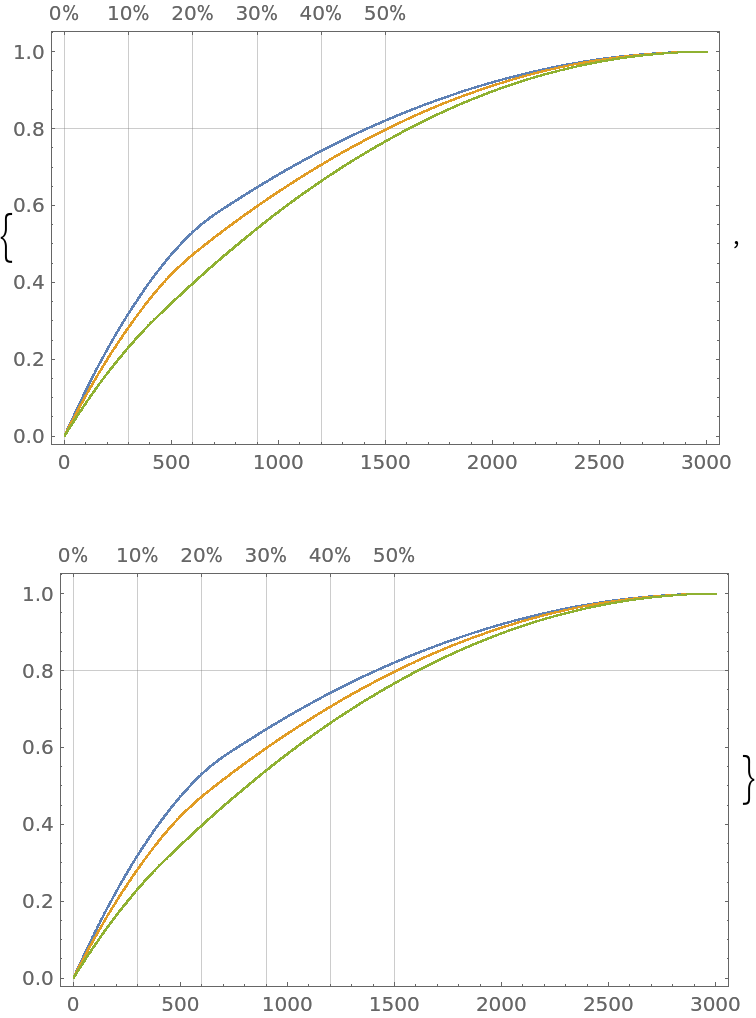
The option "Tooltip" takes Boolean values:

In[14]:=
SeedRandom[2323]; data = Table[ Join[RandomReal[1, 1000], RandomReal[{0, h}, 2000]], {h, {0.3, 0.4, 0.6}}];
In[15]:=
ResourceFunction["ParetoPrinciplePlot"][data, ImageSize -> Medium, "Tooltip" -> #] & /@ {False, True}
Out[15]=

Applications (7) 

Words distribution in texts (3) 

Get the text of Shakespeare’s play Hamlet:

In[16]:=
text = ResourceData["Hamlet"];

Convert the text to lowercase and split it into words:

In[17]:=
words = Select[ StringSplit[ ToLowerCase[text], {" ", ",", ".", ";", "?", "!", "...", "-"}], StringLength[#] > 0 &]; Length[words]
Out[18]=

Plot the words' tally values:

In[19]:=
ResourceFunction["ParetoPrinciplePlot"][Tally[words][[All, 2]]]
Out[19]=

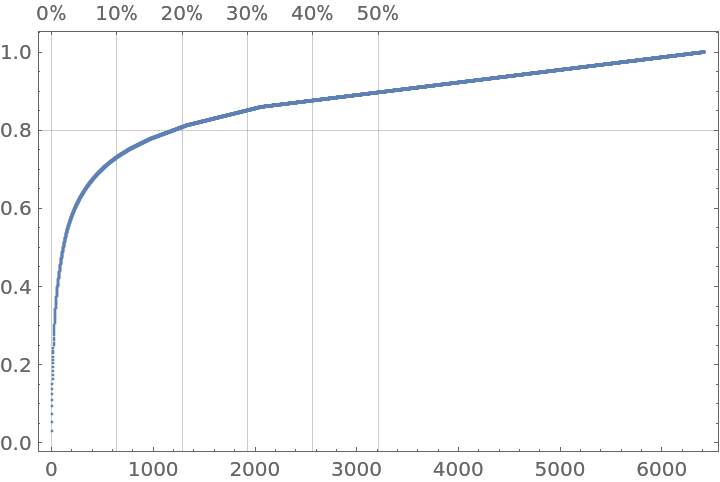
In the preceding Pareto principle adherence plot, you can see a clear Pareto principle manifestation: ≈15% of the words correspond to ≈80% of the text.

Gross Domestic Product (GDP) of countries (2) 

Pareto principle manifestation for countries' GDP, showing that ≈10% of the countries correspond to ≈80% of the total GDP:

In[20]:=
ResourceFunction["ParetoPrinciplePlot"][ QuantityMagnitude[ DeleteMissing[CountryData[#, "GDP"] & /@ CountryData["Countries"]]]]
Out[20]=

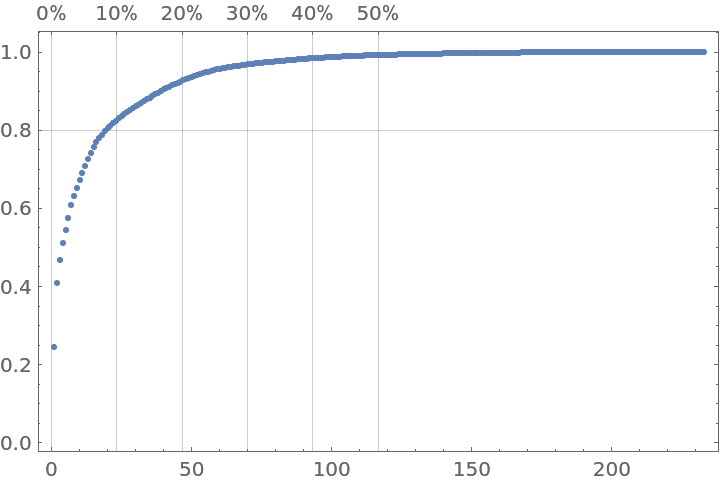
Plot together the curves of GDP changes for different countries in the same time period, demonstrating the rapid growth of China and Poland:

In[21]:=
res = Table[(t = CountryData[countryName, {{"GDP"}, {1970, 2019}}]; t = Reverse@Sort[t["Path"][[All, 2]] /. Quantity[x_, _] :> x]; Tooltip[t, countryName]), {countryName, {"USA", "China", "Poland", "Germany", "France", "Denmark"}}]; ResourceFunction["ParetoPrinciplePlot"][res, PlotRange -> All, Joined -> True, PlotLegends -> res[[All, 2]]]
Out[22]=

Lake data (2) 

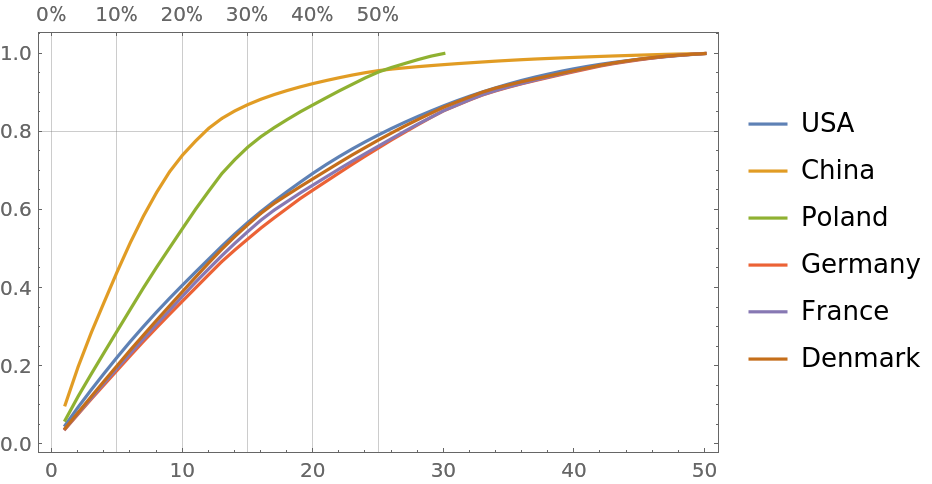
Gather data for lakes and make Pareto principle plots for the lakes' surface areas, volumes and fish catch:

In[23]:=
lakeAreas = LakeData[All, "SurfaceArea"]; lakeVolumes = LakeData[All, "Volume"]; lakeFishCatch = LakeData[All, "CommercialFishCatch"];
In[24]:=
data = {lakeAreas, lakeVolumes, lakeFishCatch}; t = N@Map[QuantityMagnitude@*DeleteMissing, data];

You can see that the lakes' area data manifests an “exaggerated” Pareto principle adherence; ≈5% of the lakes correspond to ≈90% of the total lake area:

In[25]:=
opts = {PlotRange -> All, ImageSize -> Medium}; MapThread[ ResourceFunction["ParetoPrinciplePlot"][#1, PlotLabel -> Row[{#2, ", ", #3}], opts] &, {t, {"Lake area", "Lake volume", "Commercial fish catch"}, DeleteMissing[#][[1, 2]] & /@ data}]
Out[25]=

Properties and Relations (2) 

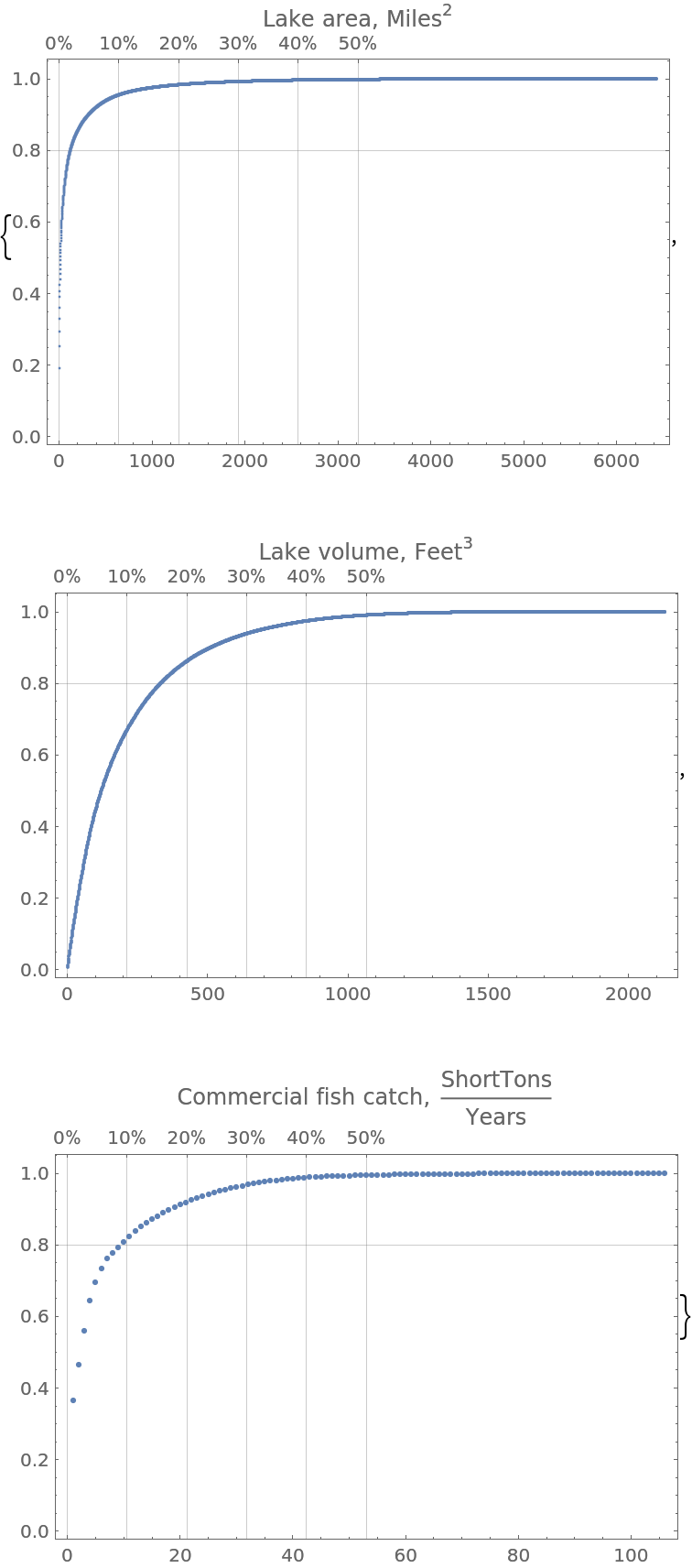
A numeric vector:

In[26]:=
vec = RandomReal[1, 1000];

The Pareto principle plot data is computed using the following formula:

In[27]:=
pvec = Accumulate[ReverseSort[vec]]/Total[vec];

Show the corresponding plot:

In[28]:=
ListPlot[pvec, PlotTheme -> "Detailed"]
Out[28]=

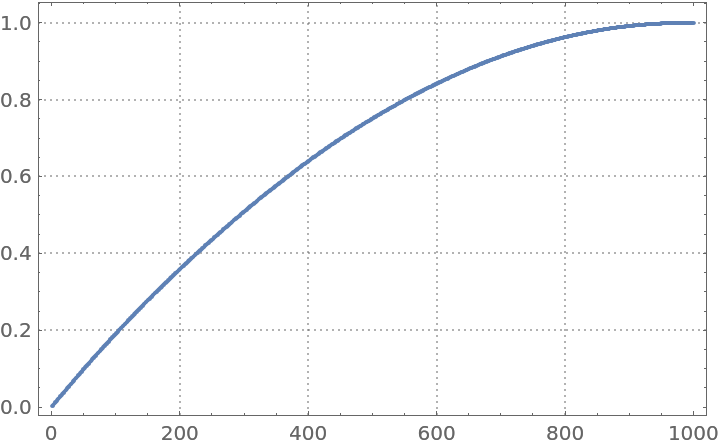
Compare with the plot made by ParetoPrinciplePlot:

In[29]:=
ResourceFunction["ParetoPrinciplePlot"][vec]
Out[29]=

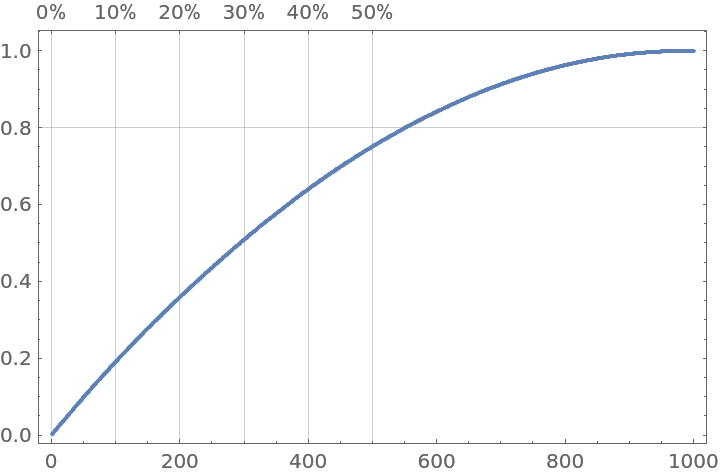
It is beneficial to use Pareto principle adherence plots together with data summaries and histograms:

In[30]:=
vec = QuantityMagnitude[DeleteMissing[LakeData[All, "SurfaceArea"]]]; opts = {PlotTheme -> "Detailed", ImageSize -> 300};

Note that the summary and histograms provide complementary data distribution properties to those given by the Pareto principle adherence plot:

In[31]:=
Grid[{ {ResourceFunction["ParetoPrinciplePlot"][vec, PlotLabel -> "Pareto principle adherence", opts], Labeled[ResourceFunction["RecordsSummary"][vec], "Summary", Top]}, {Histogram[vec, Automatic, "Probability", PlotLabel -> "Direct histtogram", opts], Histogram[Log10@vec, Automatic, "Probability", PlotLabel -> "\!\(\*SubscriptBox[\(Log\), \(10\)]\) histogram", opts]}}, Dividers -> All]
Out[31]=

Possible Issues (2) 

Missing values (2) 

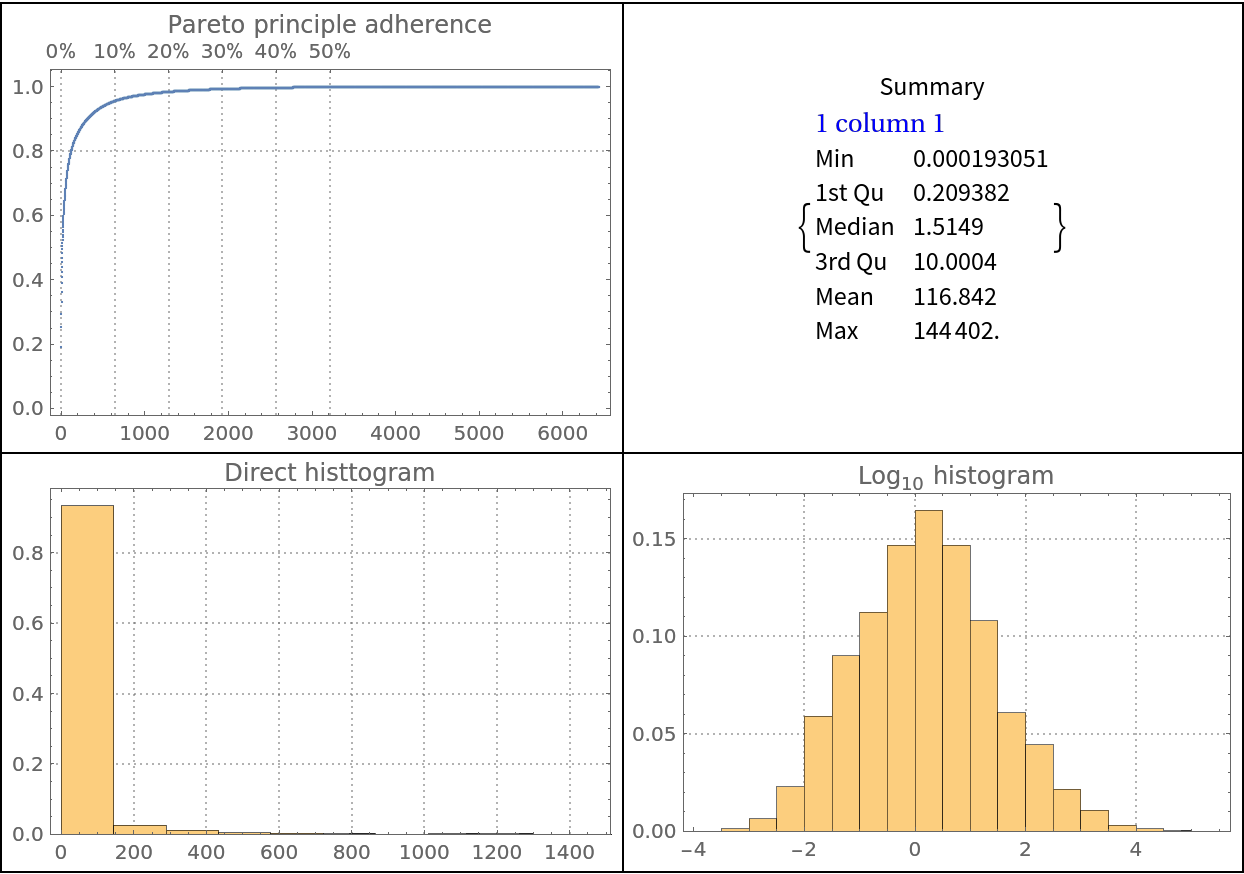
ParetoPrinciplePlot does not work on vectors with missing values:

In[32]:=
ResourceFunction[ "ParetoPrinciplePlot"][{Missing[], 10, 1, 20, 10, 12, 2, 7}]
Out[32]=

Use DeleteMissing to obtain a plot:

In[33]:=
ResourceFunction["ParetoPrinciplePlot"][ DeleteMissing[{Missing[], 10, 1, 20, 10, 12, 2, 7}]]
Out[33]=

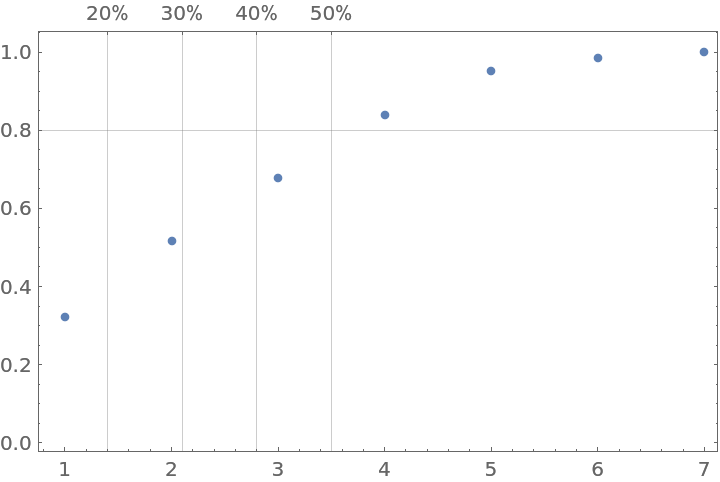
ParetoPrinciplePlot does not work on QuantityArray objects and lists of Quantity objects:

In[34]:=
Shallow[DeleteMissing[lakeAreas = LakeData[All, "SurfaceArea"]]]
Out[34]=
In[35]:=
ResourceFunction["ParetoPrinciplePlot"][DeleteMissing[lakeAreas]]
Out[35]=

Use DeleteMissing and QuantityMagnitude to obtain a plot:

In[36]:=
ResourceFunction["ParetoPrinciplePlot"][ QuantityMagnitude[DeleteMissing[lakeAreas]]]
Out[36]=

Neat Examples (1) 

Pareto principle adherence plots for word tallies for different translations of the United Nations’ "Universal Declaration of Human Rights" official document:

In[37]:=
GetWords[text_String] := Select[StringSplit[ ToLowerCase[text], {" ", ",", ".", ";", "?", "!", "...", "-"}], StringLength[#] > 0 &]; textIDs = Select[ExampleData["Text"], StringMatchQ[#[[2]], "UNHuman" ~~ __] &]; textNames = StringTake[#[[2]], {StringLength["UNHumanRights"] + 1, -1}] & /@ textIDs; textData = MapThread[ Tooltip[Tally[GetWords[ExampleData[#1]]][[All, 2]], #2] &, {textIDs, textNames}]; textK = 0; textData = Map[If[MemberQ[{"English", "Hawaiian", "Japanese", "Korean", "Latin", "Maori", "Russian"}, #[[2]]], Callout[#, #[[2]], {100 + 35*(textK++), Below}], #] &, textData]; ResourceFunction["ParetoPrinciplePlot"][textData, "ParetoGridLines" -> {Automatic, Automatic}, PlotLegends -> textNames, Joined -> True, ImageSize -> Large, PlotLabel -> Style["Pareto principle adherence for word tallies of\n\"UN Human Rights\" in different languages\n", Bold, Purple, FontSize -> 14]]
Out[43]=

Publisher

Anton Antonov

Version History

  • 1.0.1 – 28 June 2021
  • 1.0.0 – 13 December 2019

Source Metadata

  • Citation:
    https://en.wikipedia.org/wiki/Pareto_principle

Related Resources

License Information