Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Encode an SK combinator expression into a list of 0s and 1s
ResourceFunction["CombinatorEncode"][comb] encodes the combinator expression comb (composed of the symbols s and k) as a list of 0s and 1s. | |
ResourceFunction["CombinatorEncode"][comb, fmt] yields the encoding of comb in the format fmt. |
| 00 | |
| 01 | |
| 1 |
| CombinatorSymbols | Automatic | which combinator symbols should be used instead of s and k |
Encode a combinator expression into a unique list of 1s and 0s:
| In[1]:= |
|
| Out[1]= |
|
Return the result of the encoding in various formats:
| In[2]:= |
|
| Out[2]= |
|
Specify which combinator symbols to encode instead of s and k:
| In[3]:= |
|
| Out[3]= |
|
Encode the five combinators that appear in Schönfinkel’s original paper:
| In[4]:= |
![With[{cexpr = {\[FormalS], \[FormalK], \[FormalS][\[FormalK]][\[FormalK]], \[FormalS][\[FormalK][\[FormalS]]][\[FormalK]], \[FormalS][\[FormalS][\[FormalK][\[FormalS][\[FormalK][\[FormalS]]][\[FormalK]]]][\[FormalS]]][\[FormalK][\[FormalK]]]}},
TableForm[
Transpose[{cexpr, Sequence @@ ResourceFunction["CombinatorEncode"][cexpr, {String, Number}]}],
TableHeadings -> {
{"S (fusion)", "K (constancy)", "I (identity)", "B (composition)",
"C (interchange)"},
{"Expression", "EncodedBinaryString", "EncodedDecimal"}}]
]](https://www.wolframcloud.com/obj/resourcesystem/images/862/86237fcd-513c-4d61-a0ad-a639927f42ce/4fa9255ba821a5c2.png)
|
| Out[4]= |

|
Define a function for visualizing encodings:
Visualize states of a multiway combinator evaluation graph:
| In[5]:= |
![ResourceFunction["MultiwayCombinator"][
{\[FormalS][x_][y_][z_] :> x[z][y[z]], \[FormalK][x_][y_] :> x}, \[FormalS][\[FormalK][\[FormalS]][\[FormalS][\[FormalK]][\[FormalK]]]][\[FormalS][\[FormalK]][\[FormalK]][\[FormalS][\[FormalK]][\[FormalK]]]],
6, "StatesGraph", "StateRenderingFunction" -> encodeStateF]](https://www.wolframcloud.com/obj/resourcesystem/images/862/86237fcd-513c-4d61-a0ad-a639927f42ce/38277b6087f314e5.png)
|
| Out[5]= |

|
Plot the contraction of the Ω term, which reduces to itself after three steps:
| In[6]:= |
![clRules = {
\[FormalK][x_][y_] :> x,
\[FormalS][x_][y_][z_] :> x[z][y[z]]
};
\[CapitalOmega] = \[FormalS][i][i][\[FormalS][i][i]] /. i -> \[FormalS][\[FormalK]][\[FormalK]];
ArrayPlot[
ResourceFunction["CombinatorEncode"][
NestList[# /. clRules &, \[CapitalOmega], 30]], Mesh -> All]](https://www.wolframcloud.com/obj/resourcesystem/images/862/86237fcd-513c-4d61-a0ad-a639927f42ce/619480f5b98bf3ba.png)
|
| Out[8]= |
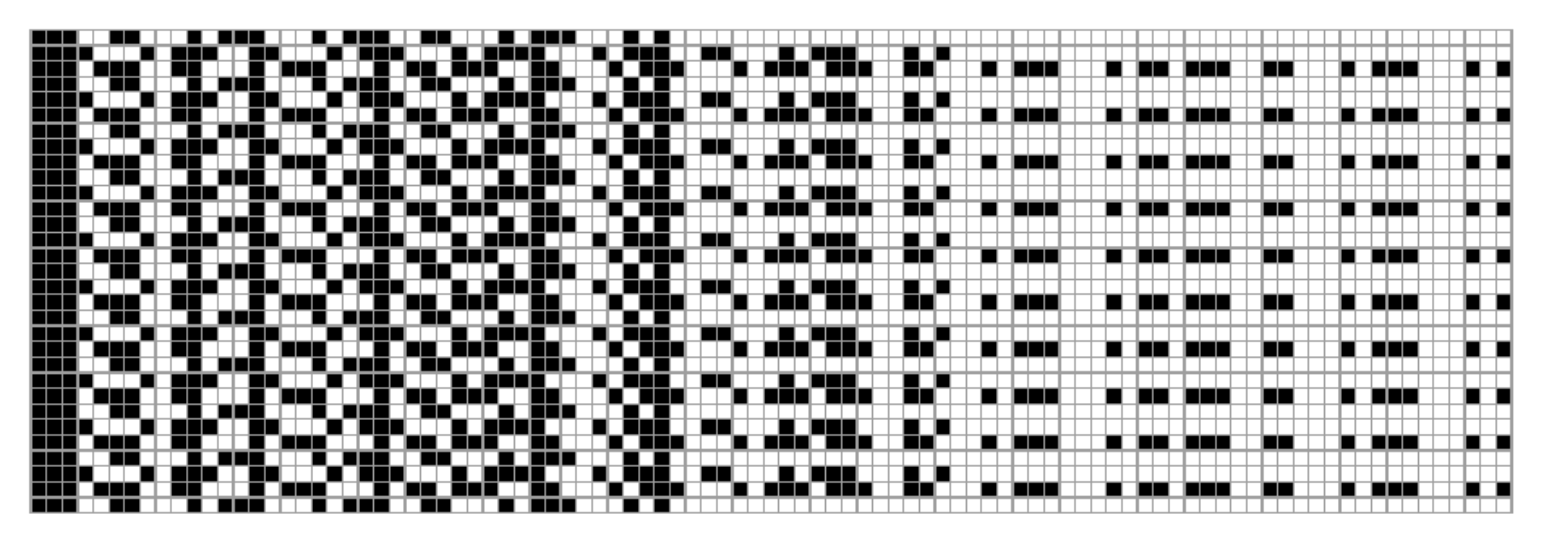
|
Plot the successive applications of the successor function s[b] starting with k[i] (0):
| In[9]:= |
![clRulesExtended = {
\[FormalK][x_][y_] :> x,
\[FormalS][x_][y_][z_] :> x[z][y[z]],
i -> \[FormalS][\[FormalK]][\[FormalK]],
b -> \[FormalS][\[FormalK][\[FormalS]]][\[FormalK]]
};
ArrayPlot[
PadLeft[
ResourceFunction["CombinatorEncode"][
NestList[\[FormalS][b][#] //. clRulesExtended &, \[FormalK][i] /. clRulesExtended, 20]],
Automatic,
-1],
ColorRules -> {0 -> Gray, -1 -> White}, AspectRatio -> 1/2]](https://www.wolframcloud.com/obj/resourcesystem/images/862/86237fcd-513c-4d61-a0ad-a639927f42ce/67c4300045663bdb.png)
|
| Out[10]= |
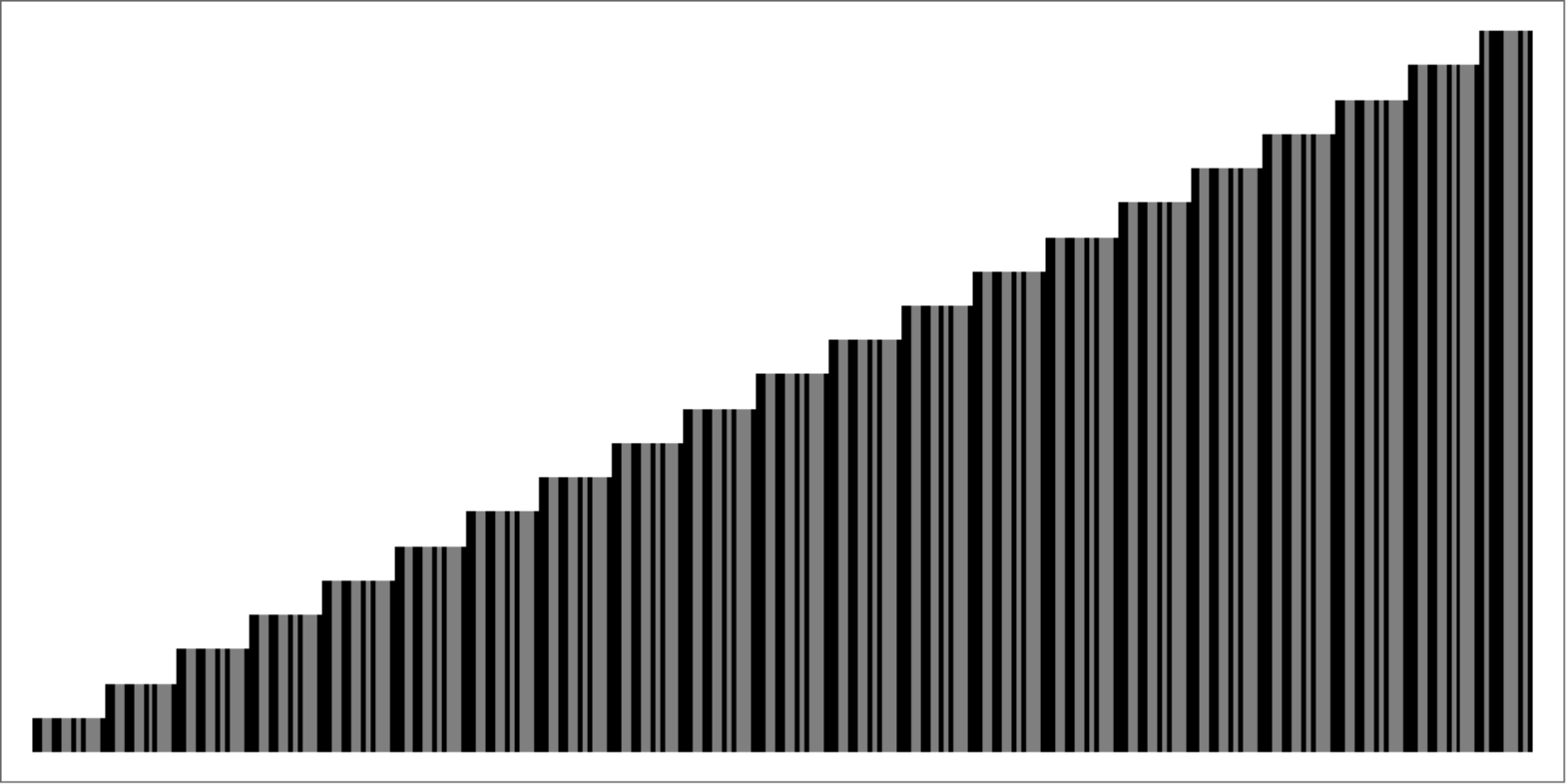
|
Unknown symbols in the expression cannot be encoded:
| In[11]:= |
|
| Out[11]= |
|
| In[12]:= |
|
| Out[12]= |
|
This work is licensed under a Creative Commons Attribution 4.0 International License