Function Repository Resource:

CombinatorEncode

Source Notebook

Encode an SK combinator expression into a list of 0s and 1s

Contributed by: Daniel Sanchez

ResourceFunction["CombinatorEncode"][comb]

encodes the combinator expression comb (composed of the symbols s and k) as a list of 0s and 1s.

ResourceFunction["CombinatorEncode"][comb, fmt]

yields the encoding of comb in the format fmt.

Details and Options

The encoding (as a binary string)

of a combinator c is defined as:

ResourceFunction["CombinatorEncode"][{comb₁, comb₂, …}] returns the encoding of each combinator.

Valid formats fmt include "Color", List, Number and String.

ResourceFunction["CombinatorEncode"][expr,{fmt₁, fmt₂, …}] returns a list of differently formatted encoded expressions.

ResourceFunction["CombinatorEncode"] has the following option:

CombinatorSymbols

Automatic

which combinator symbols should be used instead of s and k

The value of CombinatorSymbols should be an Association of the form <|"CombinatorS"→s₁,"CombinatorK"→k₁|>, where the symbols s₁ and k₁ will be encoded instead of s and k, respectively.

Examples

Basic Examples (2)

Encode a combinator expression into a unique list of 1s and 0s:

In[1]:=

$ResourceFunction[ "CombinatorEncode"][\[FormalS][\[FormalK]][\[FormalK]]]$

Out[1]=

Return the result of the encoding in various formats:

In[2]:=

$ResourceFunction[ "CombinatorEncode"][\[FormalS][\[FormalK][\[FormalS]]][\[FormalK]], {"Color", List, Number, String}]$

Out[2]=

Options (1)

CombinatorSymbols (1)

Specify which combinator symbols to encode instead of s and k:

In[3]:=

Out[3]=

Applications (1)

Encode the five combinators that appear in Schönfinkel’s original paper:

In[4]:=

$With[{cexpr = {\[FormalS], \[FormalK], \[FormalS][\[FormalK]][\[FormalK]], \[FormalS][\[FormalK][\[FormalS]]][\[FormalK]], \[FormalS][\[FormalS][\[FormalK][\[FormalS][\[FormalK][\[FormalS]]][\[FormalK]]]][\[FormalS]]][\[FormalK][\[FormalK]]]}}, TableForm[ Transpose[{cexpr, Sequence @@ ResourceFunction["CombinatorEncode"][cexpr, {String, Number}]}], TableHeadings -> { {"S (fusion)", "K (constancy)", "I (identity)", "B (composition)", "C (interchange)"}, {"Expression", "EncodedBinaryString", "EncodedDecimal"}}] ]$

Out[4]=

Properties and Relations (2)

Define a function for visualizing encodings:

Visualize states of a multiway combinator evaluation graph:

In[5]:=

$ResourceFunction["MultiwayCombinator"][ {\[FormalS][x_][y_][z_] :> x[z][y[z]], \[FormalK][x_][y_] :> x}, \[FormalS][\[FormalK][\[FormalS]][\[FormalS][\[FormalK]][\[FormalK]]]][\[FormalS][\[FormalK]][\[FormalK]][\[FormalS][\[FormalK]][\[FormalK]]]], 6, "StatesGraph", "StateRenderingFunction" -> encodeStateF]$

Out[5]=

Neat Examples (2)

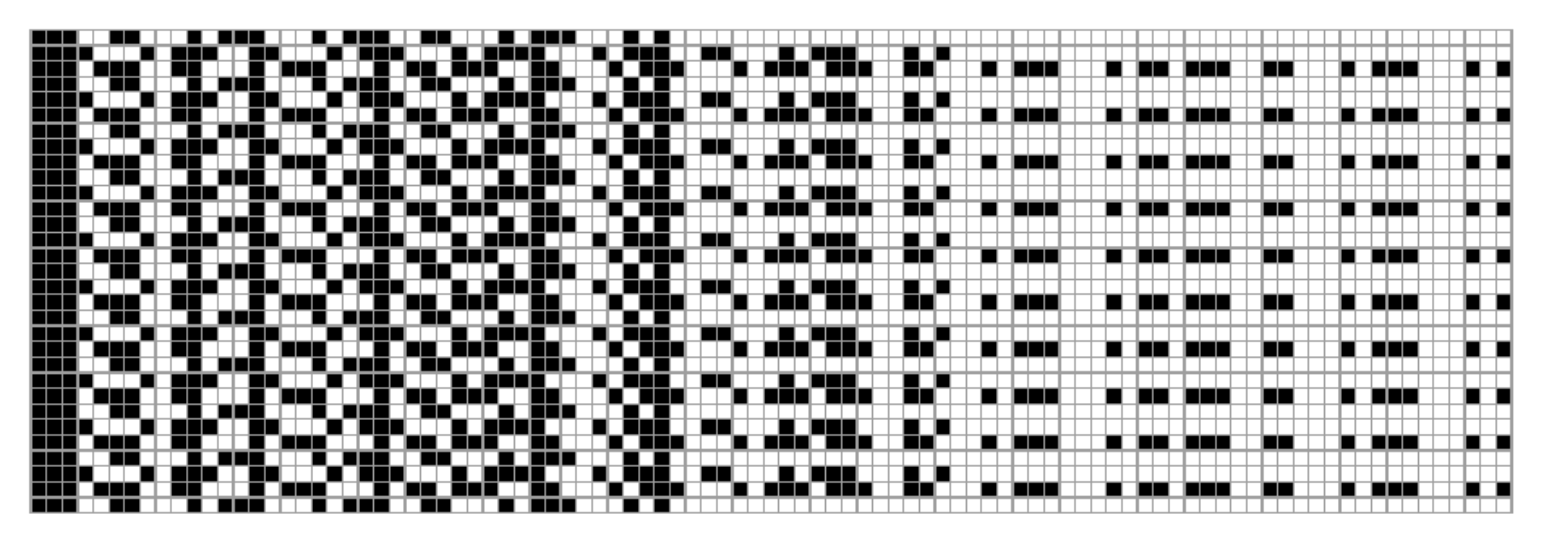
Plot the contraction of the Ω term, which reduces to itself after three steps:

In[6]:=

$clRules = { \[FormalK][x_][y_] :> x, \[FormalS][x_][y_][z_] :> x[z][y[z]] }; \[CapitalOmega] = \[FormalS][i][i][\[FormalS][i][i]] /. i -> \[FormalS][\[FormalK]][\[FormalK]]; ArrayPlot[ ResourceFunction["CombinatorEncode"][ NestList[# /. clRules &, \[CapitalOmega], 30]], Mesh -> All]$

Out[8]=

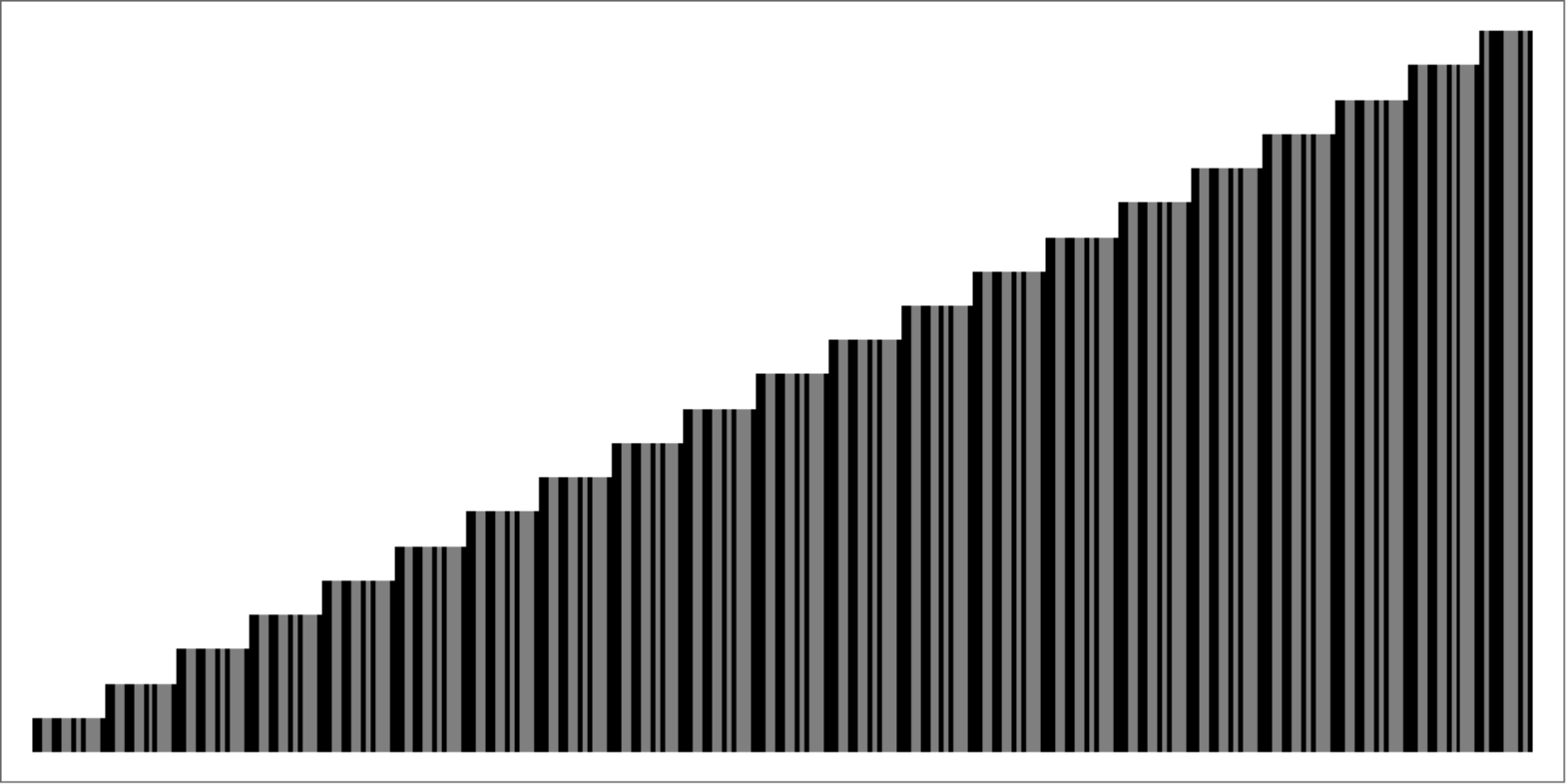
Plot the successive applications of the successor function s[b] starting with k[i] (0):

In[9]:=

$clRulesExtended = { \[FormalK][x_][y_] :> x, \[FormalS][x_][y_][z_] :> x[z][y[z]], i -> \[FormalS][\[FormalK]][\[FormalK]], b -> \[FormalS][\[FormalK][\[FormalS]]][\[FormalK]] }; ArrayPlot[ PadLeft[ ResourceFunction["CombinatorEncode"][ NestList[\[FormalS][b][#] //. clRulesExtended &, \[FormalK][i] /. clRulesExtended, 20]], Automatic, -1], ColorRules -> {0 -> Gray, -1 -> White}, AspectRatio -> 1/2]$