Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Generate points on a geodesic grid
ResourceFunction["GeodesicGridPoints"][n] attempts to arrange n points in a geodesic grid on a unit sphere centered at the origin. |
Generate 162 geodesic grid points:
| In[1]:= |
| Out[1]= | 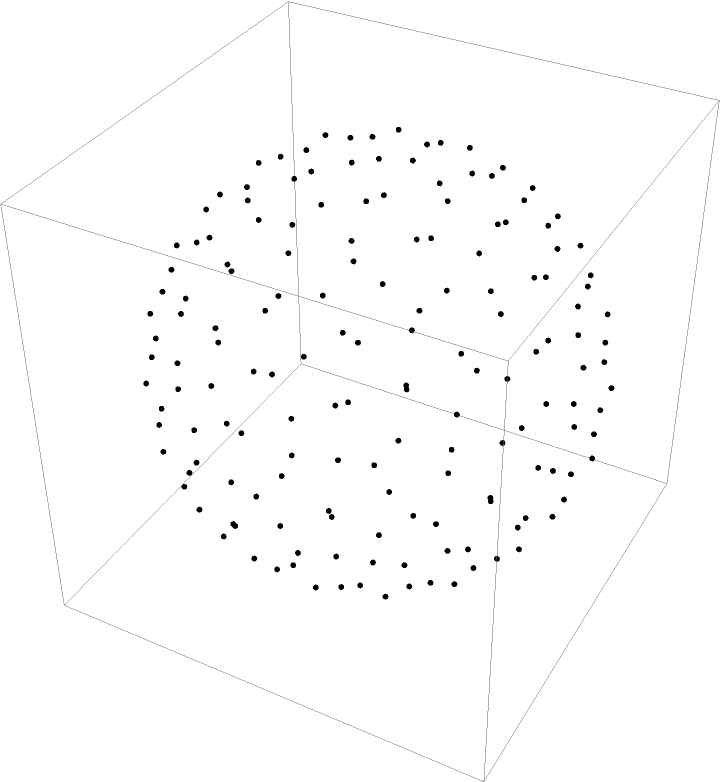 |
Generate machine-precision geodesic grid points:
| In[2]:= |
| Out[2]= |  |
Generate geodesic grid points with 24-digit precision:
| In[3]:= |
| Out[3]= |  |
Use a Delaunay mesh to make an approximation to a sphere:
| In[4]:= |
| Out[4]= |  |
Visualize the spherical Voronoi diagram of a set of geodesic grid points:
| In[5]:= | ![ResourceFunction["SphericalVoronoiDiagram"][
ResourceFunction["GeodesicGridPoints"][252], "ShowOriginalPoints" -> True]](https://www.wolframcloud.com/obj/resourcesystem/images/820/820ff594-ed86-4b33-bd8f-ed08ef78c69e/0a49e7ec822bbca6.png) |
| Out[5]= | 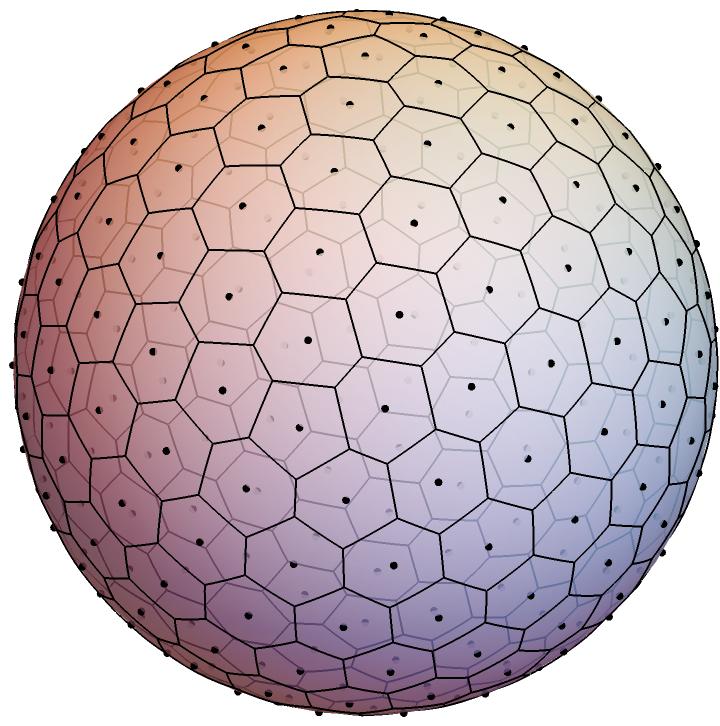 |
This work is licensed under a Creative Commons Attribution 4.0 International License