Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Calculate fractional integrals
ResourceFunction["FractionalIntegrate"][f,{x,α}] gives the α-fractional integral of the function f with respect to variable x. |
Semi-integral of 2x:
| In[1]:= |
| Out[1]= |
Taking the semi-integral twice yields the standard antiderivative:
| In[2]:= |
| Out[2]= |
If α=1, the result is the usual integral:
| In[3]:= |
| Out[3]= |
Semi-integral of elementary functions:
| In[4]:= |
| Out[4]= | 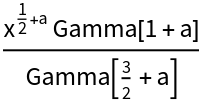 |
| In[5]:= |
| Out[5]= |
| In[6]:= |
| Out[6]= |
Semi-integral of trig functions:
| In[7]:= |
| Out[7]= |
| In[8]:= |
| Out[8]= |
Semi-integral of inverse trig functions:
| In[9]:= |
| Out[9]= |
| In[10]:= |
| Out[10]= |
More exotic fractional integrals:
| In[11]:= |
| Out[11]= | 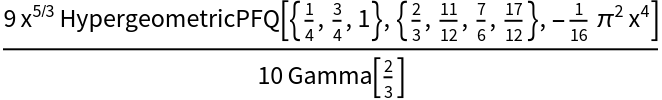 |
Not all integrals can be computed:
| In[12]:= |
| Out[12]= |
This work is licensed under a Creative Commons Attribution 4.0 International License