Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Compute a strophoid curve
ResourceFunction["StrophoidCurve"][c,p,f] computes one branch of the strophoid of the curve c with respect to the pole p and fixed point f. | |
ResourceFunction["StrophoidCurve"][c,p,f,-1] computes the other branch of the strophoid. |
One branch of the strophoid of a vertical line with fixed point at the origin, and pole at {1,0}:
| In[1]:= |
|
| Out[1]= |
|
The other branch of the strophoid:
| In[2]:= |
|
| Out[2]= |
|
Plot both branches together:
| In[3]:= |
|
| Out[3]= |
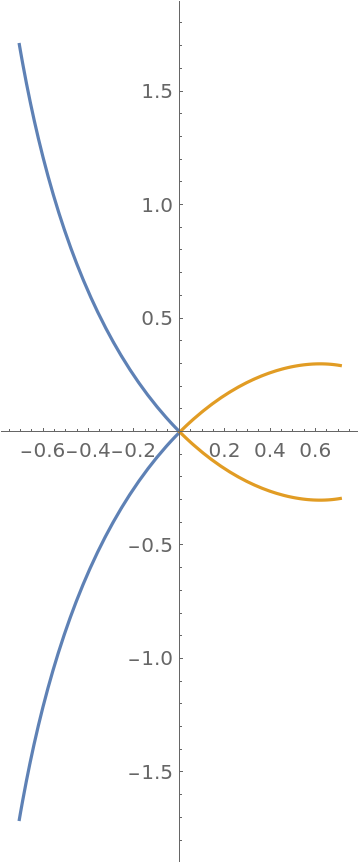
|
Find the implicit Cartesian equation of the strophoid:
| In[4]:= |
|
| Out[4]= |
|
The strophoid of a circle with pole at the circle's center, and fixed point at the circle's circumference:
| In[5]:= |
|
| Out[5]= |
|
Plot Freeth's nephroid:
| In[6]:= |
|
| Out[6]= |
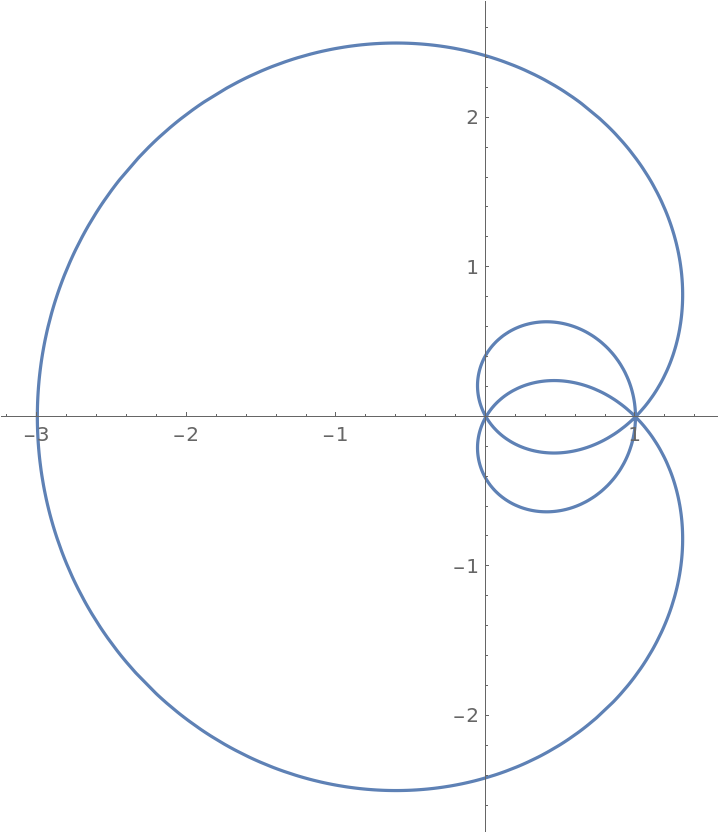
|
The strophoid of a limaçon with pole at the origin, and fixed point at the node of the limaçon:
| In[7]:= |
![freethSuper = ResourceFunction[
"StrophoidCurve"][{2 Cos[t] Cos[3 t], 2 Cos[t] Sin[3 t]}, {0, 0}, {-1, 0}] // Simplify // PowerExpand // FullSimplify](https://www.wolframcloud.com/obj/resourcesystem/images/81d/81def9aa-4e56-4d00-8a72-0ecee6acf03b/624792a08afcd2b6.png)
|
| Out[7]= |
|
Plot Freeth's supertrisectrix:
| In[8]:= |
|
| Out[8]= |
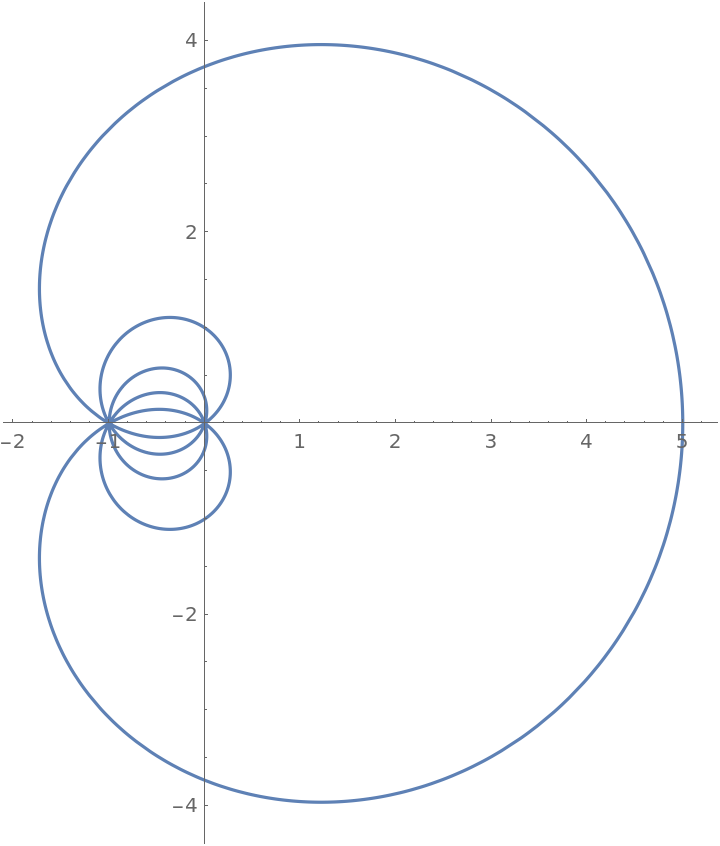
|
This work is licensed under a Creative Commons Attribution 4.0 International License