Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 NewtonCompanionMatrix

Source Notebook

Generate the companion matrix for the Newton interpolating polynomial of a given set of points

Contributed by: Jan Mangaldan

ResourceFunction["NewtonCompanionMatrix"][{f1,f2,…}]

yields the Newton companion matrix of an interpolating polynomial which reproduces the function values fi at successive integer values 1, 2, ….

ResourceFunction["NewtonCompanionMatrix"][{{x1,f1},{x2,f2},…}]

yields the Newton companion matrix of an interpolating polynomial for the function values fi corresponding to the abscissas xi.

ResourceFunction["NewtonCompanionMatrix"][{{{x1},f1,df1,…},…}]

yields the Newton companion matrix of an interpolating polynomial that reproduces derivatives as well as function values.

Details

ResourceFunction["NewtonCompanionMatrix"][data] gives an upper Hessenberg matrix whose characteristic polynomial is a scalar multiple of InterpolatingPolynomial[data,x].
The result of ResourceFunction["NewtonCompanionMatrix"] is a SparseArray.
With a list of data of length n, ResourceFunction["NewtonCompanionMatrix"] gives a square matrix with dimensions less than or equal to n-1.

Examples

Basic Examples (2) 

Construct the Newton companion matrix for the squares:

In[1]:=
ResourceFunction["NewtonCompanionMatrix"][{1, 4, 9}] // MatrixForm
Out[1]=

Check its characteristic polynomial:

In[2]:=
CharacteristicPolynomial[%, x]
Out[2]=

Construct the Newton companion matrix corresponding to an interpolating polynomial through three points:

In[3]:=
ResourceFunction[ "NewtonCompanionMatrix"][{{-1, 4}, {0, 2}, {1, 6}}] // MatrixForm
Out[3]=

The characteristic polynomial is a scalar multiple of the corresponding interpolating polynomial:

In[4]:=
CharacteristicPolynomial[%, x]
Out[4]=
In[5]:=
Expand[(#/Coefficient[#, x, Exponent[#, x]]) &[ InterpolatingPolynomial[{{-1, 4}, {0, 2}, {1, 6}}, x]]]
Out[5]=

Scope (2) 

Newton companion matrix for symbolic points:

In[6]:=
ResourceFunction[ "NewtonCompanionMatrix"][{{x1, y1}, {x2, y2}, {x3, y3}}] // MatrixForm
Out[6]=

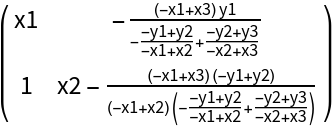
Construct the Newton companion matrix for points with derivative information supplied:

In[7]:=
ResourceFunction[ "NewtonCompanionMatrix"][{{{-1}, 4, 0}, {{0}, 2, -3}, {1, 6}}] // MatrixForm
Out[7]=

Applications (2) 

Find the roots of an interpolating polynomial by computing the eigenvalues of a Newton companion matrix:

In[8]:=
Eigenvalues[ N[ResourceFunction[ "NewtonCompanionMatrix"][{{{-1}, 4, 0}, {{0}, 2, -3}, {1, 6}}]]]
Out[8]=

Compare with the result of using NSolve:

In[9]:=
x /. NSolve[ InterpolatingPolynomial[{{{-1}, 4, 0}, {{0}, 2, -3}, {1, 6}}, x], x]
Out[9]=

Properties and Relations (2) 

The dimensions of a Newton companion matrix might be much less than the number of points supplied:

In[10]:=
pts = {{-1, -4}, {-(2/3), -(107/27)}, {-(1/3), -(118/ 27)}, {0, -5}, {1/3, -(152/27)}, {2/3, -(163/27)}, {1, -6}}; ResourceFunction["NewtonCompanionMatrix"][pts] // MatrixForm
Out[10]=
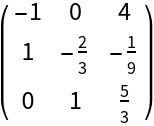
In[11]:=
Dimensions[%]
Out[11]=

In this case, the corresponding interpolating polynomial has degree 3:

In[12]:=
Expand[InterpolatingPolynomial[pts, x]]
Out[12]=

Version History

  • 1.0.0 – 26 April 2021

Source Metadata

  • Citation:
    • Calvetti D., Reichel L., Sgallari F., A modified companion matrix method based on Newton polynomials. In Fast algorithms for structured matrices: theory and applications, Contemporary Mathematics, vol. 323, 179-186. Providence, RI, American Mathematical Society, 2003.
      DOI: 10.1090/conm/323/05703
    • Corless R.M., Litt G., Generalized Companion Matrices for Polynomials not expressed in Monomial Bases. Ontario Research Centre for Computer Algebra, Technical Report, 2001.
      Available from http://kong.apmaths.uwo.ca/~rcorless/frames/PAPERS/PABV/CMP.pdf
    • Werner W., A generalized companion matrix of a polynomial and some applications. Linear Algebra and its Applications, vol. 55, 19-36, 1983.
      DOI: 10.1016/0024-3795(83)90164-7

Related Resources

License Information