Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 GeodesicSphereGraph

Source Notebook

Create a graph of an order-n geodesic sphere

Contributed by: Jan Mangaldan

ResourceFunction["GeodesicSphereGraph"][n]

gives a graph corresponding to an order-n geodesic sphere.

ResourceFunction["GeodesicSphereGraph"][base,n]

gives a graph corresponding to an order-n geodesic sphere based on the polyhedron base.

Details and Options

GeodesicSphereGraph[base, n] generates a three-dimensional graph corresponding to a geodesic sphere, also called a geodesic dome.
"Icosahedron" is the default value for base.
Possible values of base are "Tetrahedron", "Octahedron" or "Icosahedron".
GeodesicSphereGraph takes the same options as Graph3D.
With the setting VertexCoordinates→"Embedded", coordinates corresponding to the vertices of the geodesic sphere are generated with a special method.

Examples

Basic Examples (3) 

Generate an order-2 geodesic sphere:

In[1]:=
ResourceFunction["GeodesicSphereGraph"][2]
Out[1]=

Generate an order-2 geodesic sphere with specially computed coordinates:

In[2]:=
ResourceFunction["GeodesicSphereGraph"][2, VertexCoordinates -> "Embedded"]
Out[2]=

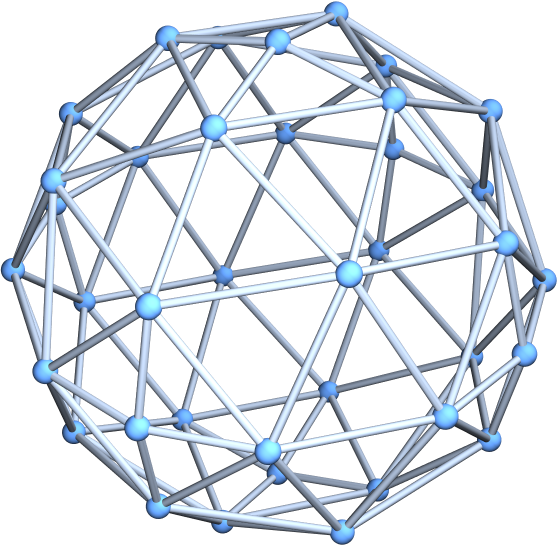
Generate an order-3 geodesic sphere with an octahedral base:

In[3]:=
ResourceFunction["GeodesicSphereGraph"]["Octahedron", 3, VertexCoordinates -> "Embedded"]
Out[3]=

Scope (2) 

Generate an icosahedral graph:

In[4]:=
ResourceFunction["GeodesicSphereGraph"][1, VertexCoordinates -> "Embedded"]
Out[4]=

Convert to a Graph object:

In[5]:=
ResourceFunction["GeodesicSphereGraph"][4] // Graph
Out[5]=

Options (4) 

GraphLayout (1) 

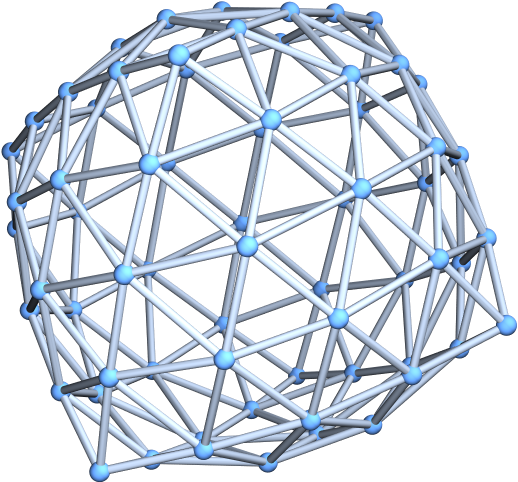
Specify various layouts for the geodesic sphere graph:

In[6]:=
ResourceFunction["GeodesicSphereGraph"]["Octahedron", 4, GraphLayout -> "SpringEmbedding"]
Out[6]=
In[7]:=
ResourceFunction["GeodesicSphereGraph"]["Octahedron", 4, GraphLayout -> "HighDimensionalEmbedding"]
Out[7]=

PlotTheme (1) 

Use a large graph theme:

In[8]:=
ResourceFunction["GeodesicSphereGraph"][4, PlotTheme -> "LargeGraph"]
Out[8]=

VertexCoordinates (2) 

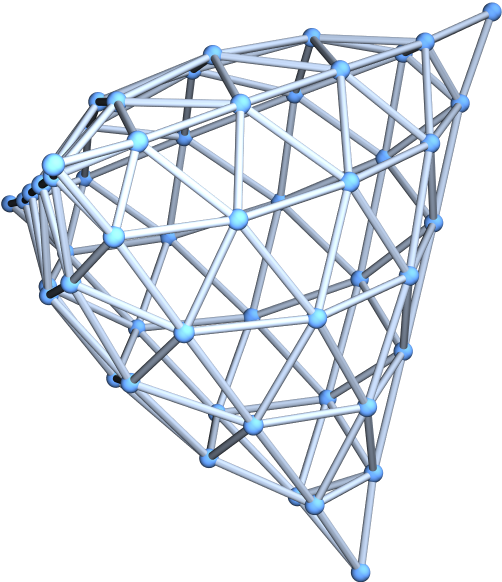
By default, vertex coordinates are computed automatically, depending on the setting for GraphLayout:

In[9]:=
ResourceFunction["GeodesicSphereGraph"]["Tetrahedron", 5]
Out[9]=

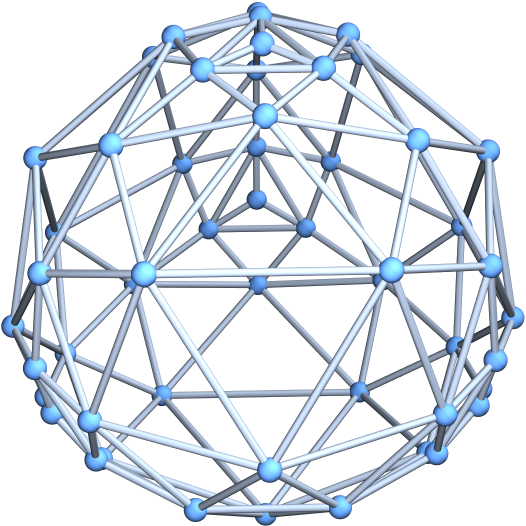
Use specially computed coordinates for the vertices:

In[10]:=
ResourceFunction["GeodesicSphereGraph"]["Tetrahedron", 5, VertexCoordinates -> "Embedded"]
Out[10]=

Version History

  • 1.0.0 – 02 March 2020

Related Resources

License Information