Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Convert a point reflected in a spherical mirror to its spherical anamorphosis map in a plane parallel to the xy-plane
ResourceFunction["SphericAnamorphosisMap"][{yi,zi},h] converts the point {0,yi,zi} inside a spherical mirror to its spherical anamorphosis map. |
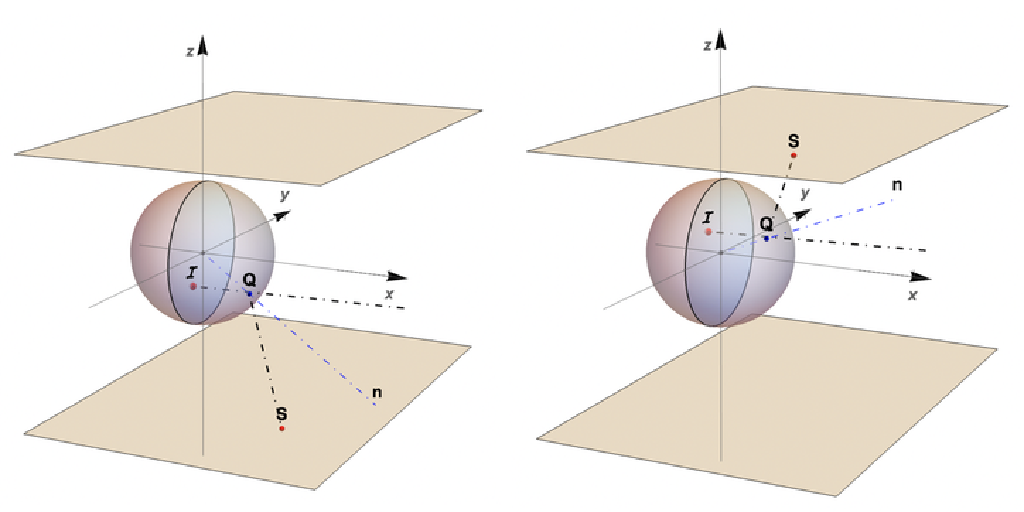
Get the anamorphic map in the plane z=2 of a point {-.15,.1} reflected in a spherical mirror:
| In[1]:= |
| Out[1]= |
Get the anamorphic map in the plane z=-2 of a point reflected in a spherical mirror as {-.15,-.1} in the yz-plane:
| In[2]:= |
| Out[2]= |
Points can be combined to form simple designs such as arrows:
| In[3]:= |  |
| In[4]:= |
| In[5]:= |
This 3D plot shows two arrows reflected in a spherical mirror and their anamorphic maps in the planes z=±2:
| In[6]:= | ![Graphics3D[{Thick, MapThread[{#1, Line@#2} &, {{Red, Blue}, {{arrowFloor, anaArrows[[1]]}, {arrowCeiling, anaArrows[[2]]}}}], Opacity[.35], Sphere[]}]](https://www.wolframcloud.com/obj/resourcesystem/images/7ef/7ef3203c-1e58-4262-bfb9-82f90c8514f6/7af13394bf34f3a1.png) |
| Out[6]= | 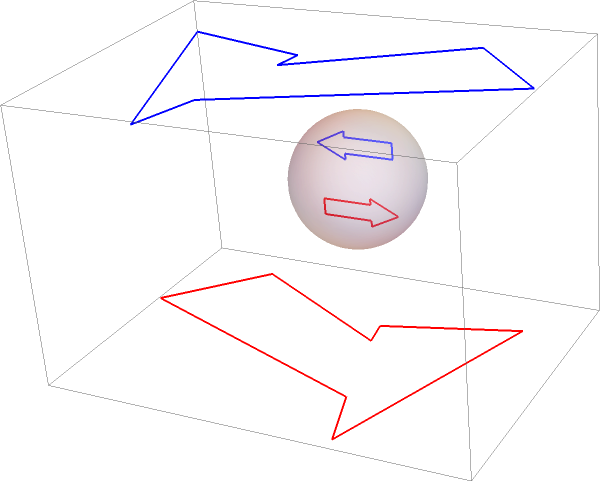 |
A classical example is a deformed anamorphic text message that can be reflected undeformed in a spherical mirror.
Convert a text into a set of point coordinates:
| In[7]:= | ![math = (First[
First[ImportString[
ExportString[
Style["\[Star]\[HeartSuit] I Love You \[HeartSuit]\[Star]",
FontFamily -> "Times", FontSize -> 72], "PDF"], {"PDF", "Pages"}, "TextMode" -> "Outlines"]]] /. FilledCurve :> JoinedCurve /. {x_?NumericQ, y_?NumericQ} :> {x, y}*.0047 /. {x_?NumericQ, y_?NumericQ} :> {x - .9, y - .40})[[-1, 1, All, -1]];](https://www.wolframcloud.com/obj/resourcesystem/images/7ef/7ef3203c-1e58-4262-bfb9-82f90c8514f6/609009ed6cbc10c7.png) |
After conversion of the point coordinates to their anamorphic map:
| In[8]:= |
| Out[9]= |  |
The sign of zi determines the sign of h or the location of the anamorphosis plane z=h:
| In[10]:= |
| Out[10]= |
Points with z-coordinates close to the equator z=0 have their anamorphosis map approaching infinity and should be avoided:
| In[11]:= |
| Out[11]= |
This work is licensed under a Creative Commons Attribution 4.0 International License