Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 AutomorphicIntegerQ

Source Notebook

Test whether an integer is automorphic in a given base or not

Contributed by: Naman Taggar

ResourceFunction["AutomorphicIntegerQ"][n,b]

returns True if n2 in a given base b ends in n, and False otherwise.

ResourceFunction["AutomorphicIntegerQ"][b]

represents an operator form of ResourceFunction["AutomorphicIntegerQ"] that can be applied to an integer.

Details

An integer is said to be automorphic in base b if (n2)b ends with n.
b is expected to be an integer greater than 1.
For negative integers n, n is considered automorphic in base b if Abs[n] is automorphic in base b.
ResourceFunction["AutomorphicIntegerQ"] threads over lists in n.

Examples

Basic Examples (2) 

5 is automorphic in base 10:

In[1]:=
ResourceFunction["AutomorphicIntegerQ"][5, 10]
Out[1]=

But 4 is not:

In[2]:=
ResourceFunction["AutomorphicIntegerQ"][4, 10]
Out[2]=

0 and 1 are automorphic in every base:

In[3]:=
AllTrue[Range[2, 100], And @@ ResourceFunction["AutomorphicIntegerQ"][{0, 1}, #] &]
Out[3]=

Scope (3) 

AutomorphicIntegerQ threads over a List:

In[4]:=
ResourceFunction["AutomorphicIntegerQ"][Range[10], 16]
Out[4]=

Using the operator form:

In[5]:=
ResourceFunction["AutomorphicIntegerQ"][6][Range[10]]
Out[5]=

A sequence of base-10 automorphic numbers is defined in OEIS:

In[6]:=
seq = ResourceFunction["OEISSequence"]["A003226"]
Out[6]=

Check it:

In[7]:=
ResourceFunction["AutomorphicIntegerQ"][seq, 10]
Out[7]=

Applications (1) 

Highlight the automorphic integers up to 100 in base 6:

In[8]:=
Multicolumn[ If[ResourceFunction["AutomorphicIntegerQ"][#, 6], Style[BaseForm[#, 6], Blue, Bold], BaseForm[#, 6]] & /@ Range[100], 10, Frame -> All, FrameStyle -> Gray]
Out[8]=

Properties and Relations (2) 

Anything except an integer for the first argument returns False:

In[9]:=
ResourceFunction["AutomorphicIntegerQ"][x, 1]
Out[9]=

Likewise any input besides an integer greater than 1 in the second argument yields False:

In[10]:=
ResourceFunction["AutomorphicIntegerQ"][10, 1]
Out[10]=
In[11]:=
ResourceFunction["AutomorphicIntegerQ"][x, 10]
Out[11]=

Publisher

Naman Taggar

Requirements

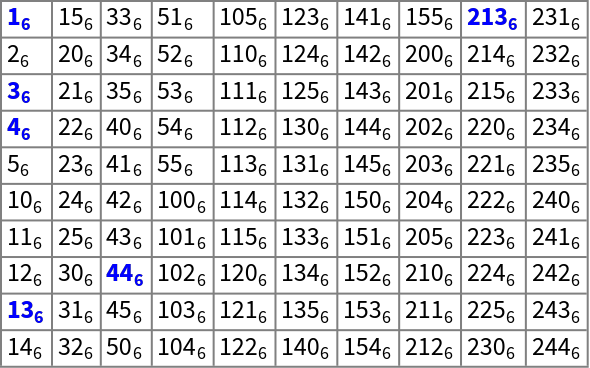Wolfram Language 14.0 (January 2024) or above

Version History

  • 1.0.0 – 09 July 2025

Related Resources

License Information