Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 FaurePoint

Source Notebook

Get a point belonging to the Faure sequence

Contributed by: Jan Mangaldan

ResourceFunction["FaurePoint"][k,d,b]

gives the kth d-dimensional point belonging to the base-b Faure sequence.

ResourceFunction["FaurePoint"][k,d]

automatically chooses the base.

Details

A Faure sequence is a quasirandom sequence (also called a low-discrepancy sequence) based on the permutation of a van der Corput sequence with a Pascal matrix.
The base should be a prime number greater than or equal to the dimension of the point.
ResourceFunction["FaurePoint"] gives a point belonging to the region [0,1]d.

Examples

Basic Examples (2) 

A 2D Faure point:

In[1]:=
ResourceFunction["FaurePoint"][10, 2]
Out[1]=

A 3D Faure point:

In[2]:=
ResourceFunction["FaurePoint"][10, 3]
Out[2]=

Scope (2) 

Use a different base:

In[3]:=
ResourceFunction["FaurePoint"][10, 3, 7]
Out[3]=

FaurePoint threads elementwise over lists:

In[4]:=
ResourceFunction["FaurePoint"][{17, 19, 23}, 3, 7]
Out[4]=

Applications (2) 

Show the structure of a Faure sequence in dimension 2:

In[5]:=
ListPlot[ResourceFunction["FaurePoint"][Range[0, 2^11 - 1], 2], AspectRatio -> 1, PlotStyle -> PointSize[Medium]]
Out[5]=

Use the Faure sequence to approximate π by quasi-Monte Carlo integration:

In[6]:=
With[{n = 2^13}, N[4 Mean[Boole[# . # <= 1] & /@ ResourceFunction["FaurePoint"][Range[0, n - 1], 2]]]]
Out[6]=

Properties and Relations (2) 

Use RescalingTransform to map Faure sequence points to other rectangular or cuboidal domains:

In[7]:=
Graphics3D[ Sphere[RescalingTransform[ ConstantArray[{0, 1}, 3], {{1, 3}, {-1, 1}, {0, 2}}][ ResourceFunction["FaurePoint"][Range[0, 3^7 - 1], 3]], 0.02]]
Out[7]=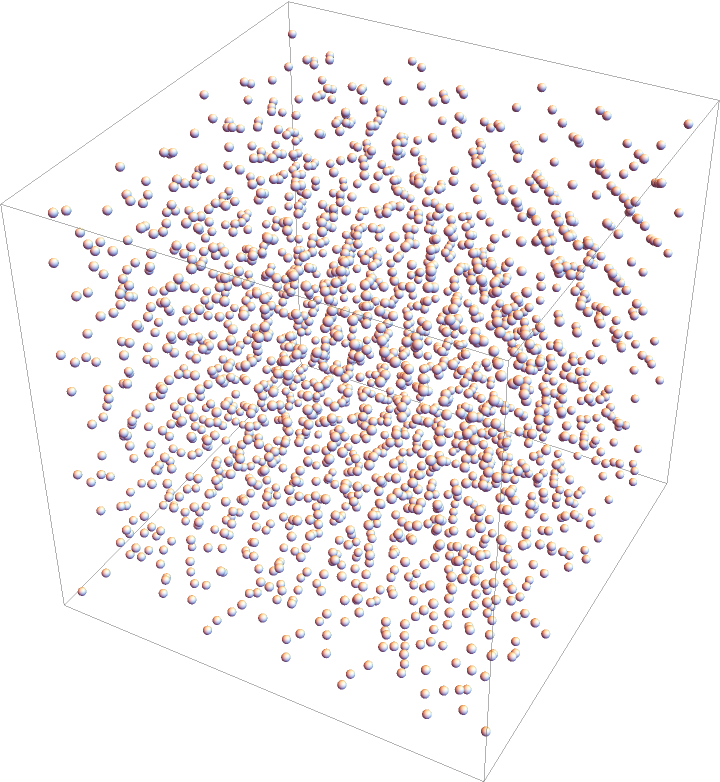

If the unit square is divided into rectangles with area b-n, each rectangle contains exactly one member of the first bn points generated by the base b Faure sequence:

In[8]:=
With[{b = 2, n = 8, p = 4, q = 4}, ListPlot[ResourceFunction["FaurePoint"][Range[0, b^n - 1], 2, b], AspectRatio -> 1, GridLines -> {Subdivide[b^p], Subdivide[b^q]}, GridLinesStyle -> Directive[AbsoluteThickness[2]], PlotRange -> {{0, 1}, {0, 1}}, PlotStyle -> AbsolutePointSize[2]]]
Out[8]=

Version History

  • 1.0.0 – 01 June 2021

Source Metadata

  • Citation:
    • Faure H., "Discrépance de suites associées à un système de numération (en dimension s). Acta Arithmetica, vol. 41, no. 4, 337–351, 1982. http://eudml.org/doc/205851
    • Faure H., "Using permutations to reduce discrepancy." Journal of Computational and Applied Mathematics, vol. 31, no. 1, 97–103, 1990. DOI: 10.1016/0377-0427(90)90340-6

Related Resources

Author Notes

Scrambling and other enhancements to Faure's original method will be added at a later date.

License Information